目录
二、排序算法(承接第一部分)
1、堆排序算法——树的基础知识补充
2、树的基本概念
3、二叉树基础知识
(1)满二叉树
(2)完全二叉树
(3)二叉树的存储方式(表示方式)
4、堆排序(大根堆、小根堆)
(1)堆排序过程
(2)构造堆
(3)挨个出数
5、堆排序——内置模块
6、堆排序应用——topk问题
二、排序算法(承接第一部分)
1、堆排序算法——树的基础知识补充
- 树是一种数据结构 比如:目录结构
- 树是一种可以递归定义的数据结构
- 树是由n个节点组成的集合
- 如果n=0,那这是一颗空树
- 如果n>0,那存在一个节点作为树的根节点,其他节点可以分为m个集合,每隔几何本身又是一棵树
2、树的基本概念
- 根节点、叶子结点(例如:B、C、H、P、Q等 不能分叉的节点)
- 树的深度(高度):最深有几层,图中为4
- 树的度(整个树,最大节点的度)、节点的度(F的度为3,分了3个叉)
- 孩子节点(子节点)、父节点(E为I的父节点、I为E的孩子节点)
- 子树
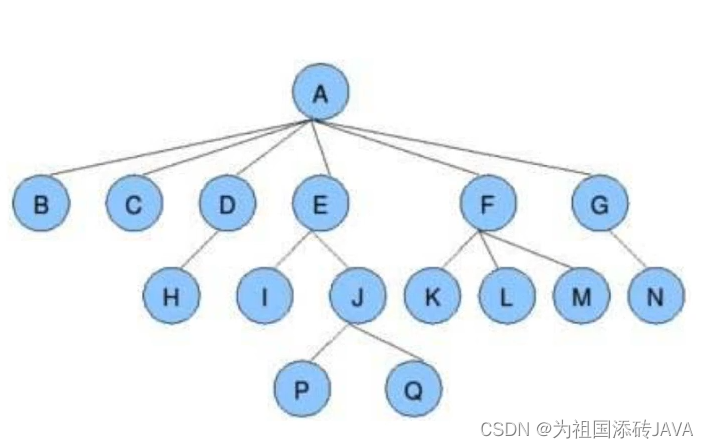
3、二叉树基础知识
- 度不超过2的树
- 每个节点最多有两个孩子节点
- 两个孩子节点被区分为左孩子节点和右孩子节点
(1)满二叉树
- 一个二叉树,如果每一个层的节点数都达到最大值,则这个二叉树就是满二叉树
(2)完全二叉树
- 叶节点只能出现在最下层和次下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树
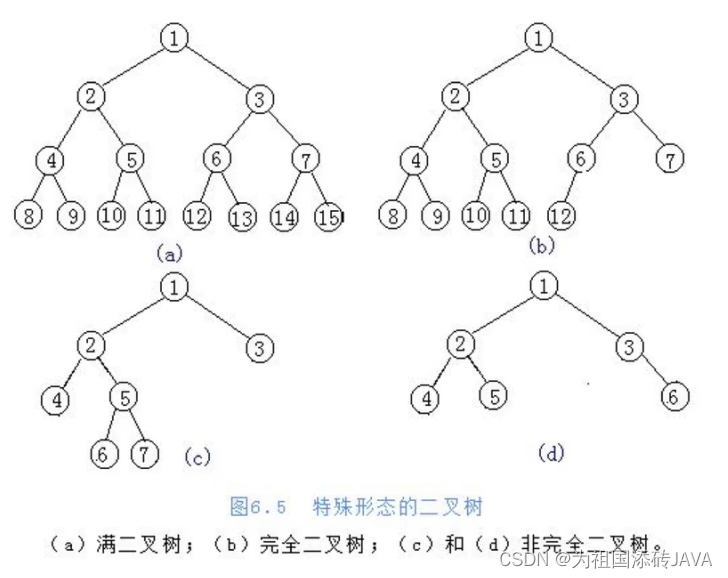
(3)二叉树的存储方式(表示方式)
- 链式存储
- 顺序存储(堆排序)
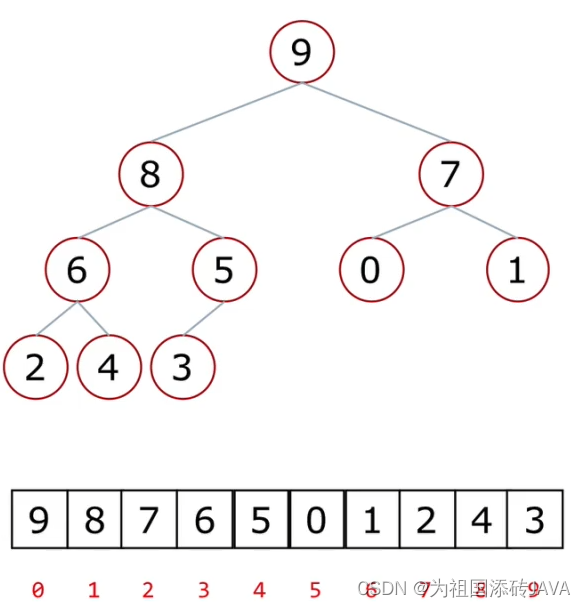
从图中我们需要找到两个问题:
- 父节点和左孩子节点的编号下标有什么关系?
- 0-1 1-3 2-5 3-7 4-9
- i - 2i+1
- 父节点和右孩子节点的编号下标有什么关系?
- 0-2 1-4 2-6 3-8 4-10
- i - 2i+2
4、堆排序(大根堆、小根堆)
- 堆:一种特殊的完全二叉树结构
- 大根堆:一颗完全二叉树,满足任一节点都比其他孩子节点大
- 小根堆:一颗完全二叉树,满足任一节点都比其他孩子节点小
- 复杂度O(nlogn)

(1)堆排序过程
- 建立堆(构造堆)
- 得到堆顶元素,为最大元素
- 去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整(向下调整)使堆有序
- 堆顶元素为第二大元素
- 重复步骤3,直到堆变空
Note:
如果不是取最后一个元素到堆顶,再进行向下调整,将会导致不是完全二叉树
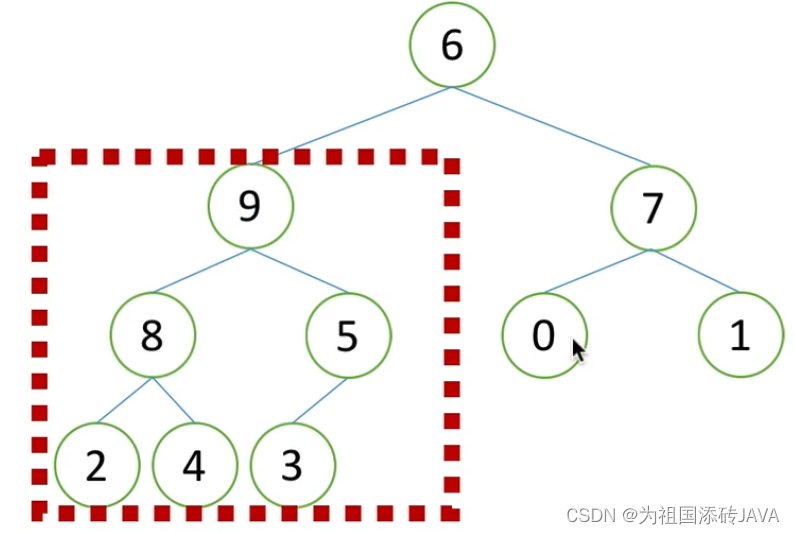
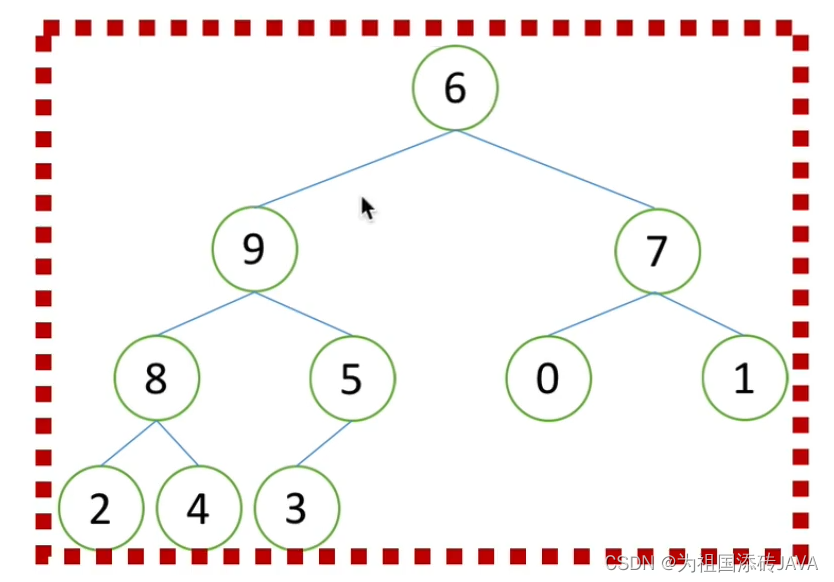
(2)构造堆
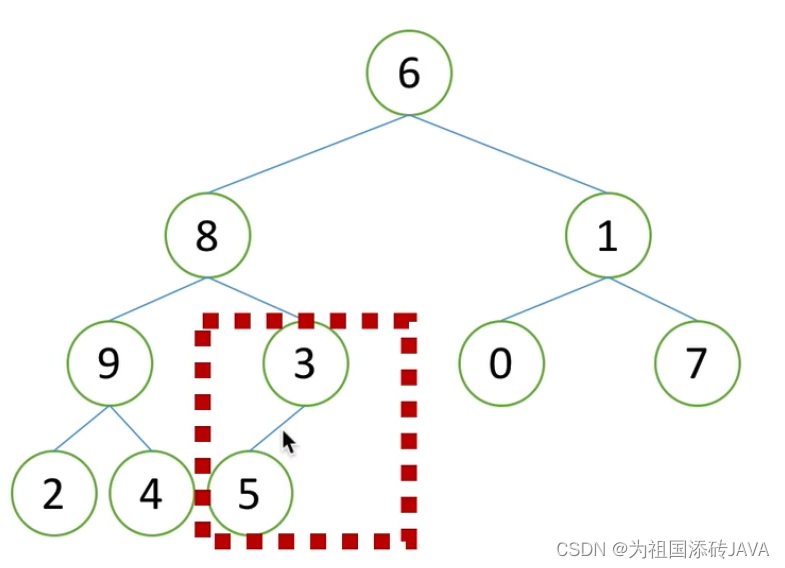
先对最后一个非叶子节点进行调整
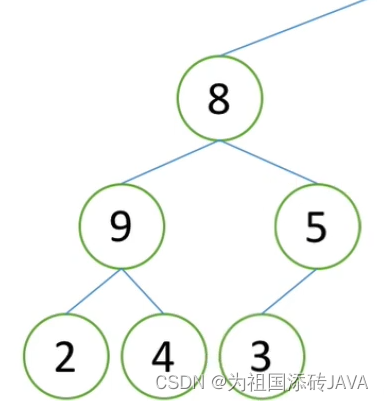
然后依次继续往上进行调整
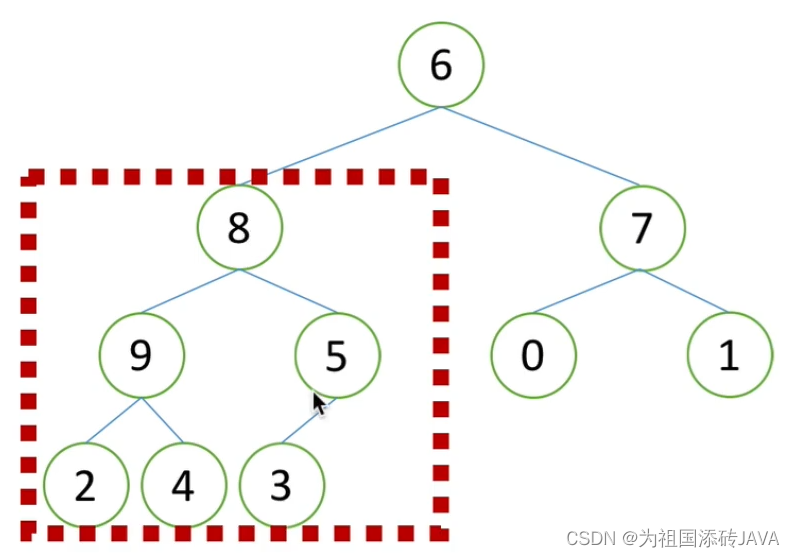
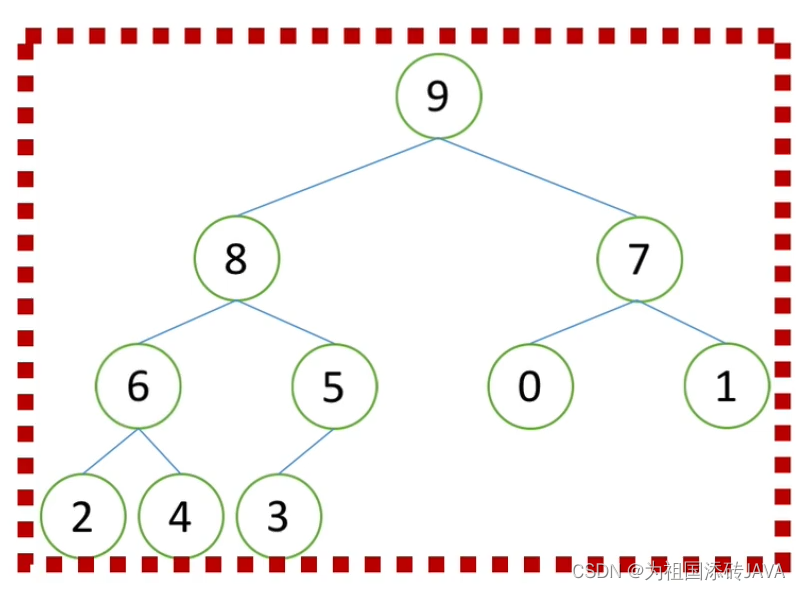
(3)挨个出数
当堆构造好之后,在进行挨个出数
import random
import numpy as np
def sift(li, low, high):
'''
:param li: 列表
:param low: 堆的第一个元素 (根)
:param high: 堆的最后一个元素
'''
i = low # 此时i指向第一层
j = 2 * i + 1 # 左孩子
temp = li[low] # 暂存堆顶元素
while j <= high: # 只要j没有超过high
# 有右孩子且与左孩子对比 (j + 1 <= high )表示右孩子没有越界
if j + 1 <= high and li[j + 1] > li[j]:
j = j + 1 # j指向右孩子
if temp < li[j]:
li[i] = li[j]
i = j # 往下走一层
j = 2 * i + 1
else: # temp更大
li[i] = temp # 把temp放到某一层根部
break
else:
li[i] = temp # temp不在根节点,跳出循环后,temp放到叶子结点处
def head_sort(li):
# 首先建堆
n = len(li)
# 寻找父亲节点 i-1//2 i=n-1
for i in range((n - 2) // 2, -1, -1):
# i 表示建堆的时候调整的部分根的下标
sift(li, i, n - 1)
# 建堆完成
for i in range(n - 1, -1, -1):
# i指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0] # 堆顶元素和最后一个元素调整
sift(li, 0, i - 1) # 调整 (此时最后一个元素是i-1)
li = [i for i in range(100)]
random.shuffle(li)
print(li)
head_sort(li)
print(li)
5、堆排序——内置模块
- Python内置模块——heapq(q:queue 优先队列)
- 常用函数
- heapify(x)(建堆——小根堆)
- heappush(heap,item)(往里面加元素)
- heappop(heap)往外弹出一个元素(最小的元素)
import heapq
import random
li = [i for i in range(100)]
random.shuffle(li)
print(li)
heapq.heapify(li)
print(li)
for i in range(100):
print(heapq.heappop(li), end=',')6、堆排序应用——topk问题
- 现在有n个数,设计算法得到前k大的数。(k<n)
- 解决思路:
- 排序后切片 O(nlogn)
- 冒泡、插入、选择排序O(kn)
- 堆排序 O(nlogk)
- 取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行一次调整。
- 遍历列表所有元素后,倒序弹出堆顶
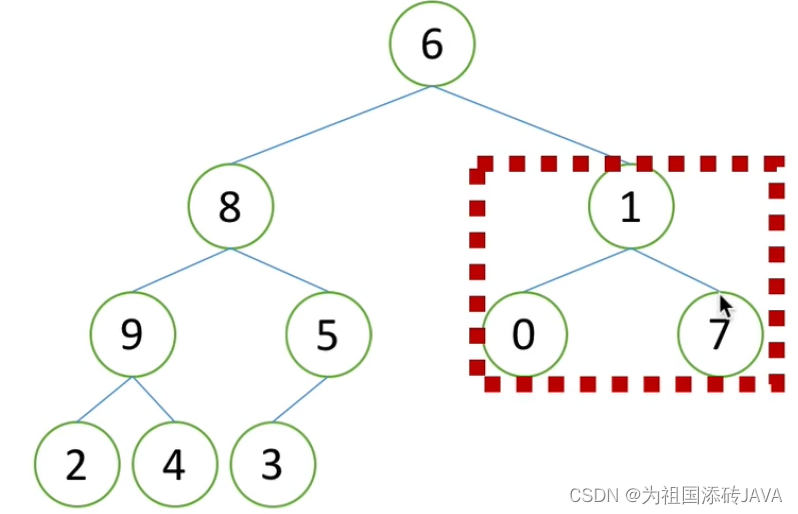
例如:我们想到找到前5大的数字,我们先取前五个数字建立一个小根堆

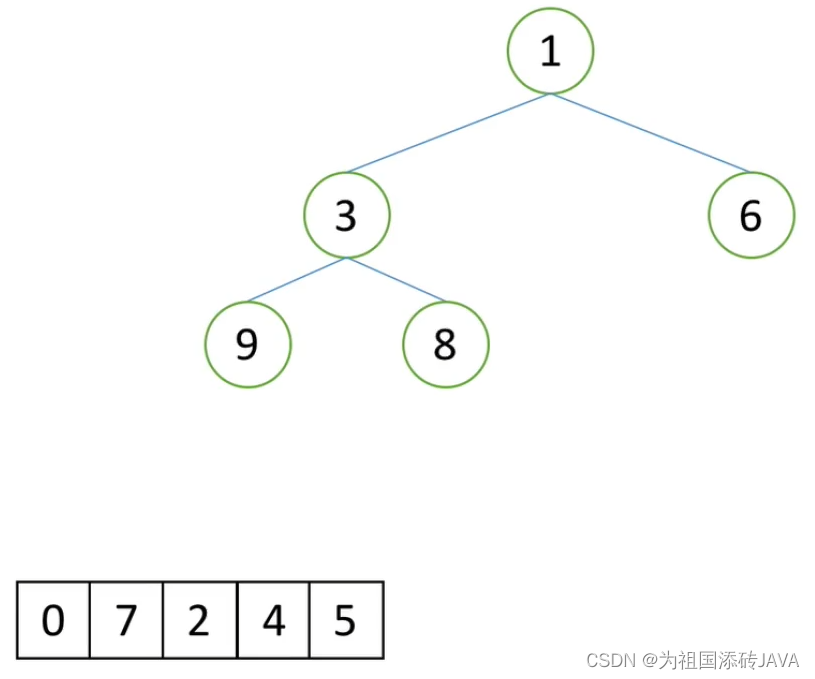
发现0不能放进去,只剩下7、2、4、5
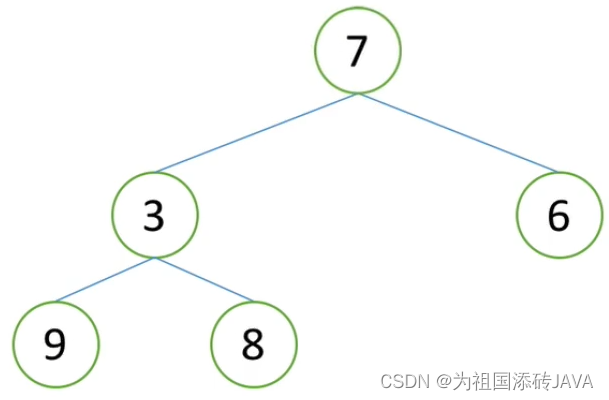
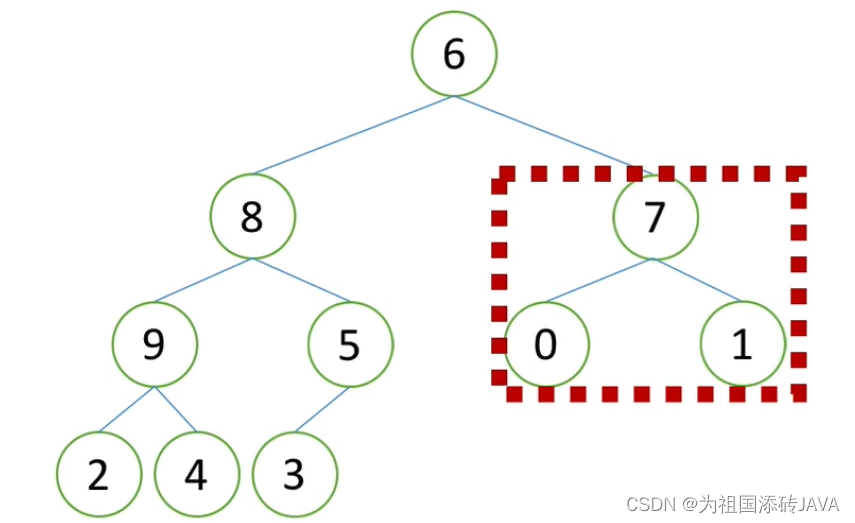
7比1大,所以把1换掉,在进行小根堆调整

以此类推,最后
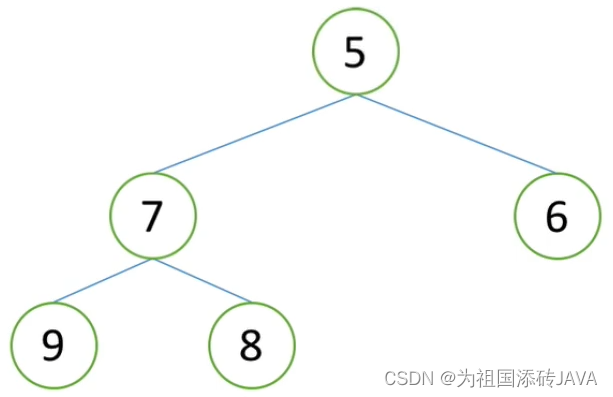
import random
def sift(li, low, high):
'''
:param li: 列表
:param low: 堆的第一个元素 (根)
:param high: 堆的最后一个元素
'''
i = low # i,j指向层
j = 2 * i + 1 # 左孩子
temp = li[low] # 暂存堆顶元素
while j <= high: # 只要j没有超过high
# 有右孩子且与左孩子对比 (j + 1 <= high )表示右孩子没有越界
if j + 1 <= high and li[j + 1] < li[j]:
j = j + 1 # j指向右孩子
if temp > li[j]:
li[i] = li[j]
i = j
j = 2 * i + 1
else:
li[i] = temp # 把temp放到某一层根部
break
else:
li[i] = temp # temp不在根节点,跳出循环后,temp放到叶子结点处
def topK(li, k):
'''前k个元素'''
heap = li[0:k]
for i in range(k - 2 // 2, -1, -1):
sift(heap, i, k - 1)
# 1.建堆
for i in range(k, len(li) - 1):
if li[i] > heap[0]:
heap[0] = li[i]
sift(heap, 0, k - 1)
# 2.遍历
for i in range(k - 1, -1, -1):
heap[0], heap[i] = heap[i], heap[0]
sift(heap, 0, i - 1)
# 3.返回前k个
return heap
if __name__ == '__main__':
li = [i for i in range(100)]
print(li)
random.shuffle(li)
print(li)
print(topK(li, 10))