Netlogo学习笔记

第一行：国际惯例咕咕咕。

第二行：人工势场这个概念好神奇（虽然我觉得就是强行捏了一个高大上的词

第三行：希望全天下的软件都能把要用的东西集成成库，然后只需要无脑点点就可以了（我本人：又懒又馋还不爱劳动（武林外传十娘皱眉苦瓜脸.jpg

第四行：所有代码注释：不知道netlogo该怎么写注释就按python来了【upd：我知道了用“;;”来注释但是懒得改了】

第五行：netlogo的语法就是所有的东西都得空格隔开，3*9也得写成3 * 9

第六行：我要开始自行编辑了

一、安装+初步认识

这本书真好使，简单明了容易上手：《Netlogo多主体建模入门》

话不多说官网走起：netlogo下载链接

~~（实验室15kb的网速支持我摸鱼）（老师你看这可不怪我是网不行）（我超会找借口der）~~

1.1 生命游戏

具体规则：略(好多不想打上，反正就是小方格中的黑白色块在周8个邻居的相互作用下变黑变白的过程)

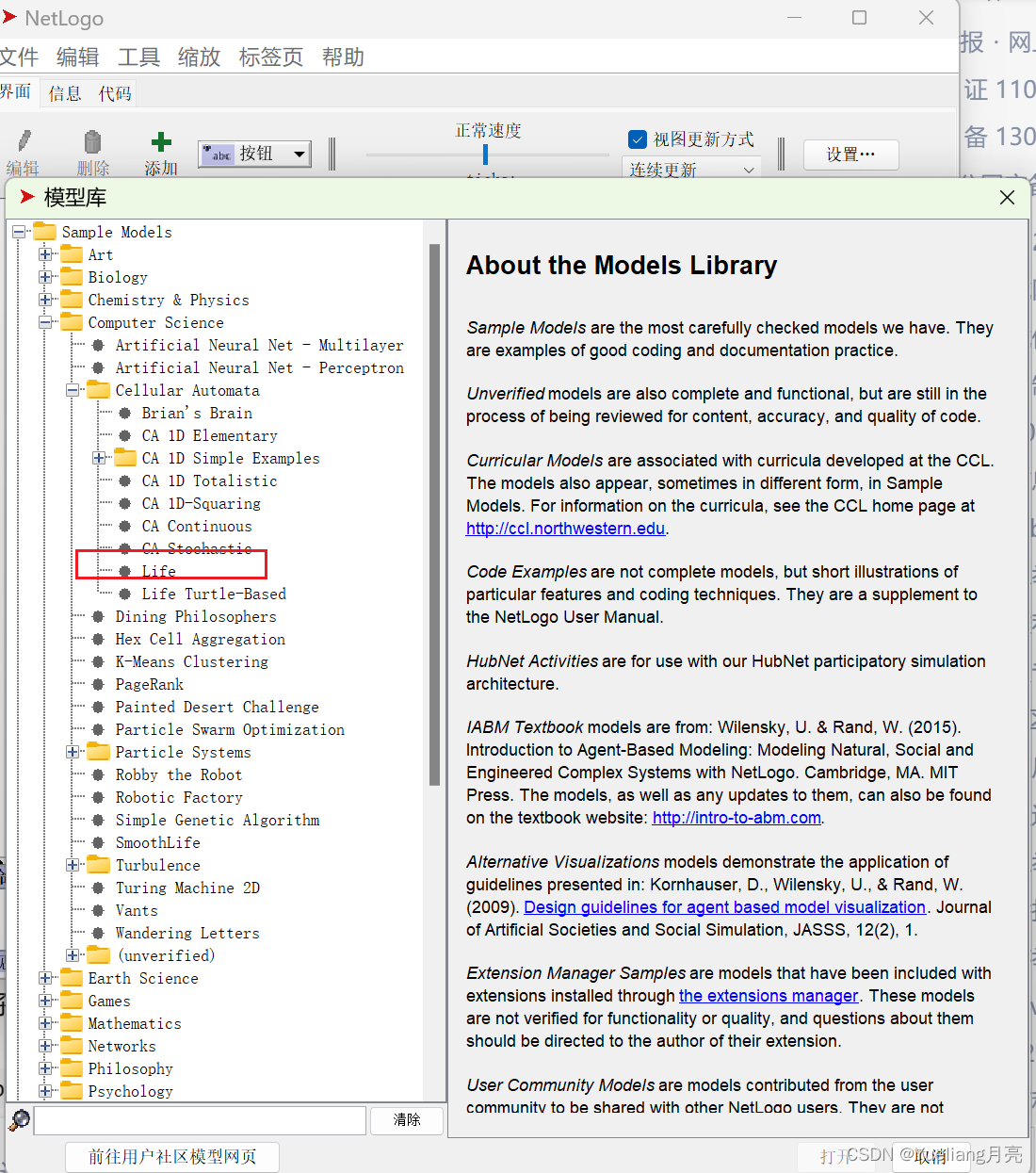
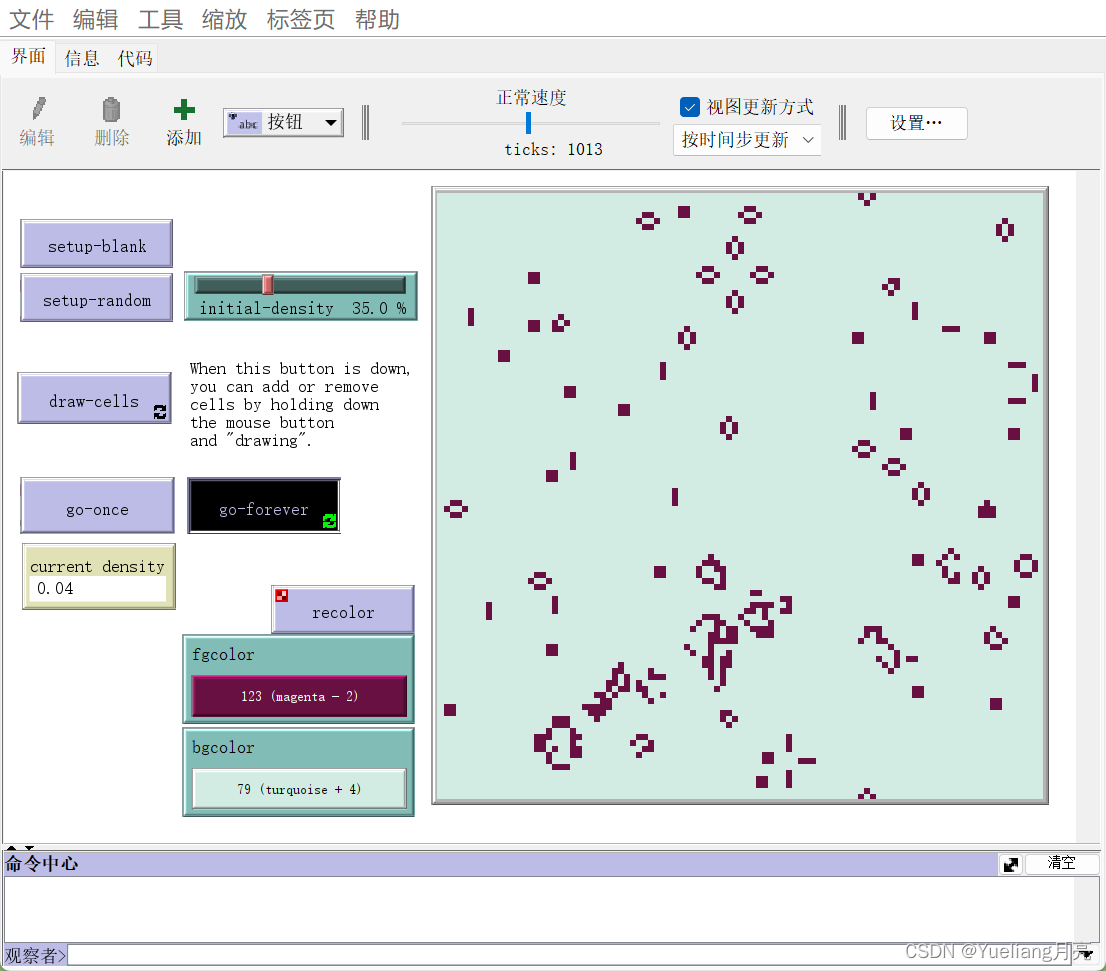
步骤：新建项目：文件->模型库->life（左图）；setup-random：初始化（中图）；go-forever：最终结果（右图）

结果：最终会形成小方格中黑白色块的死亡or存活图

1.2 鸟群模型

具体规则：略（模拟鸟群靠近or远离其他鸟，且保持飞行方向的过程）

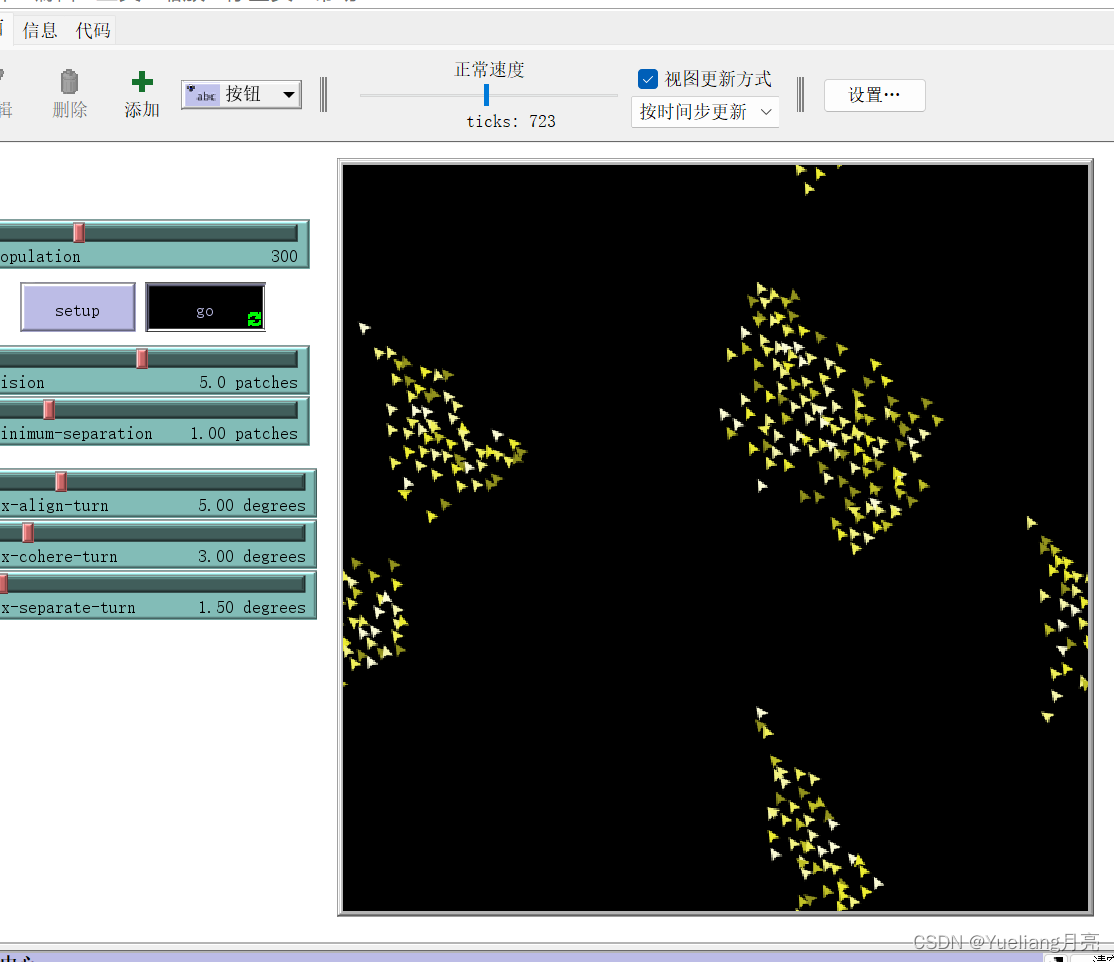
步骤：新建项目：文件->模型库->bioligy（左图）；setup+go（右图）

结果：最终可以看到鸟群成群一起往某个方向飞并且鸟群没有发生碰撞

1.3 财富分布模型

具体规则：略（更麻烦了，分谷物和人的分布，人：采集谷物+消耗谷物+代谢不同+可能饿死+新出生，谷物：生长）

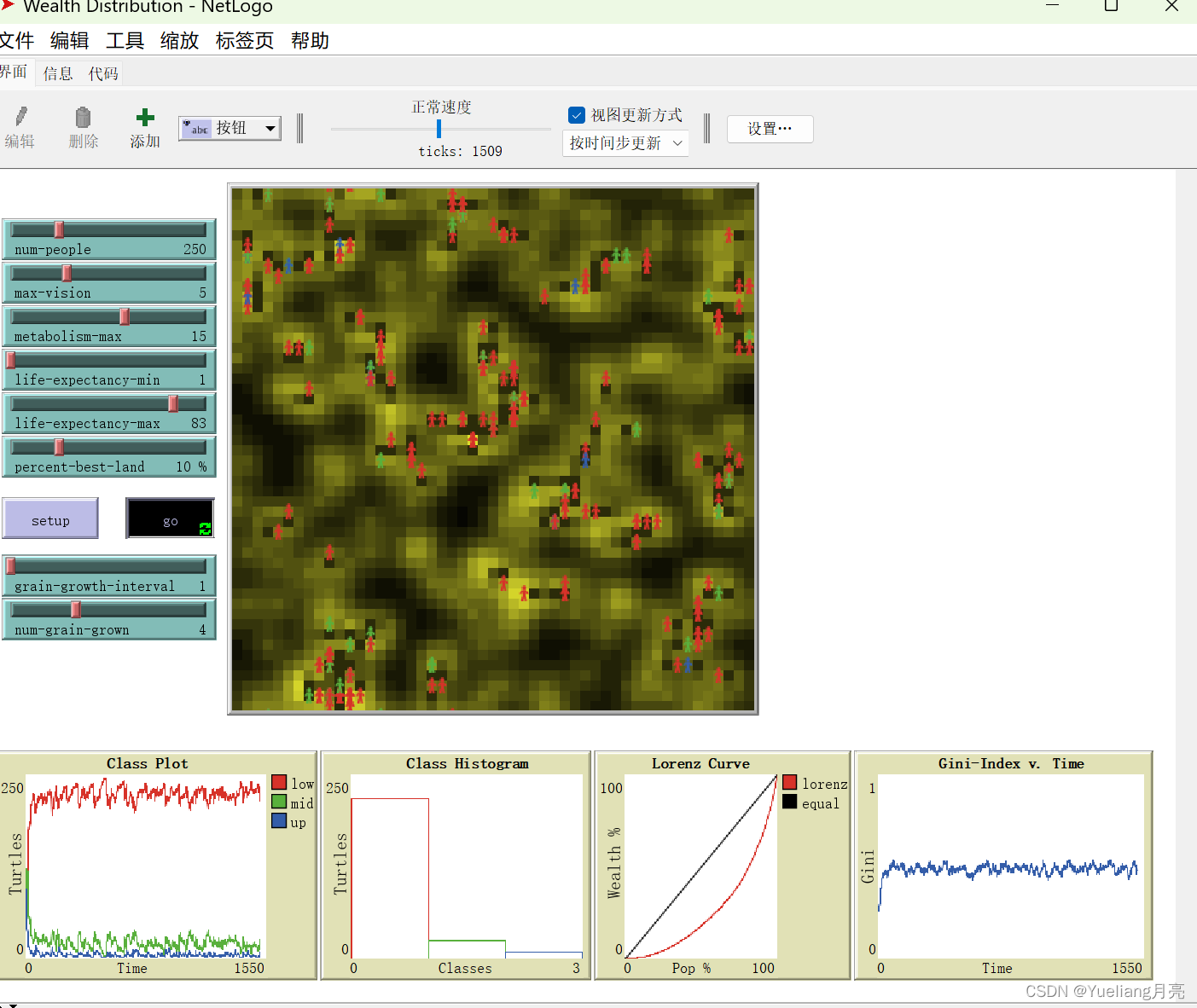
步骤：文件->模型库->ScocialSicence.Economics.Sugarscape（左图）；set-go（右图）

结果：class plot+class histogram：展示穷人、中产、富人的数量对比(可以看出二八定律)；Lorenz curve(洛伦兹曲线)：反映财富分配不均衡现象(红线越弯曲不均衡程度越高)；Gini-Index(基尼系数)：国际通用衡量财富不均衡的指标，数值越大越不均衡(一般0.3/0.4左右)

二、正式上手

此部分中都有各自的规则（~~但是由于我懒，我就不写了~~

2.1 小球宇宙

本模型：随机出现，单步移动

学习：对语法集合等有个初步认识

添加按钮并对按钮命名，右键黑色世界后编辑可对模拟世界的属性进行修改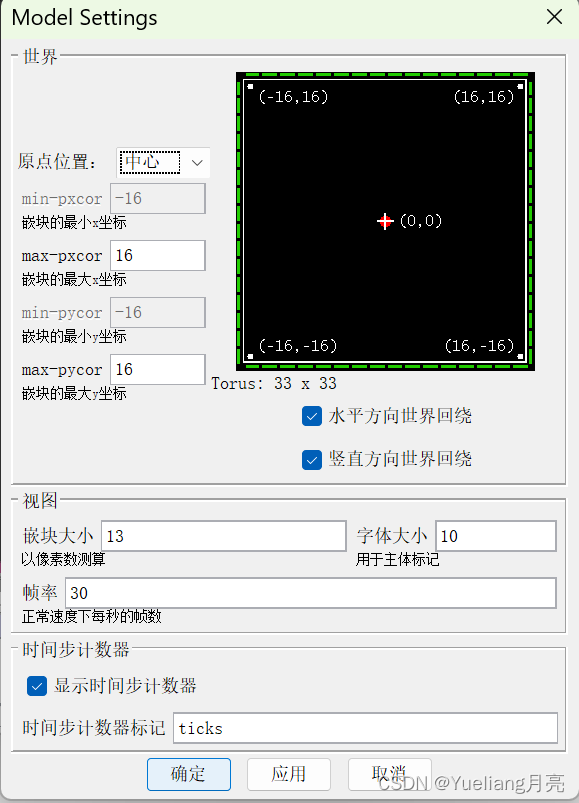，在代码模块中编写代码对按钮进行设置

#对setup按钮进行设置
to setup
  clear-all #每次运行清空屏幕
    set-default-shape turtles "circle" #设置形状为圆形
  create-turtles 50[
    setxy random-xcor random-ycor #50个小球且setxy随机横纵坐标
    ]
end
#对go按钮进行设置
to go
  ask turtles[ #ask相当于循环，对turtles这个集合进行下面操作的循环
    forward 1 #每点一次小球前进一个位置
  ]
end

效果图（左：setup，右：go）：

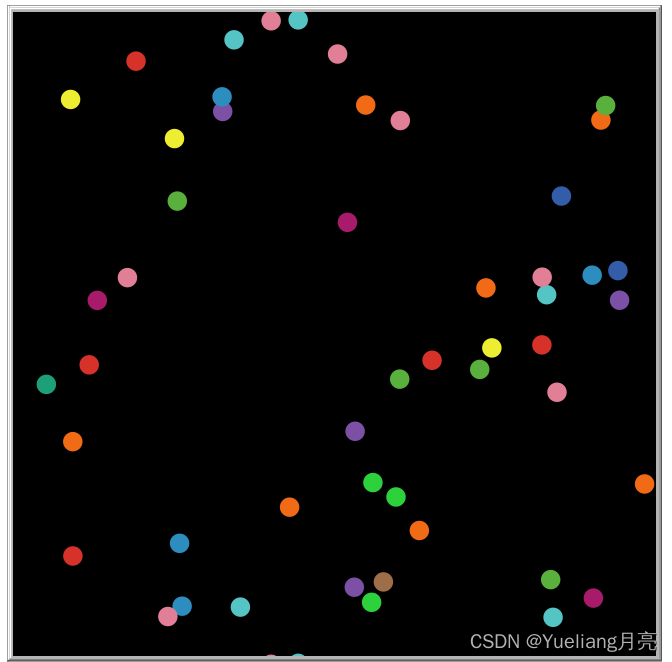
2.2 生命游戏

本模型：被邻居影响而改变

学习要求：对集合+patch有进一步的概念，掌握set命名变量、条件语句、with筛选集合，会调整model和patch的大小

模拟世界本质由许多patch组成（可以理解为n*n的像素矩阵），所以可以对ptach进行属性设定，利用patch的颜色设置来模拟生命游戏

16*16的世界+13的patch

50*50的世界+4的patch

patches-own [living] #设置变量名为living的patch（本质为一个集合
to setup
  clear-all
  ask patches[ #对这个集合内的变量进行循环
    if random-float 1 < 0.3[ #此命令产生一个小于1的0-1之间的数，并用if判断产生的数是否小于0.3
      set pcolor white #设置变量pcolor为白色
    ]
    set living 0 #设置变量living为0
  ]
end

to go
  ask patches[
    set living count neighbors with [pcolor = black] 
#对每个patch设置living变量为计算周围8个patch中为黑色的数量
#count为自带计数函数
#neighbors为保留字（构成集合
#with也为保留字（后跟限定条件来筛选集合
  ]
  ask patches[
    ifelse (pcolor = black)[ #ifelse条件语句，注意格式为ifelse[条件1][条件2]
      if living > 3 or living < 2[
        set pcolor white  
      ]      
     ][
        if (living = 3)[
          set pcolor black
        ]
      ]
    ]
end

2.3 朗顿的蚂蚁

本模型：主体和环境不停地相互影响并发生改变

学习要求：学习random函数，掌握时间计数方式（设置更新按时间步更新）

（左图的中心其实是有一个patch的（像素太小了可能看不出来（但是不调大小就看不出蚂蚁修路来（bushi（很神奇的是1w时间步左右开始修路后面就不修了成一个花点点了

to setup
  clear-all
  reset-ticks #ticks用来计时
  create-turtles 1[ #生成了一个turtle
    set heading random 3 * 90 #设置的是turtle的朝向，随机生成四个方向
#这句的本质是heading((random 3)*90)即随机生成一个小于3的非负整数后再乘90，即只会生成0，90，180，270四种
  ]
end

to go
  ask turtles[
    ifelse (pcolor = white)[
      right 90 #向右转90°，其实相当于是head = head+90
      set pcolor black
      forward 1
    ][
      left 90 #向左转90°，同理，head-90
      set pcolor white
      forward 1
    ]
  ]
  tick
end

2.5 羊草生态系统

本模型：两种不同的主体相互影响作用，草被吃也生长，羊吃草也繁衍也死亡

学习要求：自定义函数的使用、智能主体的监控、如何绘图

左图：setup后绿色为草，红色为羊右图：一段时间后被吃的草和繁衍的羊

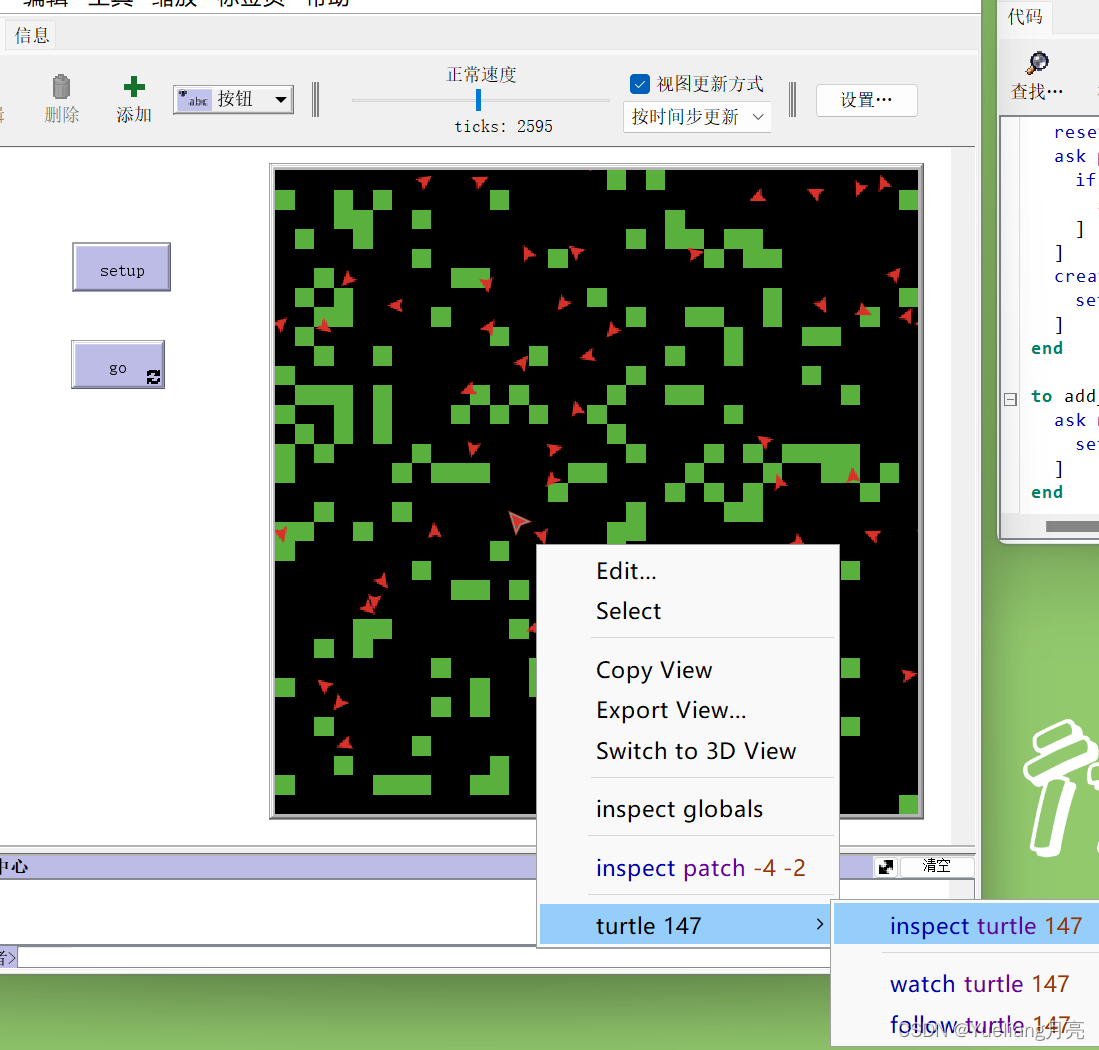
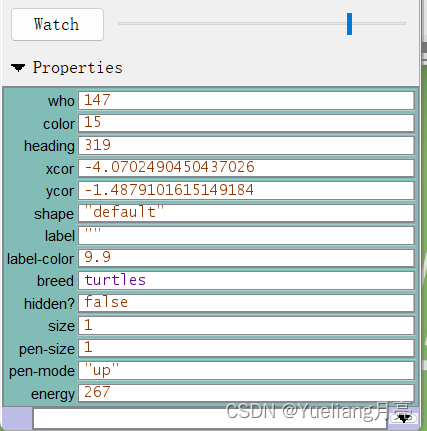
左图：右键patch后可以观察其具体右图：能看到的具体属性

左图：添加绘图按钮后并进行绘图右图：运行一段时间后（可以看出这是一个典型的捕食者-被捕食者模型，绿色代表草，一开始很多，黑色代表羊一开始很少，短期内羊大量繁殖，草急剧减少，过了一段时间会达到一个相对平衡的状态）

turtles-own [energy] #同样设置了一个变量
to setup
  clear-all
  reset-ticks
  ask patches[
    if random-float 1 < 0.2[
      set pcolor green
    ]
  ]
  create-turtles 1[
    set energy 100  #设置该变量的初始值为100
  ]
end
#草增加函数
to add_food
  ask n-of 10 patches[
#n-of函数的作用是从patches集合中随机挑选10个patch形成一个新的集合
    set pcolor green
  ]
end
#羊移动函数
to turtle_move
  if pcolor = green[
    set energy energy + 10 #羊移动会吃草，增加自身能量，但是草会没有
    set pcolor black
  ]
  if random-float 1 < 0.2[
    set heading random 360 #设定概率让羊随机转换方向移动
  ]
  set energy energy - 1 #每次移动都会消耗自身能量
  fd 1 #forward缩写，即移动
end
#羊繁衍
to turtle_breed
  if energy > 500[
    set energy energy - 500 #大于500就生小羊，自身能量减少
    hatch 1[
      fd 1
      set energy 100 #新羊的能量100，前移1格
    ]
  ]
end
#羊死亡
to turtle_die
  if energy <= 0[
    die
  ]
end

to go
  add_food #草不停增加
  ask turtles[ #羊不停移动+吃草+繁衍+死亡
    turtle_move
    turtle_breed
    turtle_die
  ]
  tick
end

三、进阶开始

3.1 人工经济模型

本模型：财富分配的表示（交易过程中的财富聚集）

学习要求：了解set和let的区别（let 和 set都可以对变量进行赋值，不同的是let可以赋值未定义的变量，set只能赋值前面定义过的变量）；注意变量的作用域；对绘图进行设置（可进行画笔的设置来画直方图or条形图等）；用滑块来控制变量数；使用工具-行为空间-新建实验做重复实验；在观察中心设置命令进行实验

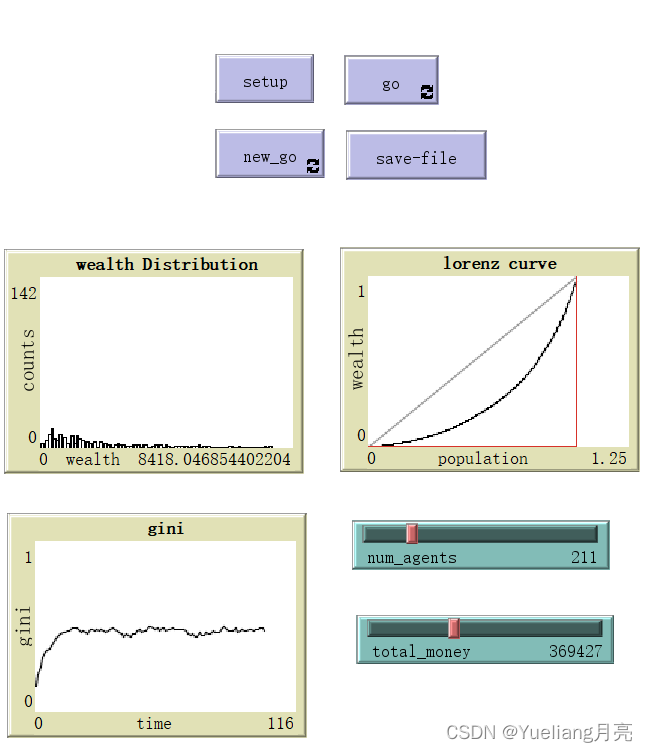
#设置变量（利用滑块设置的全局变量）
turtles-own[
  money #每个主体有的钱数
  save_rate #储蓄率
]
to setup
  clear-all
  reset-ticks
  create-turtles num_agents[
    set money (total_money / num_agents) #钱=总/人数
    setxy random-xcor random-ycor
    set save_rate random-float 1 #随机的储蓄率
  ]
end

to transaction [trader] #[]中是传入的变量
  let deltam 0 #货币转移量，初值为0
  let money1 ([money] of trader) #存储传入变量的值
  let epsilon (random-float 1) #0~1的随机数
  set deltam (epsilon - 1) * money + epsilon * money1 #设置交易量
  if money + deltam >= 0 and money1 - deltam >= 0[ #不允许借贷，交易货币总量不低于0才会交易
    set money money + deltam
    ask trader[
      set money money1 - deltam
    ]
  ]
end

to go
  ask turtles[
    let agsets other turtles-here #对每个变量进行赋值，turtle-here返回的是潜在交易对象
#当前patch上除了自身外的所有turtle，是一个集合
    if count agsets >= 1[
      transaction (one-of agsets) #大于等于1就发生交易，one-of从集合中随机选择元素
    ]
    forward 1
  ]
  tick
end

#新的交易中引入了储蓄率有的人并不会全部进行交易
to transaction_new [trader]
  let deltam 0
  let money0 ((1 - save_rate) * money)
  let money1 ((1 - ([save_rate] of trader)) * ([money] of trader))
  let epsilon (random-float 1)
  set deltam (epsilon - 1) * money0 + epsilon * money1
  if money + deltam >= 0 and ([money] of trader) - deltam >= 0[
    set money money + deltam
    ask trader[
      set money money - deltam
    ]
  ]
end

to new_go
  ask turtles[
    let agsets other turtles-here
    if count agsets >= 1[
      transaction_new (one-of agsets)
    ]
    forward 1
  ]
  tick
end

to to-update-plot
  let lst [money] of turtles #是一个集合，每个turtle的财富值
  set-histogram-num-bars 100 #统计小区间的个数为100
  if not empty? lst[
    set-plot-x-range 0 max lst #设置x轴的范围
    histogram lst #绘制直方图
  ]
end

to save-file
  file-open "agents.txt" #打开一个txt文件（会自行生成
  let wealths ""
  ask turtles[
    set wealths (word wealths money "\r\n") #word 数值 数值，对wealth进行赋值
  ]
  file-print wealths #写入文件
  file-close
end

to update-lorenz-plot
  clear-plot
#绘制表示财富分布绝对均衡的曲线
  set-current-plot-pen "equal" #激活画笔
  plot 0 #设置纵坐标，横坐标等水平间隔
  plot 1
#极端不平衡的曲线
  set-current-plot-pen "dominant"
  plot-pen-down #开始绘图
  plotxy 0 0 #设置xy点
  plotxy 1 0
  plotxy 1 1
  plot-pen-up #停止绘图
#洛伦兹曲线（根据洛伦兹的规则来的）
  set-current-plot-pen "lorenz"
  set-plot-pen-interval 1 / num_agents #设置间隔量
  plot 0
  let sorted-wealths sort [money] of turtles #
  let total-wealth sum sorted-wealths
  let wealth-sum-so-far 0
  let index 0
  let gini 0
  
  repeat num_agents[
    set wealth-sum-so-far(wealth-sum-so-far + item index sorted-wealths)
    plot(wealth-sum-so-far / total-wealth)
    set index (index + 1) 
    set gini gini + ((index / num_agents) - (wealth-sum-so-far / total-wealth)) / num_agents
  ]
  set-current-plot "gini" #基尼系数
  plot gini * 2
end

to-report compute-gini
  let sorted-wealths sort [money] of turtles
  let total-wealth sum sorted-wealths
  let wealth-sum-so-far 0
  let index 0
  let gini 0
  repeat num_agents[
    set wealth-sum-so-far (wealth-sum-so-far + item index sorted-wealths)
    plot (wealth-sum-so-far / total-wealth)
    set index (index + 1)
    set gini gini + ((index / num_agents) - (wealth-sum-so-far / total-wealth)) / num_agents
  ]
  set-current-plot "gini"
  report gini * 2
end

3.2 人工鸟群

本模型：鸟的跟随or远离（鸟的视野半径+靠近规则+对齐规则+分离规则）

学习要求：掌握矢量的加减法、数乘；list的使用；map来对整个列表进行作用

（注意：因为书中没有给出变量的设置，所以不同的数值会影响不同的靠近对齐等，可自行进行修改调整）

turtles-own[
  velocity flockingmates colisionmates
] #设置了速度矢量+靠近范围的所有邻居+分离范围的所有邻居（是集合

to setup
  clear-all
  crt num_boids[
    setxy random-xcor random-ycor
    set velocity [0 0] #是一个速度矢量，用二元列表实现
    set size 3
  ]
end

to go
  ask turtles[ #first和last用来取列表的最初和最后元素
    get-neighbors #获取每只鸟的邻居，包括靠近范围内的邻居和分离范围内的邻居
    flocking #根据Boids的3条规则，计算所有的力并更新速度
    facexy xcor + (first velocity) ycor + (last velocity) #设定鸟的朝向为其速度矢量
    setxy xcor + (first velocity) ycor + (last velocity) #设定下一时刻的位置
  ]
end

to get-neighbors #设置了分离半径和视野半径
  set flockingmates (other turtles in-radius viewdistance) #获得veditance距离内的所有其他岛
  set colisionmates (other turtles in-radius collisiondistance) #获得cosoindisie距离内的
end

to flocking
  let corr [0 0] #所有邻居的平均位置
  let v[0 0] #所有邻居的平均速度
  let cn count flockingmates #邻居的数量，count为自带函数
  ask flockingmates[ #map可以运算列表中的所有元素
    set corr (map + corr (list xcor ycor)) #对列表中的所有元素进行+xcor ycor
    set v (map + v velocity) #全加velocity
  ]
  if cn > 0[ #?表示形式化的参数，?1 ?2表示第一二个参数，?表示所有参数(可以理解为：f(x,y)等)
    set corr (map[ ?1 -> ?1 / cn ] corr) #corr中的所有元素都除以cn
    set v (map[ ?1 -> ?1 / cn ] v) #v中的每个元素都除以cn
  ]
  let dis(map - corr (list xcor ycor)) #dis= Corr -XCOr, ycOr,从“我”的位
  set cn count colisionmates
  let cdis [0 0]
  if cn > 0[
    let ccorr [0 0]
    ask colisionmates[
      set ccorr (map + ccorr (list xcor ycor))
  ]
    set ccorr (map[ ?1 -> ?1 / cn] ccorr)
    set cdis (map - (list xcor ycor) ccorr)
    set cdis (map [?1 -> ?1 / ((norm cdis)*(norm cdis) + 0.001) ] cdis)
  ]
  let w1 weight_cohesion
  let w2 weight_alignment
  let w3 weight_collision
  let f1 (map [ ?1 -> ?1 * w1 ] dis)
  let f2 (map[ ?1 -> ?1 * w2] v)
  let f3 (map[ ?1 -> ?1 * W3 ] cdis)
  let force (map [[?1 ?2 ?3] -> ?1 + ?2 + ?3] f1 f2 f3)
  set velocity (map + velocity force)
  if (norm velocity) > 5[
    set velocity normalize velocity
    set velocity map [?1 -> ?1 * 5] velocity
  ]
end

to-report normalize [xy] #进行归一化处理
  let realdis norm xy
  let out [0 0]
  if realdis > 0[
    set out (map [ ?1 -> ?1 / realdis ] xy)
  ]
  report out
end

to-report norm [arr] #计算矢量的模，传入的是列表arr
  let xx first arr
  let yy last arr
  report sqrt (xx * xx + yy * yy)
end