前期准备

数据准备

数据集有两个表

1. 销售数据表
2. 投放费用的广告费用表

文章源码获取方式 👉👉 点击文末名片

1. 分别按 日 和 月 分析销售收入

绘制子图

figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None,frameon=True)
	num:图像编号或名称．数字为编号，字符串为名称
    figsize:指定figure的宽和高．单位为英寸
    dpi参数指定绘图对象的分辨率，即每英寸多少个像素，缺省值为80 1英寸等于2.5cm,A4纸是21*30cm的纸张
	facecolor:背景颜色
	edgecolor:边框颜色
	frameon:是否显示边框

(1 ) subplot语法
subplot(nrows,ncols,sharex,sharey,subplot_kw.**fig_kw)

nrows       subplot的行数
ncols       subplot的列数
sharex      所有subplot应该使用相同的X轴刻度.(调节xlim将会影响所有subplot)
sharey      所有subplot应该使用相同的Y轴刻度（调节ylim将会影响所有subplot)
subplot_kw  用于创建各subplot的关键字字典
**fig_kw    创建figure时的其他关键字，如plt.subplots(2,2,figsize=(8,6))

import pandas as pd
import matplotlib.pyplot as plt

pd.set_option('display.unicode.east_asian_width', True) 


df = pd.read_excel('.\data\销售表.xlsx')  
df = df[['日期', '销售码洋']]  
df['日期'] = pd.to_datetime(df['日期'])  
df1 = df.set_index('日期')  
df_d = df1.resample('D').sum().to_period('D')  
df_d.to_excel(r'.\result\result1.xlsx')  

df_m = df1.resample('M').sum().to_period('M')  
df_m.to_excel(r'.\result\result2.xlsx')  

plt.rc('font', family='SimHei', size=10) 

fig = plt.figure(figsize=(9, 5)) 
ax = fig.subplots(1, 2) 

ax[0].set_title('按日分析销售收入')  # 设置图表标题
df_d.plot(kind='line', ax=ax[0], color='r')  

ax[1].set_title('按月分析销售收入')  # 设置图表标题
df_m.plot(kind='bar', ax=ax[1], color='g') 

plt.subplots_adjust(top=0.95, bottom=0.18)  
plt.savefig(r'.\result\01_sales.png')  # 保存图片
plt.show()

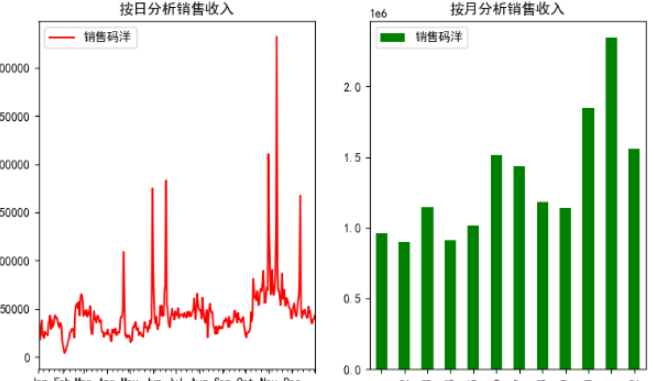
接着我们开始研究投放的广告费用与销量存在的相关关系，
如果相关度高，

我们即可以利用广告费用来预测销售量。

2. 按月份分析广告费用与销售收入

import pandas as pd
import matplotlib.pyplot as plt
源码领取+wx：xiaoyuanllsll
df1 = pd.read_excel('.\data\广告费.xlsx')
df2 = pd.read_excel('.\data\销售表.xlsx')

df2 = df2[['日期', '销售码洋']]  
# 将日期转换为日期格式
df1['投放日期'] = pd.to_datetime(df1['投放日期'])
df2['日期'] = pd.to_datetime(df2['日期'])
df1 = df1.set_index('投放日期') 
df2 = df2.set_index('日期')  

df_y1 = df1.resample('M').sum().to_period('M')  # 按月统计广告费
df_y2 = df2.resample('M').sum().to_period('M')  # 按月统计销售码洋

y1 = pd.DataFrame(df_y1['支出'])  # 广告费支出
y2 = pd.DataFrame(df_y2['销售码洋'])  # 销售码洋

plt.rc('font', family='SimHei', size=10)  

fig = plt.figure() 
ax1 = fig.add_subplot(111)  

plt.title('京东电商销售收入与广告费分析折线图')  

x_ticks = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]   
x_label = ['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月', '12月'] 
plt.xticks(x_ticks, x_label) 

ax1.plot(x_ticks, y1, color='orangered', linewidth=2, linestyle='-', marker='o', mfc='w', label='广告费')


plt.legend(loc='upper left')  

ax2 = ax1.twinx() 
ax2.plot(x_ticks, y2, color='g', linewidth=2, linestyle='-', marker='o', mfc='w', label='销售收入')
plt.legend(loc='upper center')  

plt.subplots_adjust(right=0.85)  
plt.savefig(r'.\result\02_line.png') 
plt.show()

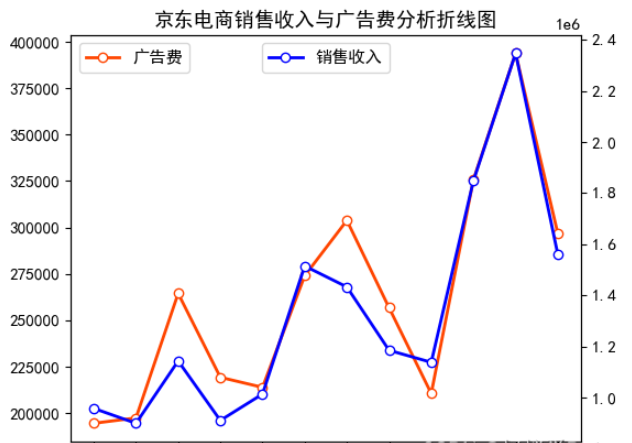
从上图我们可以发现广告费和销量收入的走势基本相同，
下面我们还可以通过广告费用与销量收入的散点图来验证。

3. 广告费用与销量收入之间的散点图

import pandas as pd
import matplotlib.pyplot as plt

df1 = pd.read_excel('.\data\广告费.xlsx')
df2 = pd.read_excel('.\data\销售表.xlsx')

df2 = df2[['日期', '销售码洋']]  

df1['投放日期'] = pd.to_datetime(df1['投放日期'])
df2['日期'] = pd.to_datetime(df2['日期'])

df1 = df1.set_index('投放日期', drop=True)
df2 = df2.set_index('日期', drop=True)
df_x = df1.resample('M').sum().to_period('M')
df_y = df2.resample('M').sum().to_period('M')

x = pd.DataFrame(df_x['支出'])
y = pd.DataFrame(df_y['销售码洋'])

plt.rc('font', family='SimHei', size=11)  
plt.figure("京东电商销售收入与广告费分析散点图")  
plt.scatter(x, y, color='r')  
plt.xlabel('广告费（元）')  
plt.ylabel('销售收入（元）')
plt.subplots_adjust(left=0.15)  
plt.savefig(r'.\result\03_scatter.png')  
plt.show()

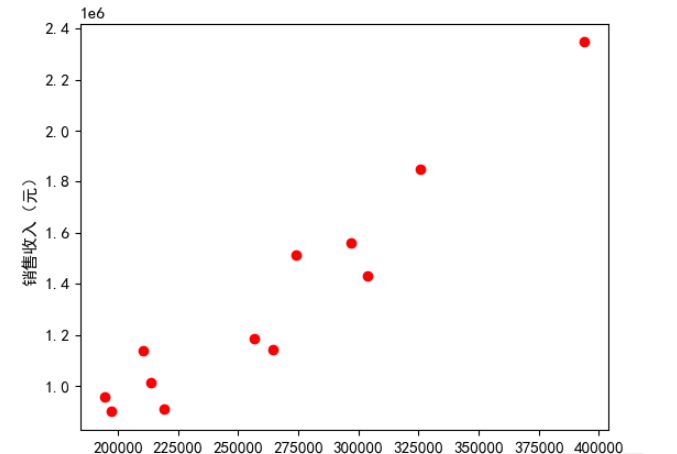
我们发现，

两者的确在一个线条区域上，

可以基本判别两者存在相关关系。

接下来我们就可以利用

线性回归方程

通过投放的广告费用来预测销售收入。

4. 线性回归方程通过投放的广告费用来预测销售收入

import pandas as pd
from sklearn import linear_model
import matplotlib.pyplot as plt
import numpy as np

df1 = pd.read_excel('.\data\广告费.xlsx')
df2 = pd.read_excel('.\data\销售表.xlsx')

df2 = df2[['日期', '销售码洋']]  
df1['投放日期'] = pd.to_datetime(df1['投放日期']) 
df2['日期'] = pd.to_datetime(df2['日期']) 

df1 = df1.set_index('投放日期', drop=True) 
df2 = df2.set_index('日期', drop=True) 
df_x = df1.resample('M').sum().to_period('M')
df_y = df2.resample('M').sum().to_period('M')

x = pd.DataFrame(df_x['支出'])
y = pd.DataFrame(df_y['销售码洋'])

clf = linear_model.LinearRegression() 
clf.fit(x, y)
k = clf.coef_  
b = clf.intercept_ 
print('回归系数k:', k, '截距b：', b)

x0 = np.array([120000, 130000, 150000, 180000, 200000, 250000])
x0 = x0.reshape(6, 1) 
y0 = clf.predict(x0)
print('预测销售收入：')
print(y0)

y_pred = clf.predict(x)

plt.rc('font', family='SimHei', size=11)  
plt.figure("京东电商销售数据分析与预测")
plt.scatter(x, y, color='r') 
plt.plot(x, y_pred, color='blue', linewidth=1.5) 
plt.xlabel('广告费（元）')  
plt.ylabel('销售收入（元）')
plt.subplots_adjust(left=0.15)  
plt.savefig(r'.\result\04_pred.png')  
plt.show()

from sklearn.metrics import r2_score

y_true = [360000, 450000, 600000, 800000, 920000, 1300000]  
score = r2_score(y_true, y0)  
print("预测评分")
print(score)

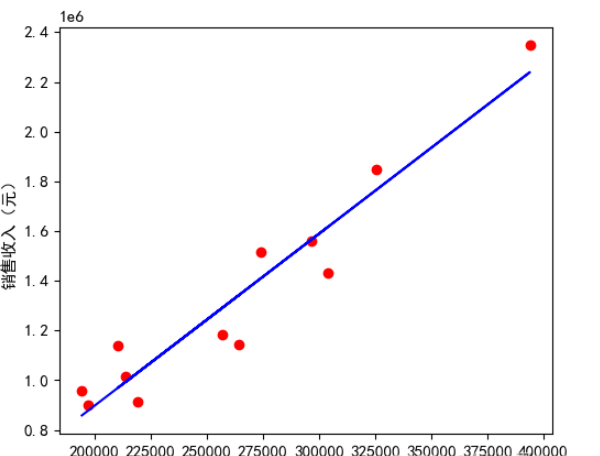
回归系数k: [[6.92235616]] 截距b： [-487521.71147034]
预测销售收入：
[[ 343161.02820353]
 [ 412384.58984301]
 [ 550831.71312199]
 [ 758502.39804046]
 [ 896949.52131943]
 [1243067.32951688]]
预测评分
0.9839200886906196

总结

最后我们对算法进行检验，
验证该算法的有效性。

利用带标签的数据，
与回归方程的预测值作比较。
常用的损失函数为：MSE（误差平方和）
最后得分为 0.9839200886906198（得分，也可做准确率）

说明这回归方程还是预测效果很好的。