博主简介：想进大厂的打工人
博主主页：@xyk:
所属专栏: 笔试强训专栏

笔试强训

文章目录

一、选择题

1.1 10.1.0.1/17的广播地址是（）

1.2 网络地址172.16.22.38/28 请写出此地址的子网ID以及广播地址，此地址所处子网可用主

机数

1.3 tcp三次握手的过程，accept发生在三次握手哪个阶段

1.4 Linux中，一个端口能够接受tcp链接数量的理论上限是（D）

1.5 随着IP网络的发展，为了节省可分配的注册IP地址，有一些地址被拿出来用于私有IP地址，以下不属于私有IP地址范围的是（C）

1.6 下面是一个http请求：

二、[编程题]左右最值最大差

三、OR38 顺时针打印矩阵

一、选择题

1.1 10.1.0.1/17的广播地址是（）

A.10.1.128.255
B.10.1.63.255
C.10.1.127.255
D.10.1.126.255

解：10.1.0.1/17

17代表的是子网掩码：前面17个 1代表网络号，后面15个0代表主机号

广播地址就是：主机号全为1；

所以，32为位IP地址，前17位为 10.1.0.1的前17位，后15位为1

10.1.0.1/17化为二进制为 00001010 00000001 00000000 00000001后15为全为1

即为：

00001010 00000001 01111111 11111111 就是10.1.127.255

1.2 网络地址172.16.22.38/28 请写出此地址的子网ID以及广播地址，此地址所处子网可用主机数

A.172.16.22.32 172.16.22.255 12
B.172.16.22.32 172.16.22.47 16
C.172.16.22.32 172.16.22.255 15
D.172.16.22.32 172.16.22.47 14

解

1、172.16.22.38/28表示：IP地址+子网掩码地址

（1）其中172.16.22.38为IP地址：172.16.22.0010 0110

（2）其中“/28“表示子网掩码，或者说表示子网掩码的前28位都是1，其他位为0;

即子网掩码为： 1111 1111，1111 1111， 1111 1111， 1111 0000；

=> 255，255，255，240；

2、子网掩码：255.255.255.1111 0000；IP地址：172.16.22.0010 0110

IP地址和子网掩码进行“与运算”得子网ID：

（255.255.255.1111 0000）&（172.16.22.0010 0110）= 172.16.22.0010 0000；

即：子网ID为：172.16.22.32

3、32 - 28 = 4，子网最多有 2的4次方个： 2^4 = 16个。

主机地址：172.16.22.0010 0000；=>172.16.22.32；（可用位全为0）

广播地址：172.16.22.0010 1111；=>172.16.22.47；（可用位全为1）

实际可用主机数：16 - 2 = 14个；（去除主机地址和广播地址，剩下一个主机分一个地址）；

1.3 tcp三次握手的过程，accept发生在三次握手哪个阶段

A 第一次握手
B 第二次握手
C 第三次握手
D 三次握手后

第一次握手：客户端发送syn包(syn=j)到服务器。
第二次握手：服务器收到syn包，必须确认客户的SYN（ack=j+1），同时自己也发送一个ASK包（ask=k）。
第三次握手：客户端收到服务器的SYN＋ACK包，向服务器发送确认包ACK(ack=k+1)。
三次握手完成后，客户端和服务器就建立了tcp连接。这时可以调用accept函数获得此连接

1.4 Linux中，一个端口能够接受tcp链接数量的理论上限是（D）

A 1024
B 65535
C 65535 * 65535
D 无上限

tcp链接数量的理论上限跟端口没有关系；对于服务端来说一个客户端的连接请求到来，创建一个新连接，新连接源端地址与监听连接绑定地址相同，只是对端地址不同，描述通信两端的信息，跟端口没有关系，所以理论上并没有限制，全凭主机的资源上限

1.5 随着IP网络的发展，为了节省可分配的注册IP地址，有一些地址被拿出来用于私有IP地址，以下不属于私有IP地址范围的是（C）

A 10.6.207.84
B 172.23.30.28
C 172.32.50.80
D 192.168.1.100

用于组建私网的网段有：10.*网段和172.16.* ~ 172.31.*网段以及192.168.*网段

1.6 下面是一个http请求：

GET /baidu/blog/item/6605d1b4eb6433738ad4b26d.html HTTP/1.1 
Host: hi.baidu.com 
User-Agent: Mozilla/5.0 (Windows; U; Windows NT 5.1; zh-CN; rv:1.8.0.6) Gecko/20060728 Firefox/1.5.0.6 
Accept: text/xml,application/xml,application/xhtml+xml,text/html;q=0.9,text/plain;q=0.8,image/png,*/*;q=0.5 
Accept-Language: zh-cn,zh;q=0.5 
Accept-Encoding: gzip,deflate 
Accept-Charset: gb2312,utf-8;q=0.7,*;q=0.7 
Keep-Alive: 300 
Connection: keep-alive 
Referer: http://hi.baidu.com/baidu 
Cookie: BAIDUID=AFB70E986AC48B336ABAB7505CDD1C76; 
下面关于 Host、User-Agent、Accept-Charset、Connection、Referer、Cookie描述错误的是？

A.Host:HTTP服务器的IF地址或者域名
B.User-Agent:告诉HTTP服务器，客户端使用的操作系统和浏览器的名称和版本.
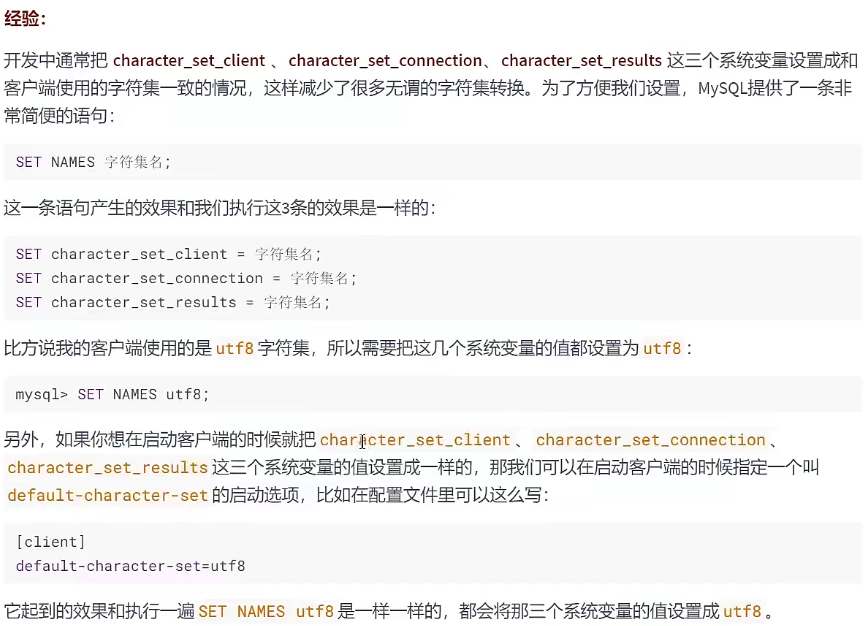
c.Accept-Charset:浏览器申明自己接收的字符集，这就是本文前面介绍的各种字符集和字符编码，如gb2312，utf-8
D.cookie:它记录了服务器的相关的一些信息
E.Referer:提供了Request的上下文信息的服务器，告诉服务器我是从哪个链接过来的

cookie是用来记录用户信息，表明用户身份的

二、[编程题]左右最值最大差

链接：左右最值最大差__牛客网
来源：牛客网

给定一个长度为N(N>1)的整型数组A，可以将A划分成左右两个部分，左部分A[0..K]，右部分A[K+1..N-1]，K可以取值的范围是[0,N-2]。求这么多划分方案中，左部分中的最大值减去右部分最大值的绝对值，最大是多少？

给定整数数组A和数组的大小n，请返回题目所求的答案。

做法一：

思路：贪心算法

因为求的是两个最大值的差，所以肯定要找到数组中最大的那个值，然后就可以确定一边的最大值了。

另一边的最大值就是要找左右两端最小那个数，因为无论他们怎么往外扩都只能增大,不能减小。

无论怎么分组，两端的值是一定在两个组内的，如果两端的值小于最大值中间任一的值，那就只取这一个数字，因为要是的组内最大的值。

如果两端的值大于其中任一小的值，那这个组内的最大值，肯定不是这个小的值，所以无论如何右半边取最右端数字。

public int findMaxGap(int[] A, int n) {
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < A.length; i++) {
            if (max < A[i]){
                max = A[i];
            }
        }
        return max - Math.min(A[0],A[n - 1]);
    }

做法二：动态规划

dp[i][j]数组代表的是以i开始的，以j结尾的数组的最大值

public int findMaxGap(int[] A, int n) {
        int[][] dp = new int[n][n];
        for (int i = 0; i < n; i++) {
            dp[i][i] = A[i];
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                dp[i][j] = Math.max(dp[i][j-1],A[j]);
            }
        }
        int max = 0;
        for (int k = 0; k < n - 1; k++) {
            if (Math.abs(dp[0][k] - dp[k + 1][n - 1]) > max){
                max = Math.abs(dp[0][k] - dp[k + 1][n - 1]);
            }
        }
        return max;
    }

三、OR38 顺时针打印矩阵

顺时针打印矩阵_牛客题霸_牛客网 (nowcoder.com)

对于一个矩阵，请设计一个算法从左上角(mat[0][0])开始，顺时针打印矩阵元素。

给定int矩阵mat,以及它的维数nxm，请返回一个数组，数组中的元素为矩阵元素的顺时针输出。

思路：因为是要顺时针打印，所以规定顺序从右下左上右进行循环遍历

import java.util.*;

public class Printer {
    public int[] clockwisePrint(int[][] mat, int n, int m) {
        // write code here
        //左上角坐标
        int x1 = 0;
        int y1 = 0;
        //右下角坐标
        int x2= n-1;
        int y2= m-1;
        //定义数组
        int[] arr = new int[n*m];
        int index = 0;
        while(x1<=x2&&y1<=y2){
            //第一行:x1,yi~y2
            for(int i = y1;i <= y2;i++)
                arr[index++] = mat[x1][i];
            //最后一列：x1+1,x2,y2
            for(int i = x1+1;i <= x2;i++)
                arr[index++] = mat[i][y2];
            //最后一行：x2,,y2-1~y1;
            if( x1 < x2 ){
                for(int i= y2-1;i >= y1;i--)
                    arr[index++] = mat[x2][i];
            }
            //第一列:x2-1~x1+1,y1
            if(y1 < y2){
                for(int i = x2-1;i >= x1+1;i--)
                    arr[index++] = mat[i][y1];
            }
            x1++;
            y1++;
            x2--;
            y2--;
         
        }
         return arr;
    }
}

注意最后第一列的循环条件，是要i >= x1 + 1，因为上一次循环，包括了起始的值