【力扣周赛】第346场周赛
- 6439. 删除子串后的字符串最小长度
- 题目描述
- 解题思路
- 6454. 字典序最小回文串
- 题目描述
- 解题思路
- 6441. 求一个整数的惩罚数
- 题目描述
- 解题思路
6439. 删除子串后的字符串最小长度
题目描述
描述:给你一个仅由 大写 英文字符组成的字符串 s 。
你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 任一个 “AB” 或 “CD” 子字符串。
通过执行操作,删除所有 “AB” 和 “CD” 子串,返回可获得的最终字符串的 最小 可能长度。
注意,删除子串后,重新连接出的字符串可能会产生新的 “AB” 或 “CD” 子串。
输入:s = "ABFCACDB"
输出:2
解释:你可以执行下述操作:
- 从 "ABFCACDB" 中删除子串 "AB",得到 s = "FCACDB" 。
- 从 "FCACDB" 中删除子串 "CD",得到 s = "FCAB" 。
- 从 "FCAB" 中删除子串 "AB",得到 s = "FC" 。
最终字符串的长度为 2 。
可以证明 2 是可获得的最小长度。
输入:s = "ACBBD"
输出:5
解释:无法执行操作,字符串长度不变。
解题思路
难度:简单。
思路:最直观的想法是,令sub1="AB"作为子字符串1,令sub2="CD"作为子字符串2,当s字符串不为空时,在s中分别循环找到并删除sub1和sub2,当某一轮都没有找到时则退出循环,最后返回s的长度即可。
int minLength(string s)
{
string sub1="AB";
string sub2="CD";
while(s.size())
{
bool flag1=false,flag2=false;
while(s.find(sub1)!=string::npos)
{
s.erase(s.find(sub1),sub1.length());
flag1=true;
}
while(s.find(sub2)!=string::npos)
{
s.erase(s.find(sub2),sub2.length());
flag2=true;
}
if(!flag1&&!flag2)
break;
}
return s.size();
}
总结:在C++中可以使用字符串string对应的STL操作find来在一个字符串中查找另外一个字符串是否出现过以及出现的位置。s.find(sub),如果查找到,则返回其对应的位置,反之则返回string::npos;查找到具体位置后,则使用s.erase(s.find(sub),sub.length())来进行删除对应的子字符串即可。
6454. 字典序最小回文串
题目描述
描述:给你一个由 小写英文字母 组成的字符串 s ,你可以对其执行一些操作。在一步操作中,你可以用其他小写英文字母 替换 s 中的一个字符。
请你执行 尽可能少的操作 ,使 s 变成一个 回文串 。如果执行 最少 操作次数的方案不止一种,则只需选取 字典序最小 的方案。
对于两个长度相同的字符串 a 和 b ,在 a 和 b 出现不同的第一个位置,如果该位置上 a 中对应字母比 b 中对应字母在字母表中出现顺序更早,则认为 a 的字典序比 b 的字典序要小。
返回最终的回文字符串。
输入:s = "egcfe"
输出:"efcfe"
解释:将 "egcfe" 变成回文字符串的最小操作次数为 1 ,修改 1 次得到的字典序最小回文字符串是 "efcfe",只需将 'g' 改为 'f' 。
输入:s = "abcd"
输出:"abba"
解释:将 "abcd" 变成回文字符串的最小操作次数为 2 ,修改 2 次得到的字典序最小回文字符串是 "abba" 。
输入:s = "seven"
输出:"neven"
解释:将 "seven" 变成回文字符串的最小操作次数为 1 ,修改 1 次得到的字典序最小回文字符串是 "neven" 。
解题思路
难度:简单。
思路:最直观的想法是,双指针。使用i从前向后遍历,使用j从后向前遍历,如果s[i]小于s[j]则使s[j]等于s[i],反之如果s[i]大于s[j]则使s[i]等于s[j],最后返回s即可。
string makeSmallestPalindrome(string s) {
int len=s.size();
//双指针
for(int i=0,j=len-1;i<j;i++,j--)
{
if(s[i]>s[j])
s[i]=s[j];
else if(s[i]<s[j])
s[j]=s[i];
}
return s;
}
总结:只是在回文串的基础上加上了字典序最小的条件,其本质不变。
6441. 求一个整数的惩罚数
题目描述
描述:给你一个正整数 n ,请你返回 n 的 惩罚数 。
n 的 惩罚数 定义为所有满足以下条件 i 的数的平方和:
1 <= i <= n
i * i 的十进制表示的字符串可以分割成若干连续子字符串,且这些子字符串对应的整数值之和等于 i 。
输入:n = 10
输出:182
解释:总共有 3 个整数 i 满足要求:
- 1 ,因为 1 * 1 = 1
- 9 ,因为 9 * 9 = 81 ,且 81 可以分割成 8 + 1 。
- 10 ,因为 10 * 10 = 100 ,且 100 可以分割成 10 + 0 。
因此,10 的惩罚数为 1 + 81 + 100 = 182
输入:n = 37
输出:1478
解释:总共有 4 个整数 i 满足要求:
- 1 ,因为 1 * 1 = 1
- 9 ,因为 9 * 9 = 81 ,且 81 可以分割成 8 + 1 。
- 10 ,因为 10 * 10 = 100 ,且 100 可以分割成 10 + 0 。
- 36 ,因为 36 * 36 = 1296 ,且 1296 可以分割成 1 + 29 + 6 。
因此,37 的惩罚数为 1 + 81 + 100 + 1296 = 1478
解题思路
难度:中等。
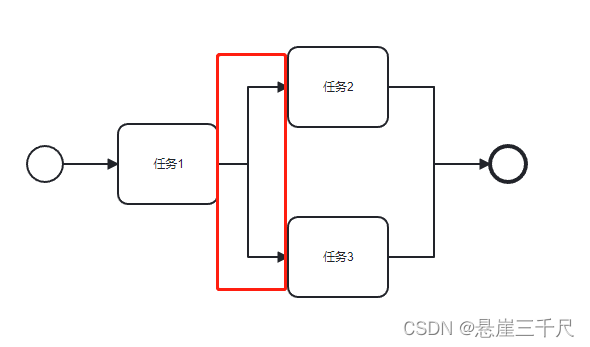
思路:最直观的想法是,回溯法。使用res记录结果,从1开始遍历到n,使用isS函数判断i的平方和i*i所分解得到的子字符串数值之和是否等于i,如果是则将i*i加入到res中,最后返回res即可。其中isS(i,ii)实现方法如下:首先将ii转换为字符串s,然后使用回溯法backtracking判断s从下标为0开始分割是否可以得到一组子字符串数值之和等于i,如果是则返回true,反之返回false。其中backtracking(s,0,i)实现方法如下:使用vector类型的int数组path存储s的子字符串分组,当到达叶子节点时,求解path中元素之和sum,如果sum等于i则返回true,反之返回false,每次进入回溯则遍历字符串,以下标作为界限,当前可遍历集合是从当前起始下标startIndex到字符串结尾的所有元素,先将[startIndex,i]转换为数值加入path,再使用回溯判断以i+1开始的字符串,如果返回值为true则表示可以找到一组,直接返回true即可,这样可以累加返回,反之没找到则做回溯处理,将元素从path中弹出,可结合回溯树理解。回溯树如下图所示:

vector<int> path;
bool backtracking(string &s,int startIndex,int target)
{
//终止条件 到达叶子结点
if(startIndex>=s.size())
{
int sum=0;
for(int i=0;i<path.size();i++)
sum+=path[i];
if(sum==target)
return true;
else
return false;
}
//遍历字符串 以下标作为界限
for(int i=startIndex;i<s.size();i++)
{
path.push_back(stoi(s.substr(startIndex, i - startIndex + 1)));
bool flag=backtracking(s,i+1,target);
if(flag)
return true;
path.pop_back();
}
return false;
}
//判断i*i是否有子串之和等于i
bool isS(int i,int ii)
{
//将数字转换为字符串方便判断
string s=to_string(ii);
path.clear();
if(backtracking(s,0,i))
return true;
return false;
}
int punishmentNumber(int n)
{
int res=0;
for(int i=1;i<=n;i++)
{
if(isS(i,i*i))
res+=i*i;
}
return res;
}
总结:遇到困难不要怕,先一步步分析应该如何去执行,然后分而治之分模块去逐步解决。