1. 算法效率对比
在此我们使用如下代码来测试各个算法的效率
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
CountSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("CountSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
}在这之中通过改变N的大小来改变需要被排序的数据量
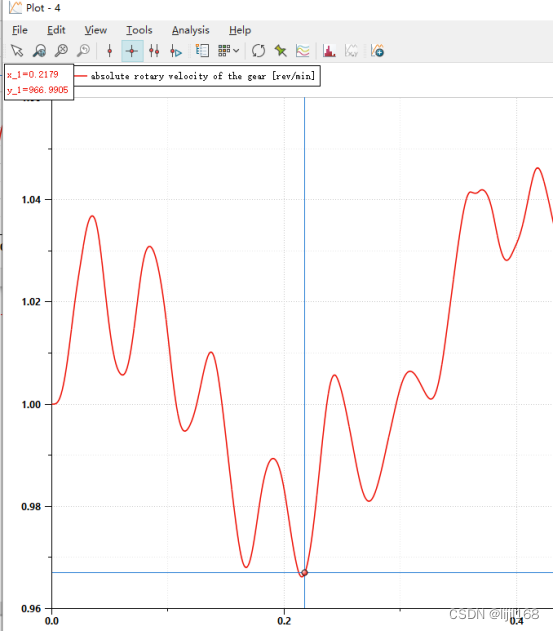
先对100000个数据排序有

我们发现此时插入排序与选择排序已经明显与其他排序不属于一个量级,接下来使用1000000个数据
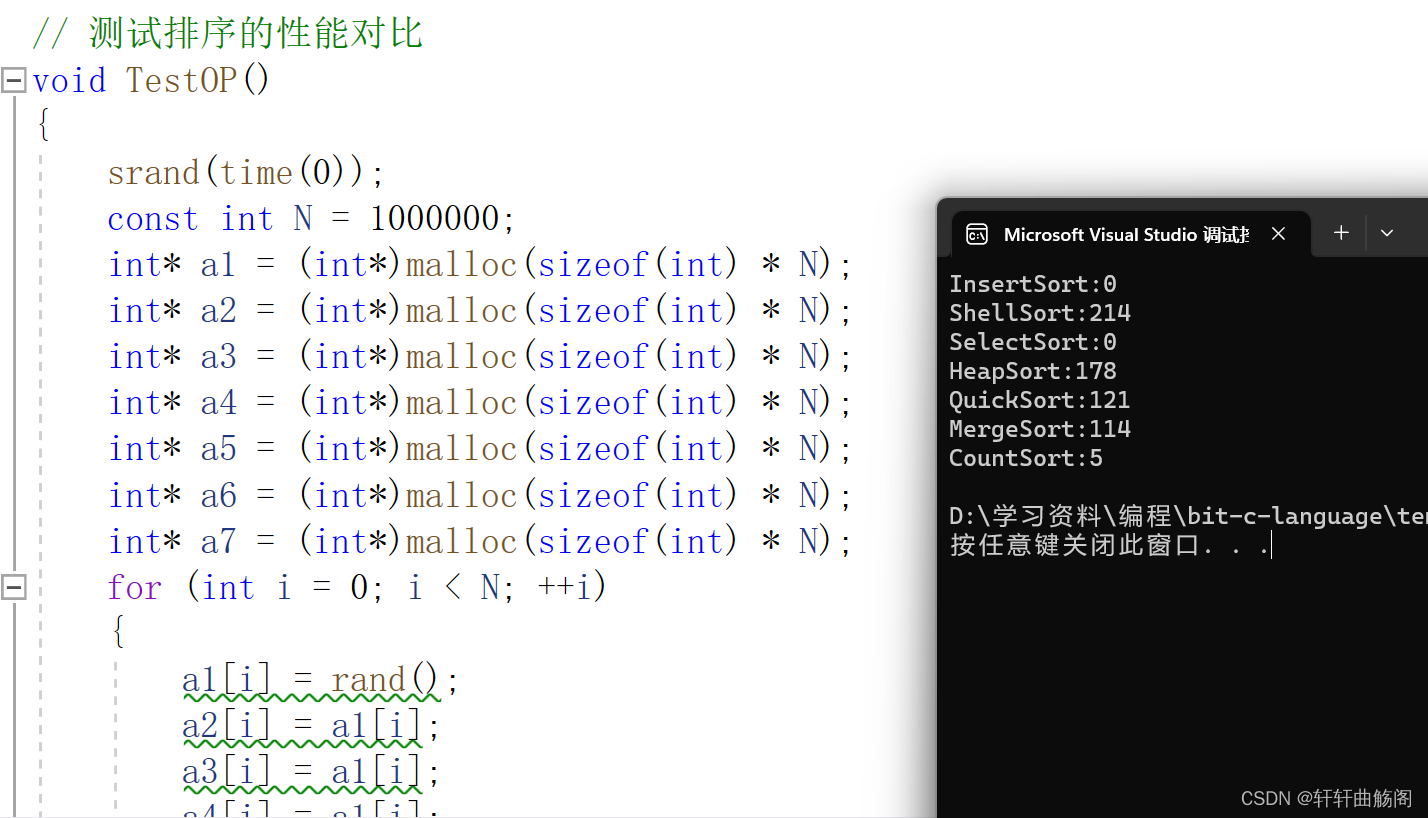
这之中我们发现计数排序效率较高是因为通过rand函数产生的数值区间的极差较小。
2. 总结
对于排序我们有如下的导图

且一谈到排序,我们都有下图
稳定性分析
冒泡排序:稳定
数据之间两两比较,当后面的数据较小时才被置换到前面,数据间的相对位置不改变,因此较为稳定
选择排序:不稳定
因为选择排序是确定一个最小(大)数后,将其放于最左(右)边,这就需要与最左(右)位置所在的数据作交换,从而造成数据相对位置改变,因此不稳定
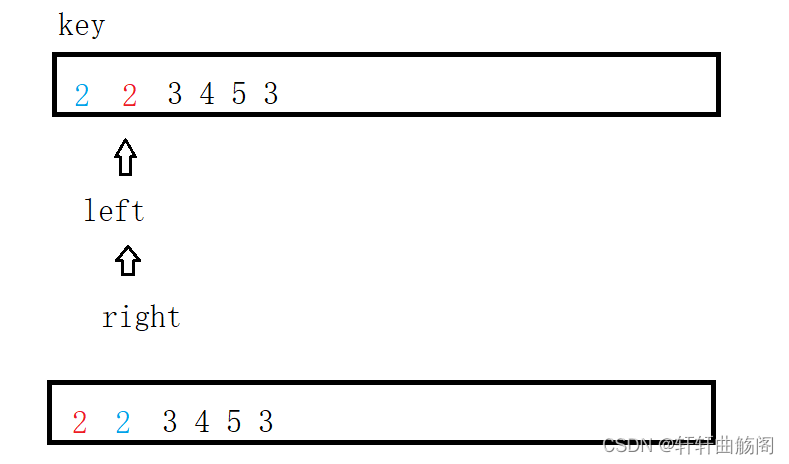
如
插入排序:稳定
插入排序是以当前位置为界向后寻找小于当前位置值的数,找到就将被找到的数插入到当前位置之前的位置,因此不会发生相对位置的改变,较为稳定
希尔排序:不稳定
希尔排序是以插入排序为基础,以gap分为不同组,而在分组过程中,相同的数据可能会被分到不同的组中,进而导致相对位置发生改变,因此不稳定
堆排序:不稳定
堆排序中,当交换堆顶元素和堆底元素时,可能会使原本在堆顶的相同元素移动到了堆底,而原本在堆底的相同元素移动到了堆顶,导致相同元素之间的相对顺序改变,因此不稳定
归并排序:稳定
归并排序中,只需要保证前数组中的较小或相等值先存放在临时数组中,就可以做到不影响元素间的相对位置,从而做到稳定
快速排序:不稳定
在快速排序中,当遍历数组中的元素进行分区操作时,可能会交换相同值的元素的位置,从而导致相同值的元素的相对顺序发生改变。
如