作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:Java初阶数据结构
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!
文章目录
前言
一、选择排序
1.1 算法思路
1.2 代码实现
1.3 特性总结
二、堆排序(从小到大)
2.1 算法思路
2.2 代码实现
2.3 特性总结
总结

前言
今天我们将介绍另外的两种常见的算法,即选择排序算法和堆算法;这两个算法也是非常重要的算法,必须要好好掌握才行;
一、选择排序
1.1 算法思路
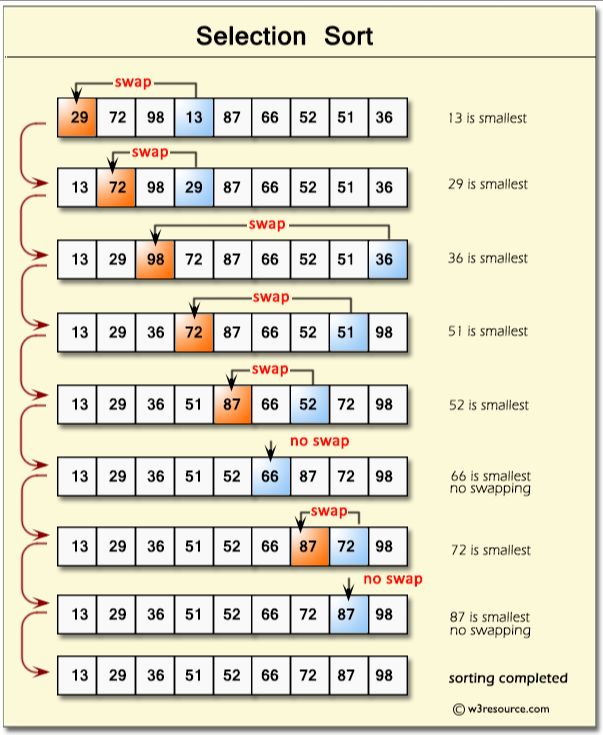
动画图示:
算法思路:
在遍历数组的过程中,从当前遍历的数组元素的下一个元素开始,向后找出剩余数组元素中的最小值,让这个最小值和当前遍历到的数组元素进行交换;
详细说就是:
- 在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
1.2 代码实现
/** * 选择排序 * @param array */ public static void selectSort(int[] array) { for (int i = 0; i < array.length; i++) { int minIndex = i; for (int j = i + 1; j < array.length; j++) { if (array[j] < array[minIndex]) { // 注意这里不能是array[i] < array[j]因为j在这个循环里是静态的,我们排序要求是动态的 minIndex = j; // 比如[1、34、56、12、23], i下标所对应的数组的值一开始等于34,j -> 12是满足条件,minIndex更新,等于12所对应的下标 // 但如果是array[i] < array[j],此时array[j]还等于34,等于遇到23,条件仍然满足,minIndex又更新了,但其实这个时候不应该更新,因为刚才的12就是从i下标往后的数组中最小的值了 } } int tmp = array[i]; array[i] = array[minIndex]; // 如果每找到,minIndex = i,相当于是自己和自己进行交换 array[minIndex] = tmp; } }
1.3 特性总结
- 1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 2. 时间复杂度:O(N^2)
- 3. 空间复杂度:O(1)
- 4. 稳定性:不稳定
选择排序为啥不是稳定性排序呢????举个例子:数组 6、7、6、2、8,在对其进行第一遍循环的时候,会将第一个位置的6与后面的2进行交换。此时,就已经将两个6的相对前后位置改变了。因此选择排序不是稳定的排序算法;
二、堆排序(从小到大)
2.1 算法思路
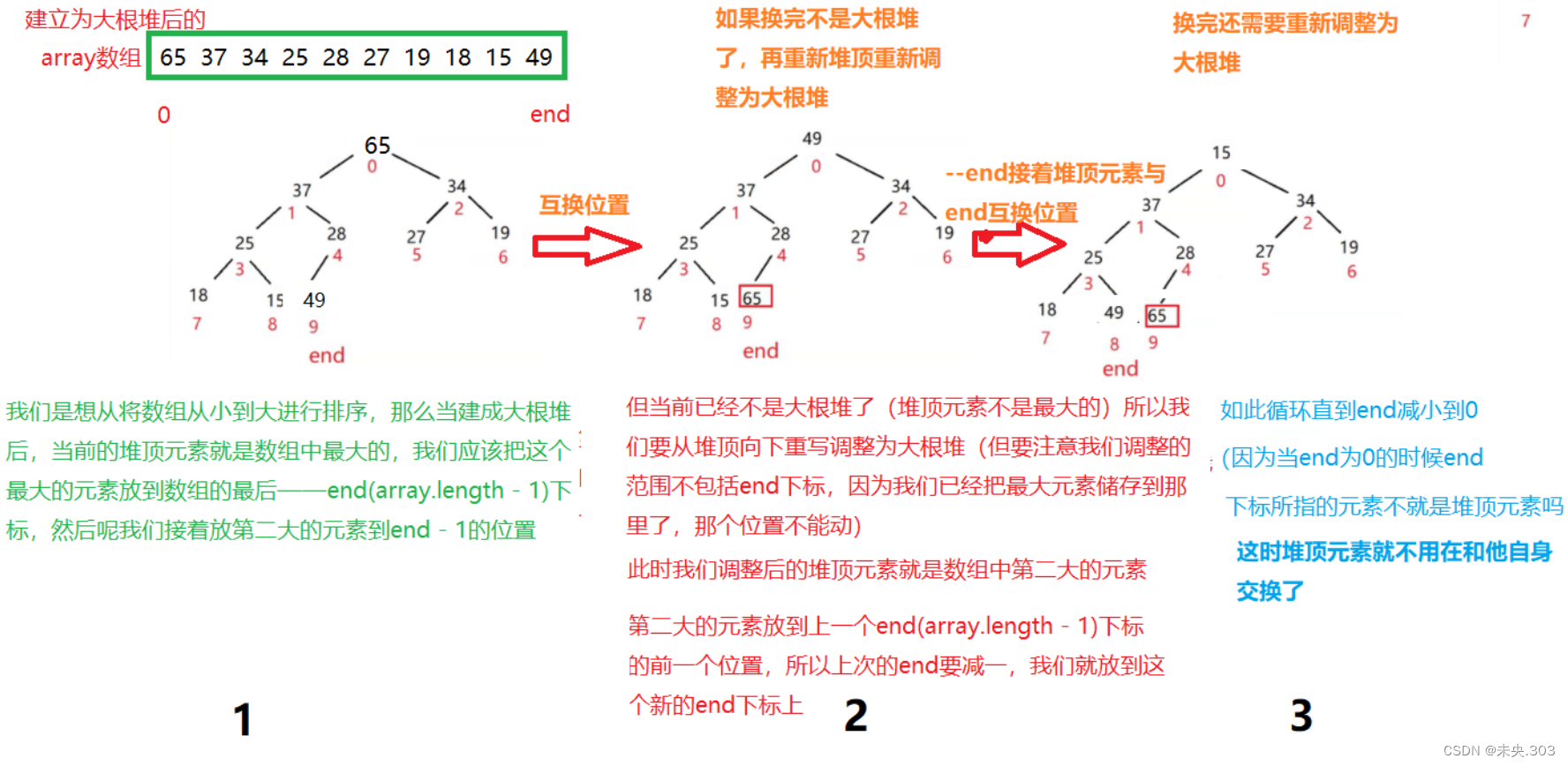
- 将要排序的数组建立为大根堆
- 堆顶元素(当前数组的最大值)与数组end下标的元素互换位置
- 然后从堆顶向下调整为大根堆,这里要注意调整时的边界条件end是在不断变化的,当前end也不断在变化着的,每调整一次end就减一,直到end == 0
图示分析:
2.2 代码实现
import java.util.Arrays;
// 堆排序完整代码测试
public class heapSortTest {
// 向下调整为大根堆
public static void shiftDownBig(int[] array, int root, int len) {
int parent = root;
int child = 2 * parent + 1;
while (child < len) {
if (child + 1 < len && array[child] < array[child + 1]) {
child = child + 1;
}
if (array[child] > array[parent]) {
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
parent = child;
child = 2 * parent + 1;
}
else {
break;
}
}
}
// 大根堆的创建(这里我们用到是向下调整建立大根堆,时间复杂度O(n)——如果是向上调整建立大根堆堆,时间复杂度是O(n * log2N)
public static void createHeap(int[] array) {
for (int i = (array.length - 1 - 1) / 2; i >= 0; --i) {
shiftDownBig(array, i, array.length);
}
}
/**
* 堆排序,从小到大排序——建立大根堆(原地排序,在数组本身排序)
* @param
*/
public static void heapSort(int[] array) {
// 1、先建立一个大根堆,建堆的时间复杂度为O(n)因为我们是通过向下调整来建堆的
createHeap(array);
// 2、将当前堆顶元素(array[0])与堆中end下标的元素互换位置,然后向下调整,保证仍为大根堆——这样堆顶元素仍旧是当前数组中最大的元素
// end从堆中最后一个元素开始,保证堆中(数组)的最大值在堆中最后一个元素的位置,然后倒数第二大、第三大元素接着从array.length - 2开始向前排
for (int end = array.length - 1; end > 0; --end) {
int tmp = array[end];
array[end] = array[0];
array[0] = tmp;
// 调整0下标这棵树仍为大根堆
shiftDownBig(array, 0, end);
// 保证调整完后是大根堆,注意这里的结束位置是end,end后面是用到存放数组前k个元素的,如果结束位置是array.length,那么我们之前放到数组array.length - 1下标的数组最大值就又被调整了
}
// 具体堆排的时间复杂度为 O(n * logn)--总的时间复杂度就是(n + n * logn)即O(n * log以2为底的n)
}
public static void main(String[] args) {
int[] array = {23, 42, 13, 12, 28};
heapSort(array);
System.out.println(Arrays.toString(array));
}
}运行结果:
2.3 特性总结
1、堆排序使用堆来选数,效率就高了很多。
2、时间复杂度:O(N*logN)
3、空间复杂度:O(1)
4、稳定性:不稳定;
总结
今天的两种算法就介绍到这里了,一定要熟练掌握这两种算法使用;