位运算符详解
前言:由于位运算符是直接对二进制数操作,因此对二进制、八进制、十六进制不甚了解的小伙伴建议先看这篇二进制、八进制、十六进制与十进制的相互关系,这样阅读本篇时将事半功倍
总览
位运算是对计算机存储的二进制序列的相应位进行操作
位运算的操作数必须是整数型或字符型
运算符 示例 按位与 & a & b 按位或 | a | b 按位异或 ^ a ^ b 按位取反 ~ ~ a 左移 << a << b 右移 >> a >> b
按位与 &
按位与是指:参加运算的两个操作数,按二进制对应的位进行“与”运算。如果两个相应的二进制位都为1,则得到的结果为1,否则位0。
0 & 0 = 0,0 & 1 = 0,1 & 1 = 1,1 & 0 = 0,即 全一为1,有零则零
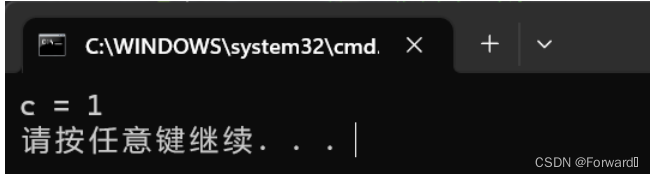
int a = 15; //15的二进制序列为 0000 0000 0000 0000 0000 0000 0000 1111 int b = 17; //16的二进制序列为 0000 0000 0000 0000 0000 0000 0001 0001 int c = a & b; //a和b按位与,那么得到的二进制序列应该是 0000 0000 0000 0000 0000 0000 0000 0001 //即十进制的1 printf("c = %d\n", c);
按位或 |
两个相应的二进制位中只要有一个为1,则得到的结果为1。
0 | 0 = 0,0 | 1 = 1,1 | 0 = 1,1 | 1 = 1,即 有一为1,全零为0
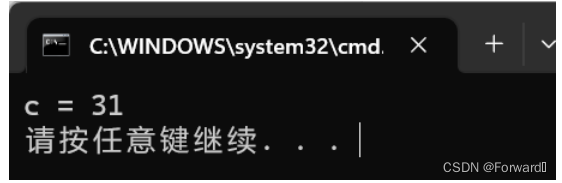
int a = 15; //15的二进制序列为 0000 0000 0000 0000 0000 0000 0000 1111 int b = 17; //16的二进制序列为 0000 0000 0000 0000 0000 0000 0001 0001 int c = a | b; //a和b按位与,那么得到的二进制序列应该是 0000 0000 0000 0000 0000 0000 0001 1111 //即十进制的31 printf("c = %d\n", c);
按位异或 ^
参加运算的两个二进制位,如果相同则为0,不同则为1
1 ^ 1 = 0,1 ^ 0 = 1,0 ^ 1 = 1,0 ^ 0 = 0,即 不同为1,相同为0
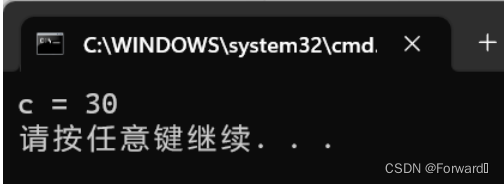
int a = 15; //15的二进制序列为 0000 0000 0000 0000 0000 0000 0000 1111 int b = 17; //16的二进制序列为 0000 0000 0000 0000 0000 0000 0001 0001 int c = a ^ b; //a和b按位与,那么得到的二进制序列应该是 0000 0000 0000 0000 0000 0000 0001 1110 //即十进制的30 printf("c = %d\n", c);
按位取反 ~
将二进制中的每个位的 0变成1,1变成0
如 ~025就是对八进制数25(即二进制数000 010 101)进行按位取反,得到752(111 101 010)
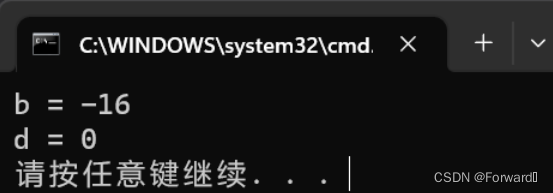
int a = 15; //15的二进制序列为 0000 0000 0000 0000 0000 0000 0000 1111 int b = ~ a; //a按位取反,二进制序列为 1111 1111 1111 1111 1111 1111 1111 0000 // 由于在计算机内部是按补码储存,那么转换为反码 1111 1111 1111 1111 1111 1111 1110 1111 // 转化为原码 1000 0000 0000 0000 0000 0000 0001 0000 //即十进制的-16 printf("b = %d\n", b); int c = -1; //-1的二进制序列为 1111 1111 1111 1111 1111 1111 1111 1111 int d = ~c; //c按位取反,二进制序列为 0000 0000 0000 0000 0000 0000 0000 0000 //即十进制的0 printf("d = %d\n", d);
左移 <<
左移运算符是用来将一个数的各二进制位全部向左移动若干位,右边的空位补零
例如 a = 3(10) = 011(2),那么 a << 1的结果就是110(2)=6(10)
int a = 17; //a的二进制序列为 0000 0000 0000 0000 0000 0000 0001 0001 int b = a << 2; //b为所有二进制为左移两位得到 0000 0000 0000 0000 0000 0000 0100 0100 //即十进制数 68 printf("b = %d\n", b);
右移 >>
- 右移运算符是用来将一个数的各二进制位全部向右移动若干位
- 逻辑右移:右移之后的空位无论原符号位是什么,统一补零
- 算术右移:如果原符号位位1,那么空位全部补1,反之如果符号位为0,那么空位补0
- 一般来说,编译器采用的是算术右移
int a = 17; //a的二进制序列为 0000 0000 0000 0000 0000 0000 0001 0001 int b = a >> 2; //b为所有二进制为左移两位得到 0000 0000 0000 0000 0000 0000 0000 0100 //即十进制数4 int c = -15; //c的二进制原码序列为 1000 0000 0000 0000 0000 0000 0000 1111 //反码 1111 1111 1111 1111 1111 1111 1111 0000 //补码 1111 1111 1111 1111 1111 1111 1111 0001 int d = c >> 2; //如果是逻辑右移 //d的二进制序列为 0011 1111 1111 1111 11111 1111 1111 1100 //如果是算术右移 //d的二进制序列为 1111 1111 1111 1111 1111 1111 1111 1100 //反码 1111 1111 1111 1111 1111 1111 1111 1011 //原码 1000 0000 0000 0000 0000 0000 0000 0100 //即十进制数-4 printf("b = %d\n", b); printf("d = %d\n", d);
位运算的运用
判断一个数是否为偶数
Tips:利用位运算对一个数进行奇偶判断的速度要快于if(num % 2 == 0){……}这一操作
我们知道二进制数每一位的权重为2,因此要判断一个数是否为偶数,只需要判断它二进制位的第一位是1还是0
- 如果第一位是1,那么十进制值就会加上20 = 1这个奇数,而偶数加奇数一定为奇数,因此该数一定是奇数
- 如果第一位是0,那么这个1就不会加上,该数就一定是偶数
那我们如何得到二进制数的第一位呢?将这个数和1进行按位与操作就可以了,因为1的二进制位只有第一位为1,这样我们就可以单独对二进制的第一位进行判断,从而判断该数的奇偶性
#include<stdio.h> int main() { int a; while (scanf_s("%d", &a) != EOF) { //注意:关系运算符的优先级高于&,|,^操作符 if ((a & 1) == 0) printf("%d是偶数\n",a); else printf("%d是奇数\n", a); } return 0; }
统计二进制数中1的个数
方法一
我们知道如果我们要获得十进制数的每一位,我们可以对这个数不断进行模10除以10操作
- 例如要获得十进制数139的每一位,139 % 10 = 9,得到各位9,139 / 10 = 13,13 % 10 = 3,得到十位3,13 / 10 = 1,1 % 10 = 1,得到百位1
那么对二进制数也可以这样操作,只是将模10除以10改为模2除以2
int One_Count(unsigned int num) //参数定义为无符号型是为了确保对负数运算的正确 { int count = 0; while (num) { if (num % 2 == 1) count++; num /= 2; } return count; }
方法二
可以利用 & 获得二进制的每一位
int One_Count(int num) { int count = 0; for (int i = 0; i < 32; i++) { if (((num >> i) & 1) == 1) count++; } return count; }
方法三(巧解)
可能有小伙伴会认为上面的方法二中的循环固定要循环32次,当计算小数字二进制中1的个数时会浪费时间,那么还有没有更加极致的方法呢?
有!我们来看一个表达式:n = n & (n - 1)
举个例子,n = 15(10) = 1111(2), n - 1 = 14(10) = 1110(2), n = n & (n-1) = 1110(2)
n = 1110(2), n - 1 = 1101(2), n = n & (n-1) = 1100(2)
n = 1100(2), n - 1 = 1011(2), n = n & (n-1) = 1000(2)
n = 1000(2), n - 1 = 0111(2), n = n & (n-1) = 0000(2)
我们可以发现,这个表达式每一次计算,都可以将数n二进制位中最右边的1变成0,因此我们可以创建一个循环,n = n & (n - 1)这个表达式可以运行的次数就是数n二进制位中含1的个数
int One_Count(int num) { int count = 0; while (num) { num = num & (num - 1); count++; } return count; }
统计两个二进制数中不同位的个数
根据按位异或 ^ 的规律,两个二进制位如果不同,则结果为1,相同结果为0,因此我们可以将这两个数先按位异或,在统计结果二进制位中1的个数
#include<stdio.h> int One_Count(int num) { int count = 0; while (num) { num = num & (num - 1); count++; } return count; } int main() { int a, b, c; scanf_s("%d %d", &a, &b); c = a ^ b; printf("%d和%d二进制不同位有%d个\n", a,b,One_Count(c)); return 0; }
将一个数用二进制形式打印(左边为高位,右边为地位)
#include<stdio.h> void Print(int num) { unsigned int temp = 0x80000000; //即二进制数 1000 0000 0000 0000 0000 0000 0000 0000 //第一位不看成符号位 while (temp) { if ((num & temp)) printf("1 "); else printf("0 "); temp >>= 1; } } int main() { int a; scanf_s("%d", &a); Print(a); printf("\n"); return 0; }
不创建临时变量交换两个数
这里我们要用到按位异或 ^
这种方法的运行效率不如创建临时变量
void exchange(int *a, int *b) { int temp = *a; *a = *b; *b = temp; }这种方法仅作了解即可
#include<stdio.h> int main() { int a = 2, b = 3; a = a ^ b; b = a ^ b; a = a ^ b; return 0; }