| 三、实验原理及内容 实验原理: 1、用贪心法实现求两序列的一般背包问题。要求掌握贪心法思想在实际中的应用,分析一般背包的问题特征,选择算法策略并设计具体算法,编程实现贪心选择策略的比较,并输出最优解和最优解值。 2、用贪心法求解带时限的(单位时间)作业排序问题,求得最优的计算次序以使得作业按 序完成,并收益最大 实验内容:
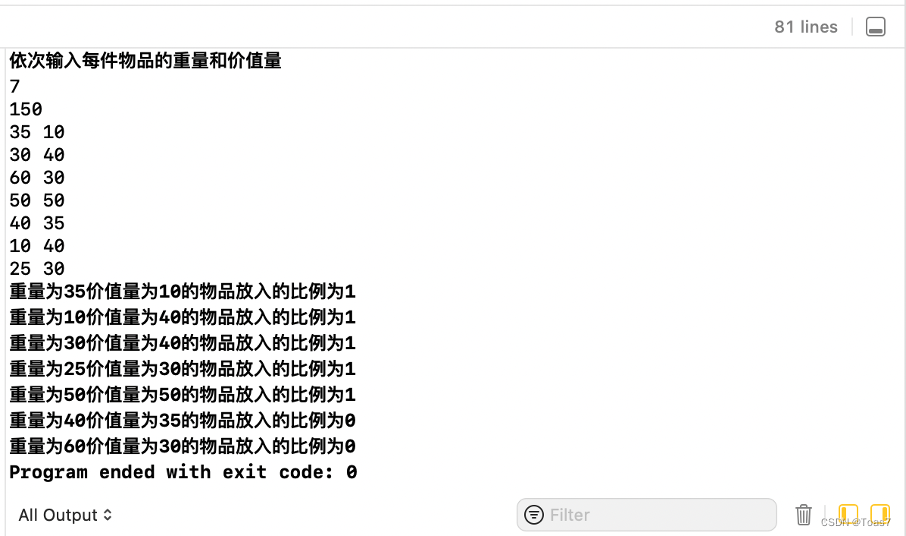
标准 1:选取目标函数(总价值)作为量度标准,每次取价值最大的物品装包,不考虑重量. 标准 2:选取重量作为量度标准,每次取重量最小的物体装包,不考虑收益. 标准 3:选取单位重量价值最大的物品装包,即每次选 pi/wi 最大的物品装包.标准最合理, 得到最优解.(正确性有待证明) 基本步骤: 1、首先计算每种物品单位重量的价值 Pi/Wi 并按非增次序进行排序; 2、然后依贪心选择策略,选择单位重量价值最高的物品装入背包。依此策略一直地进行下去,将尽可能多的物品全部装入背包,直到将背包装满。 3、若装入某件物品时,不能全部装下,而背包内的物品总重量仍未达到 W,则根据背包的剩余载重,选择单位重量价值次高的物品并尽可能多地装入背包。 代码实现: 实验结果: 由实验结果可得知背包成功
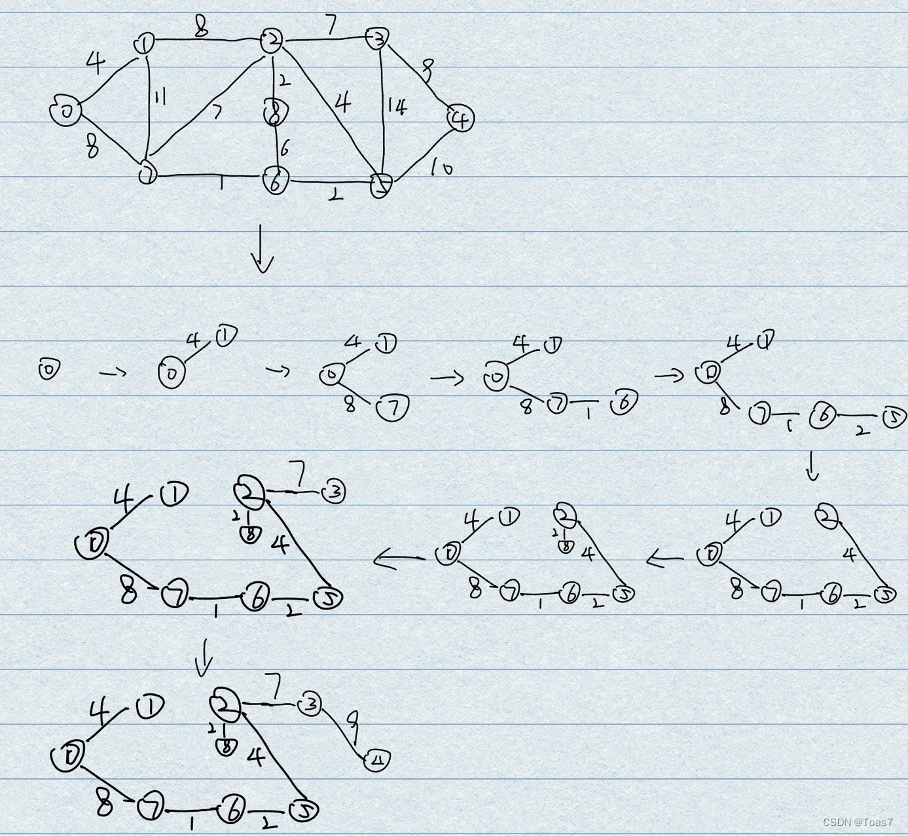
设 G=(V,E)是一个连通带权图,V={1,2,…,n}。构造 G 的一棵最小生成树 F=(U,S)的 Prim 算法的基本步骤是: (U 为正在构造的生成树点集) 1、首先从图的任一顶点起进行,将它加入集合 U 中。如:置 U={1}; 2、然后作如下的贪心选择:每次从与集合 U 相关联的边中(即一个端点在集合中而另一个端点在集合外的各条边中),选出权值 c[i][j]最小的一条作为生成树的一条边,此时满足条件 iU,jV-U,并将集合外的结点 j 加入集合中,表示该点也被所选出的边连通了。 3、这个过程一直进行到 U=V 时为止,这时全部顶点都加入到集合 U 中。在这个过程中选取到的所有边恰好构成 G 的一棵最小生成树。
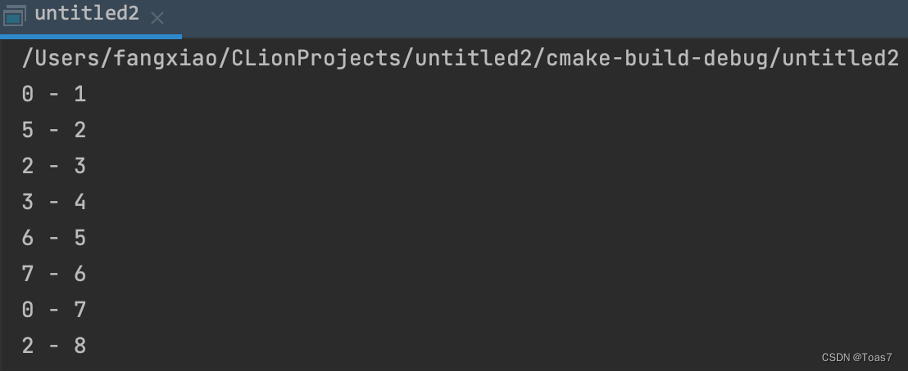
实验结果:
测试数据与实验结果:
实验结果与预设结果一致。
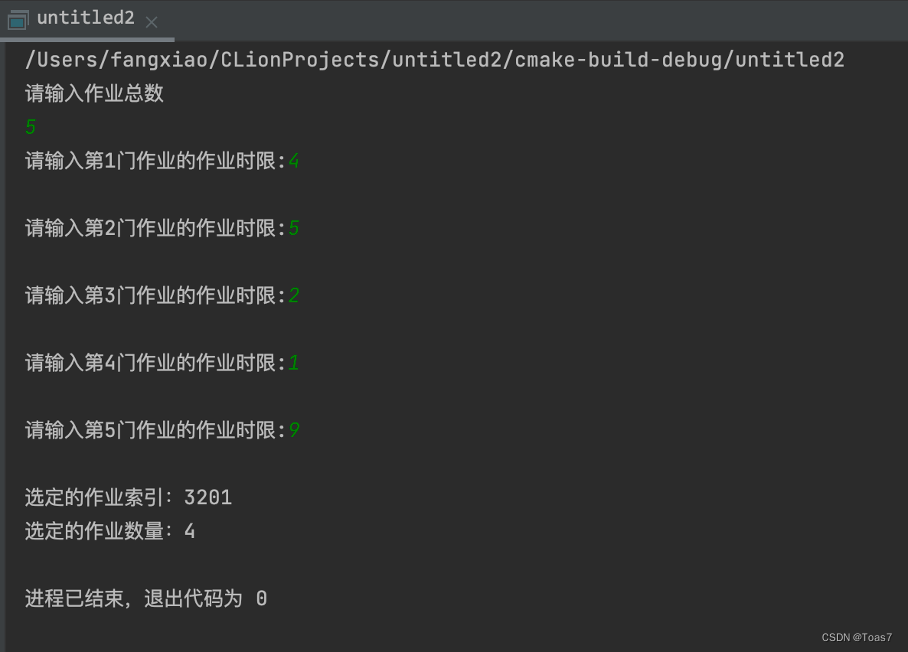
有n 个作业,每个作业都有一个截止期限di>0(di 为整数)。每个作业运行时间为1 个单 位时间。每个作业若能够在截止期限内完成,可获得pi>0 的收益。 要求: 得到一种作业调度方案,给出作业的一个子集和该子集的一种排列,使子集中的作业都能 如期完成,并且获得最大的收益。 代码实现: 实验结果:
由实验结果可得知我们创建了一个时限作业数组d[]=[4,5,2,1,9];经过算法排序后得出结果:3201,且选定的作业数量为4 |
南京邮电大学算法与设计实验二:贪心算法(最全最新,与题目要求一致)
news2026/2/7 11:51:34
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/547641.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
图的遍历,最小生成树,最短路径算法的手算。
1.图的遍历
按照某种规则沿着图中的边对图中的所有顶点访问一次且仅访问一次。 注:图是一种特殊的树。
1.广度优先遍历BFS
不难看出,图的广度优先就是参照的树的层次遍历算法。
2.深度优先遍历
从某个顶点开始V,访问这个顶点V相邻的任意…
【音视频开发】视频编码格式:YUV
文章目录 分类标准分类 简介 参考:YCbCr与YUV
分类标准 首先,我们可以将 YUV 格式按照数据大小分为三个格式,YUV 420,YUV 422,YUV 444。由于人眼对 Y 的敏感度远超于对 U 和 V 的敏感,所以有时候可以多个 …
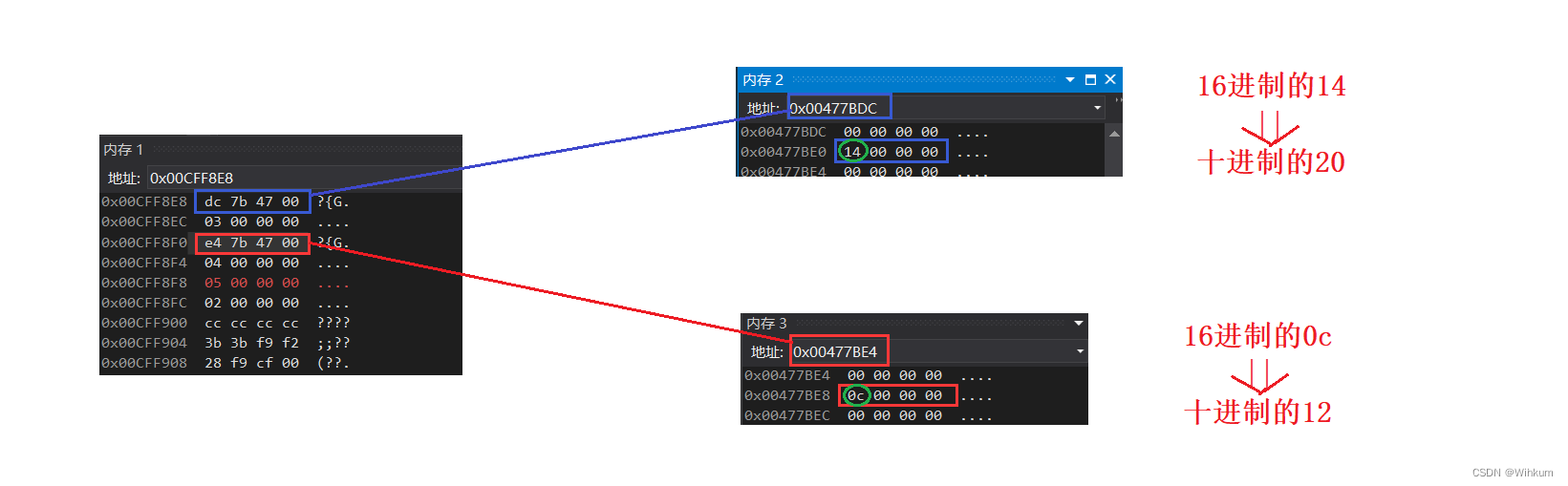
位运算符及其相关操作详解
位运算符详解 前言:由于位运算符是直接对二进制数操作,因此对二进制、八进制、十六进制不甚了解的小伙伴建议先看这篇二进制、八进制、十六进制与十进制的相互关系,这样阅读本篇时将事半功倍 总览 位运算是对计算机存储的二进制序列的相应位进…
【笔试强训选择题】Day17.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 前言
目…
南京邮电大学算法与设计实验三:动态规划法(最全最新,与题目要求一致)
实验原理:
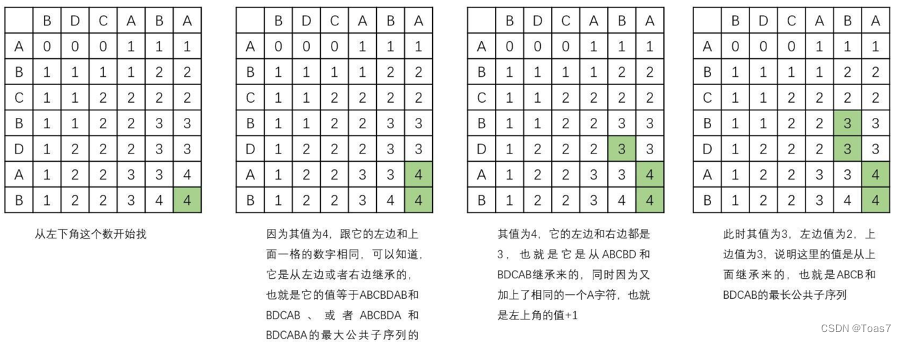
1、用动态规划法和备忘录方法实现求两序列的最长公共子序列问题。要求掌握动态规划法思想在实际中的应用,分析最长公共子序列的问题特征,选择算法策略并设计具体算法,编程实现两输入序列的比较,并输出它们的…
Linux之NetLink学习笔记
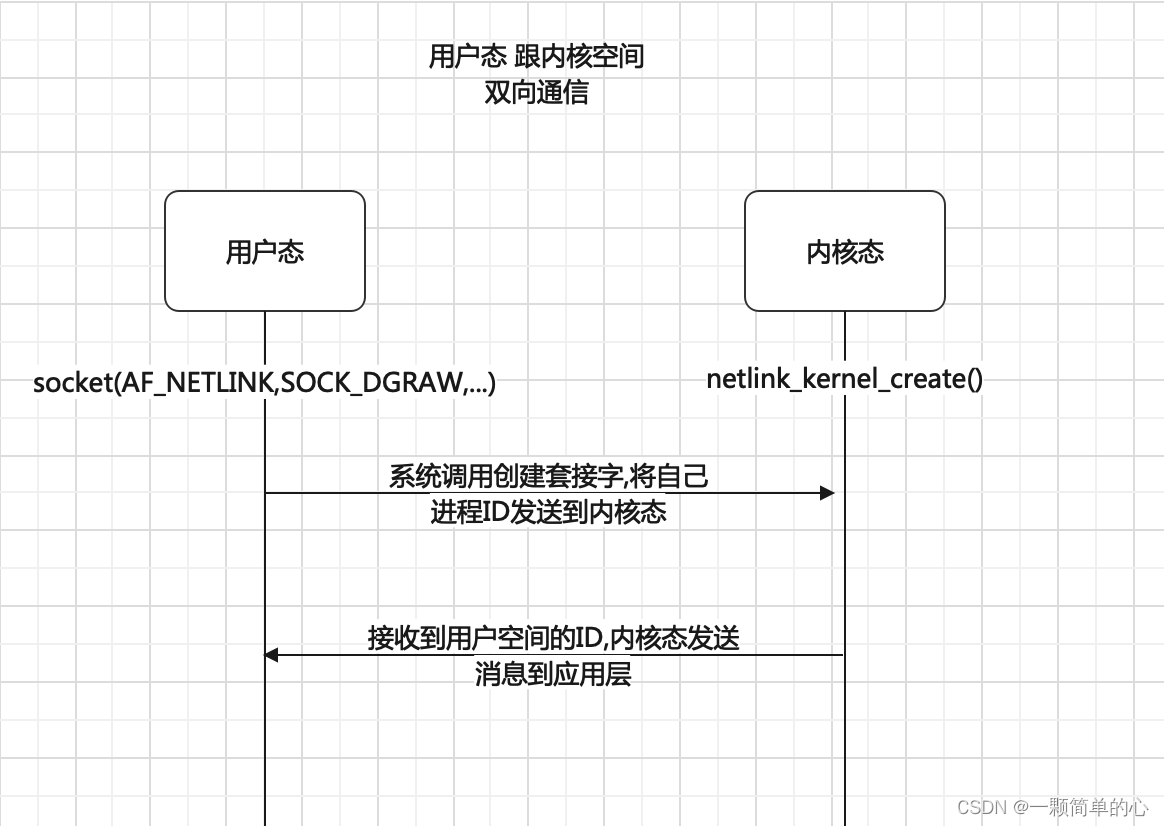
1.NetLink机制
NetLink是一种基于应用层跟内核态的通信机制,其特点是一种异步全双工的通信方式,支持内核态主动发起通信的机制。该机制提供了一组特殊的API接口,用户态则通过socket API调用。内核发送的数据再应用层接收后会保存在接收进程socket的缓存…
MediaPipe虹膜检测:实时虹膜跟踪和深度估计
包括计算摄影(例如,人像模式和闪光反射)和增强现实效果(例如,虚拟化身)在内的大量实际应用都依赖于通过跟踪虹膜来估计眼睛位置。一旦获得了准确的光圈跟踪,我们就可以确定从相机到用户的公制距离,而无需使用专用的深度传感器。反过来,这可以改善各种用例,从计算摄影…
《Kali渗透基础》01. 介绍
kali渗透 1:渗透测试1.1:安全问题的根源1.2:安全目标1.3:渗透测试1.4:标准 2:Kali2.1:介绍2.2:策略2.3:安装 3:Kali 初步设置3.1:远程连接3.1.1&a…
深度学习之全过程搭建卷积神经网络(CNN)
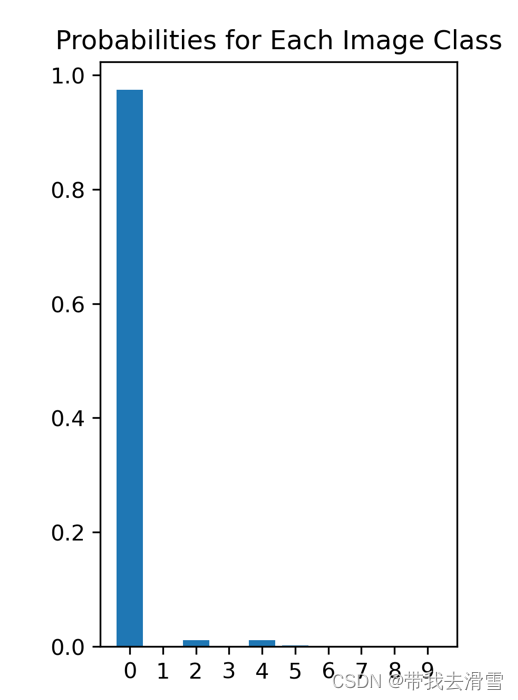
大家好,我是带我去滑雪! 本期将尝试使用CIFAR-10 数据集搭建卷积神经网络,该数据集由 10 个类别的 60000 张 32x32 彩色图像组成,每个类别有 6000 张图像。 下面开始全过程搭建CNN识别彩色图片:
目录 (1&a…
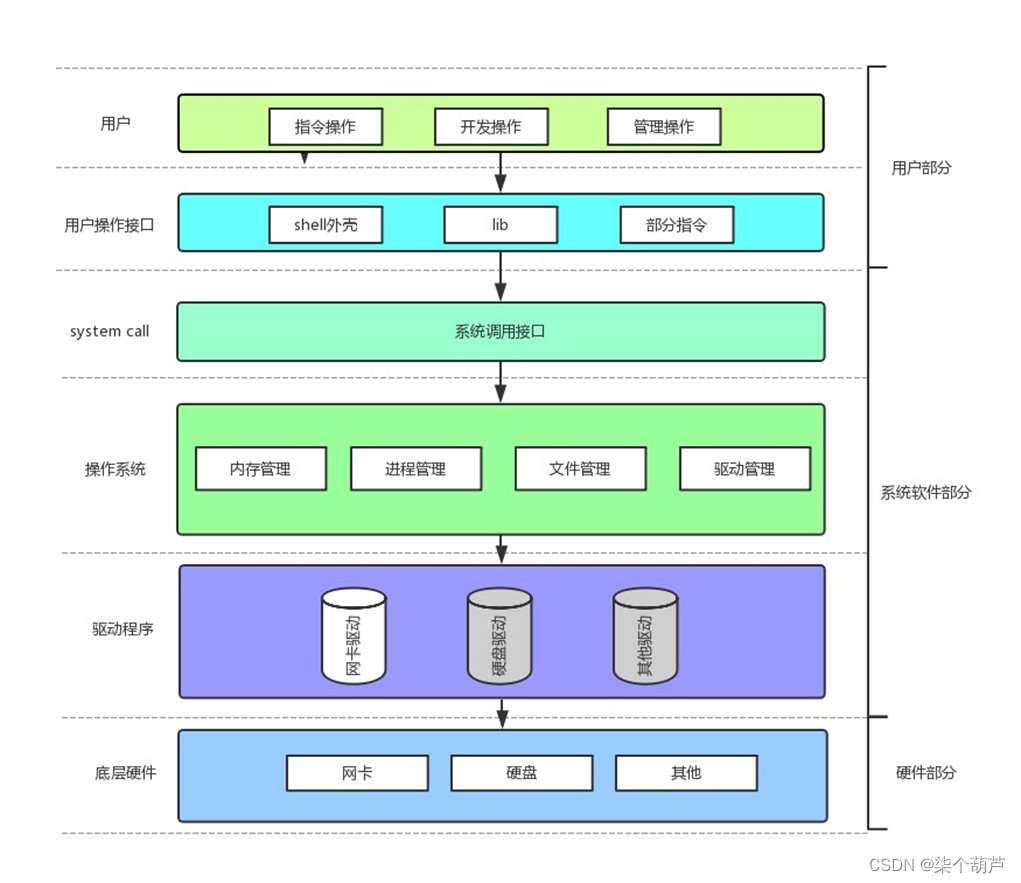
【Linux】冯诺依曼与操作系统
目录 一、冯诺依曼结构体系1、冯诺依曼结构体系简介2、为什么要有内存呢? 二、操作系统1、操作系统如何对硬件进行管理?2、操作系统为什么要对软硬件进行管理? 一、冯诺依曼结构体系
1、冯诺依曼结构体系简介
在现实生活中,我们…
KEYSIGHT MSOS204A 2GHZ 4通道DSOS204A高清晰度示波器
KEYSIGHT是德DSOS204A/MSOS204A高清晰度示波器
附加功能: 2 GHz 带宽(可升级) 4 个模拟通道和 16 个数字通道 最大存储深度:800 Mpts(2 通道),400 Mpts(4 通道) 最大…
菱形继承、菱形虚拟继承、以及菱形虚拟继承的模型结构内部。
1. 单继承:一个子类只有一个直接父类。 多继承:一个子类有两个或以上直接父类。 菱形继承:菱形继承是多继承的一种特殊情况。 下面是代码和对象模型结构,可以看出菱形结构存在哪些问题,如下:
#define _CR…
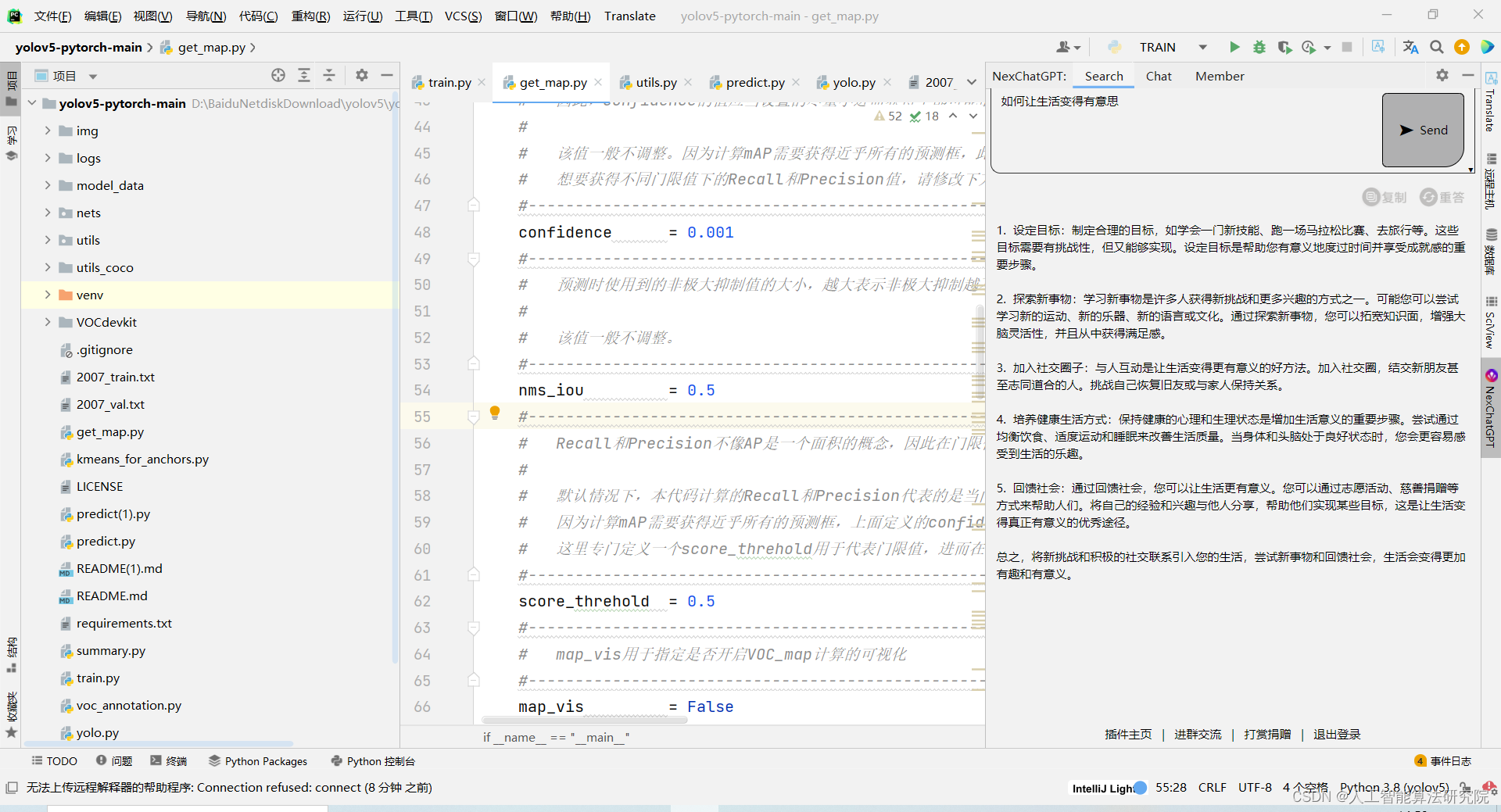
学习经验分享【30】Pycharm插件chatgpt,用来辅助编写代码
在Pycharm中发现ChatGPT插件,很好用,免费安全,大家可以作为编代码的辅助工作,也可用来玩GPT的接口。具体方法如下 实现效果如下: 更多精彩内容敬请持续关注。如果本博文对你有帮助的话,欢迎点赞、评论区留言…
BUUCTF-一叶障目 解析
打开文件发现一张png图片,里面没有内容,使用tweakpng打开 tweakpng报错 ,说明crc校验值对不上
有两种可能,一是crc值被修改,二是图片的宽高被修改(在ctf中多半是后者)
先尝试修改crc值为55900…
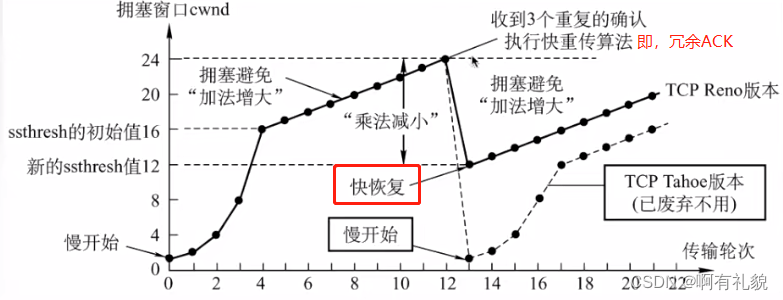
【王道·计算机网络】第五章 传输层
一、传输层概述
传输层为应用层提供通信服务,使用网络层服务传输层的功能: 提供进程和进程之间的逻辑通信(网络层提供主机之间的逻辑通信)复用(发送发不同的应用进程)和分用(接收方正确的数据传…
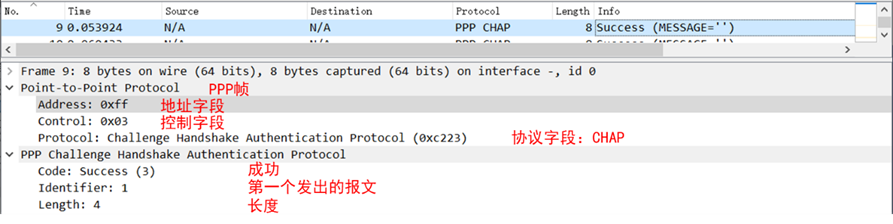
【网络协议详解】——PPP协议(学习笔记)
目录 🕒 1. 数据链路层协议概述🕒 2. PPP协议分析🕘 2.1 概述🕘 2.2 工作流程🕘 2.3 帧格式 🕒 3. LCP协议🕘 3.1 概述🕘 3.2 报文格式🕘 3.3 报文种类🕤 3.3…
3年经验,面试测试岗只会功能测试开口要求18K,令我陷入沉思
由于朋友临时有事, 所以今天我代替朋友进行一次面试,公司需要招聘一位自动化测试工程师,我以很认真负责的态度完成这个过程, 大概近30分钟。 主要是技术面试, 在近30分钟内, 我与被面试者是以交流学习的方式…
STM32F407+LWIP+DP83848以太网驱动移植
最近有个项目上需要用到网络功能,于是开始移植网络相关代码。在移植的过程中感觉好难,网上找各种资料都没有和自己项目符合的,移植废了废了好的大劲。不过现在回头看看,其实移植很简单,主要是当时刚开始接触网络&#…
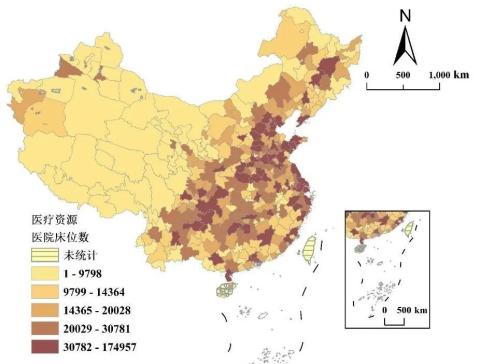
【数据分享】2020年我国地级市医疗资源空间分布数据(Shp格式/Excel格式)
医疗资源的配置情况直接反映了一个城市的发展水平,医疗资源相关数据也是经常使用到的数据!
我们发现学者刘海猛在科学数据银行(ScienceDB)平台上分享了2020年我国341个城市(地区、州、盟)的基础医疗资源数…
电脑安装软件时,如何避免捆绑安装?
在网络上非正规网站下载安装软件时,经常会遇到捆绑安装的情况。你明明下载了一个软件,电脑上却多出好几个。那么我们在安装软件时,如何才能避免捆绑安装呢? 什么是捆绑安装?
捆绑安装是指用户安装一个软件时ÿ…