1.图的遍历
按照某种规则沿着图中的边对图中的所有顶点访问一次且仅访问一次。
注:图是一种特殊的树。
1.广度优先遍历BFS
不难看出,图的广度优先就是参照的树的层次遍历算法。
2.深度优先遍历
从某个顶点开始V,访问这个顶点V相邻的任意一个顶点W,在访问W相邻的结点,如此直到没有结点可以访问,依次退回到最近访问的顶点,若它还有邻点未访问则从该点继续重复上述过程,直到图中所有点访问。
2.图的最小生成树
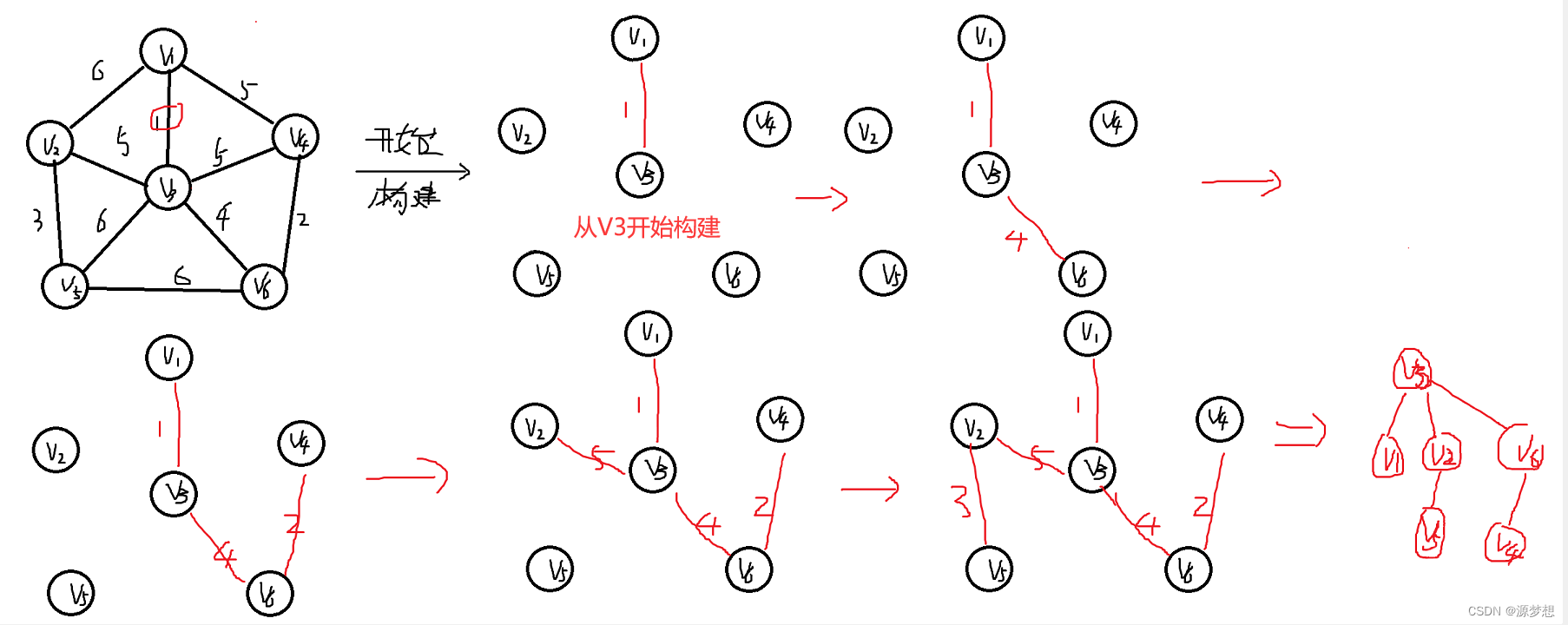
1.Prim算法
从某一个顶点开始构建生成树,每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
注:
1.每次加入新顶点后要连通
2.加入新顶点后不可构成回路
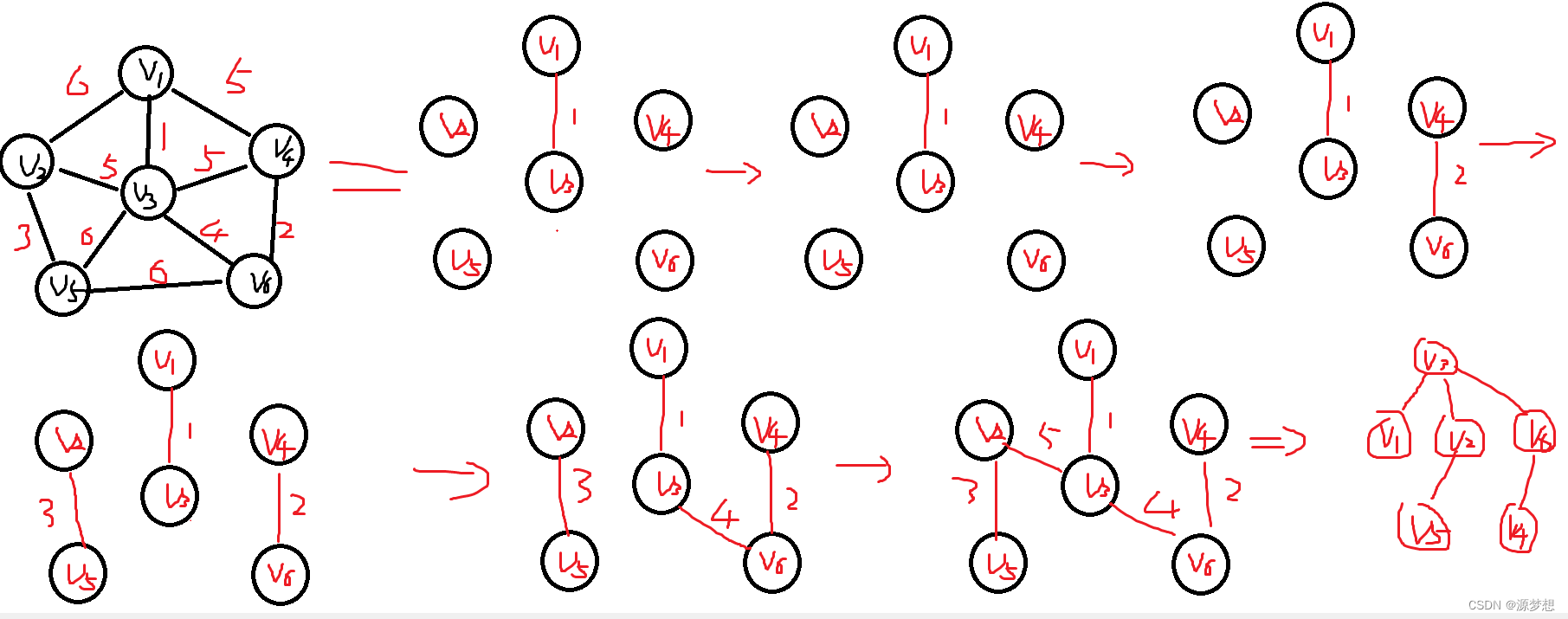
2.Kruskal
每次选择一条权值最小的边,使这条边的两头连通(原本已经连通了不可选)直到所有顶点都连通
注:
1.加入新边后不可形成回路。
3.图的最短路径
1.Dijkstra
final[ ] :标记各顶点是否已找到最短路径
dist[ ] :最短路径长度
path[ ] :路径上的前驱
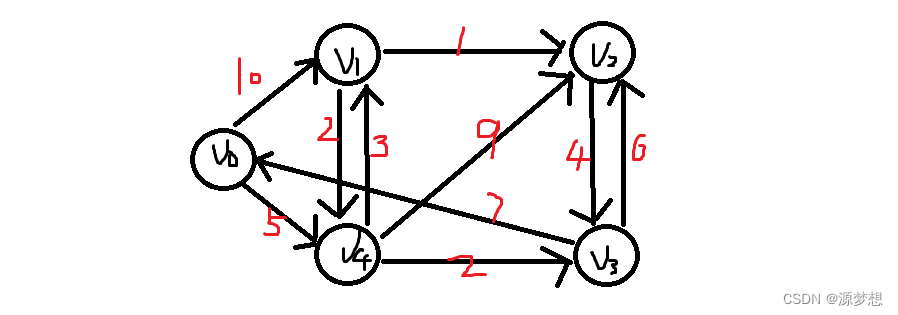
假设从V0出发,则基于V0的情况对三个数组进行初始化:
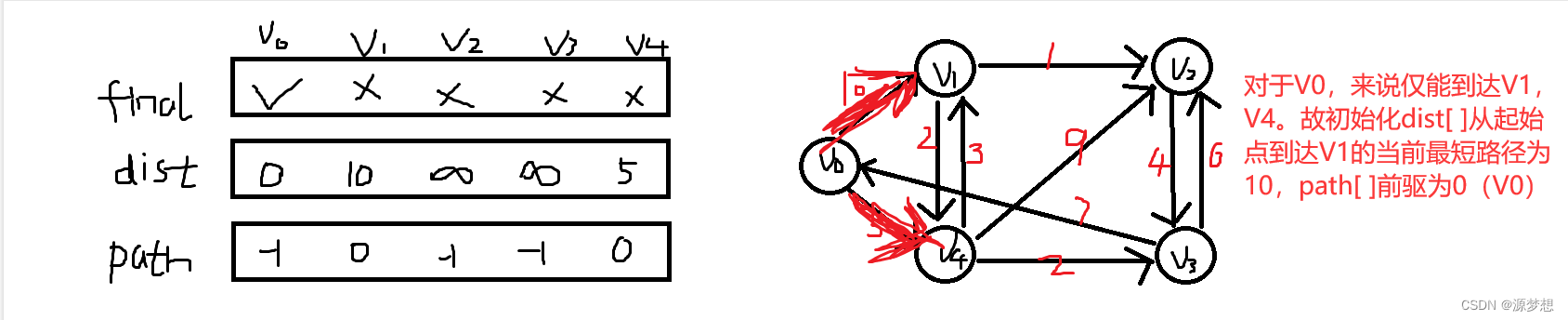
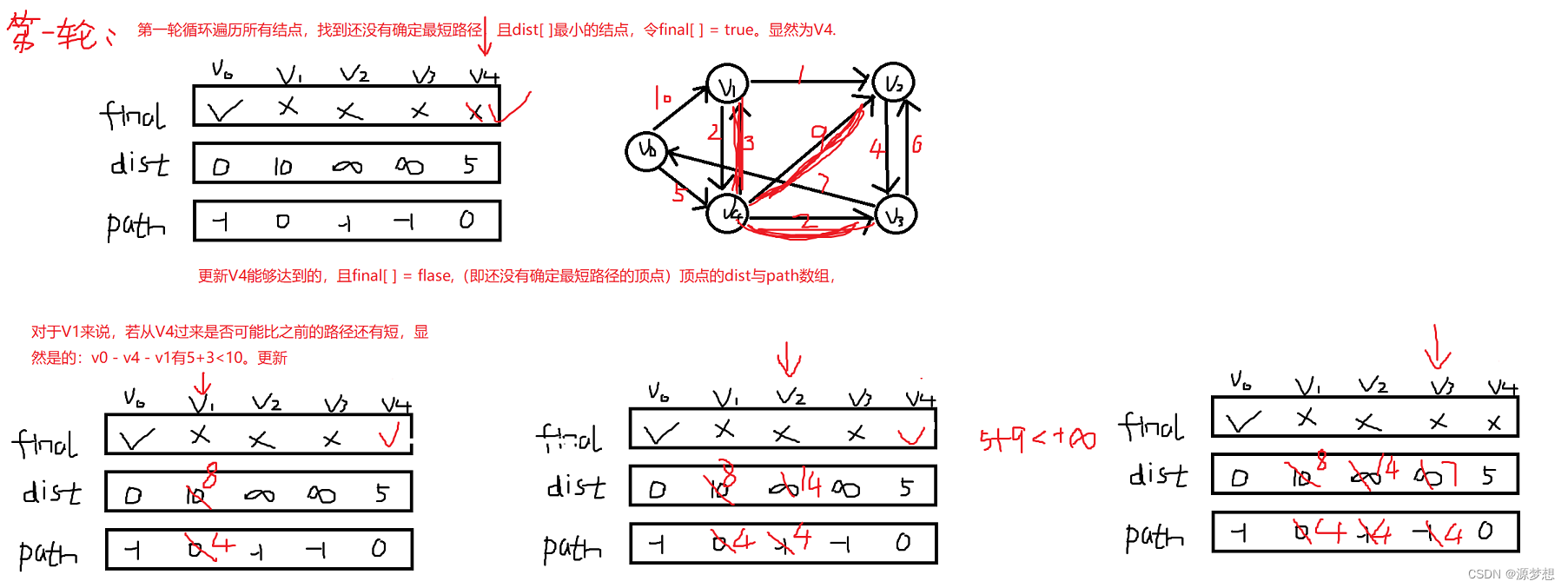
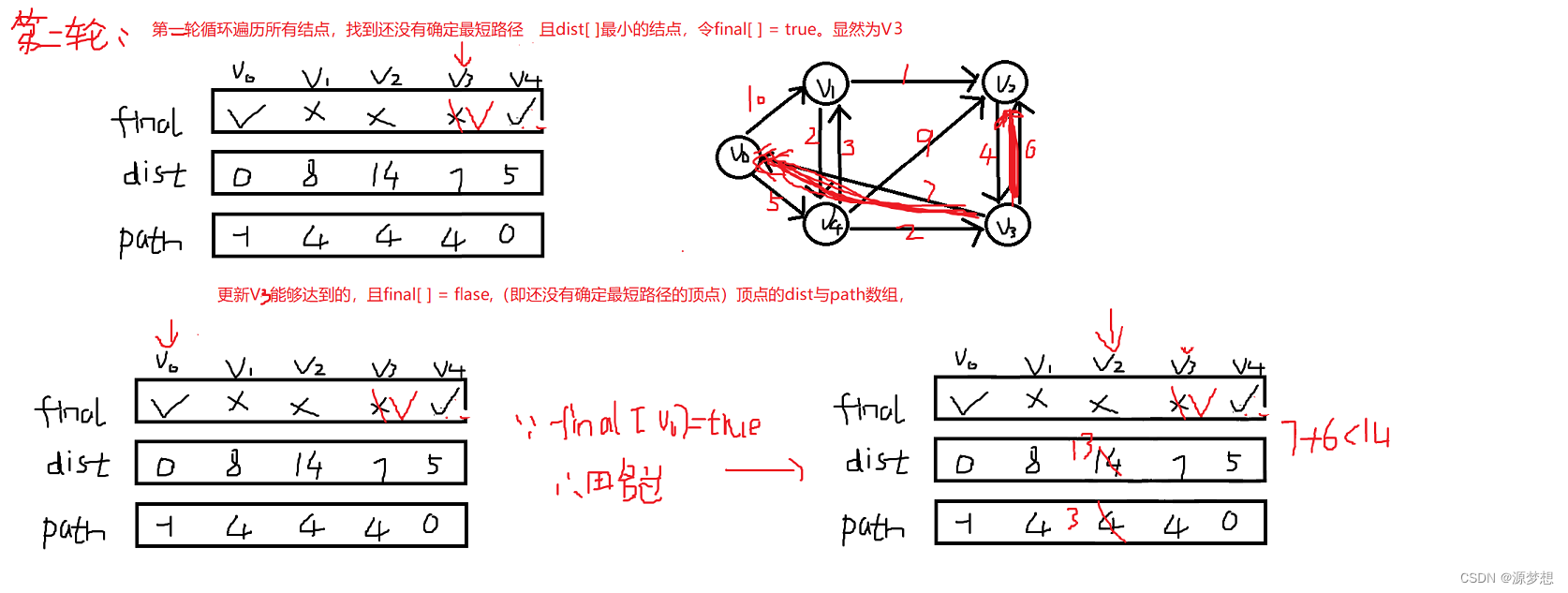
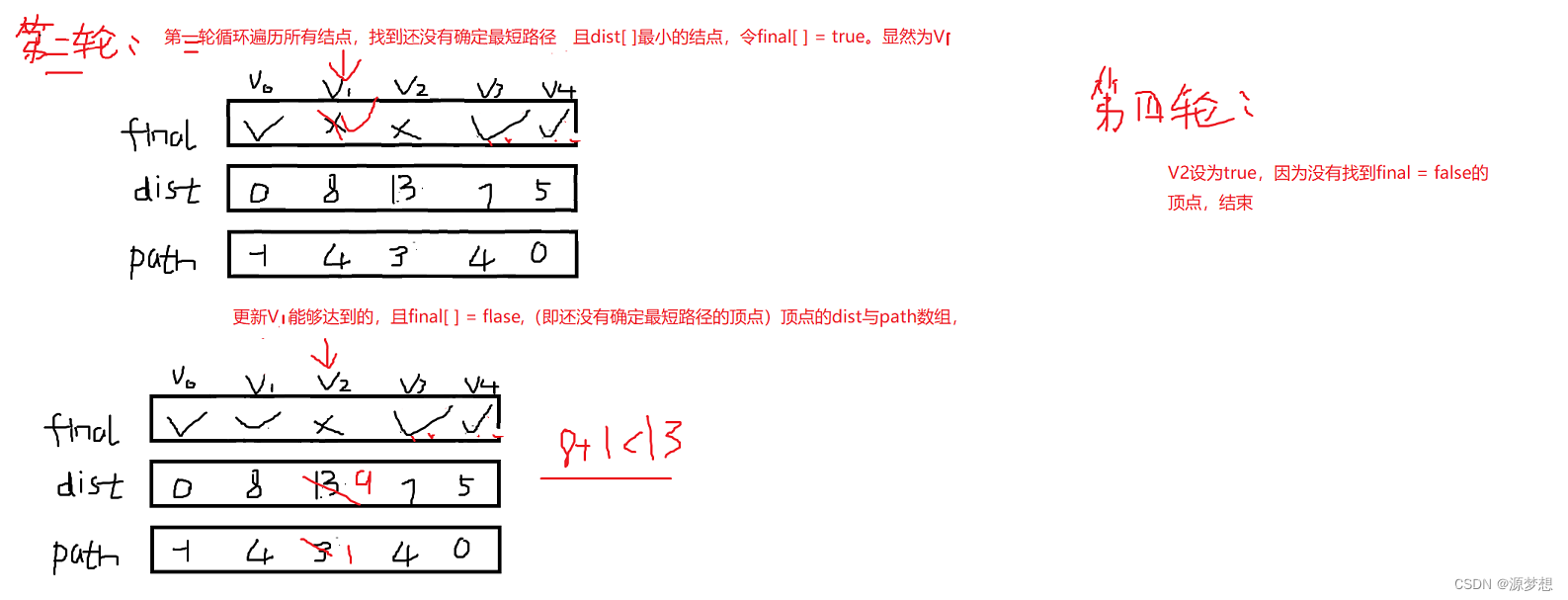
根据dist与path数组,我们可以知道V0点到任意顶点的最短路径,即路径轨迹。
如:V0到V2:V0 -> V4 - > V1 -> V2 且为9
2.Floyd
基于动态规划思想。


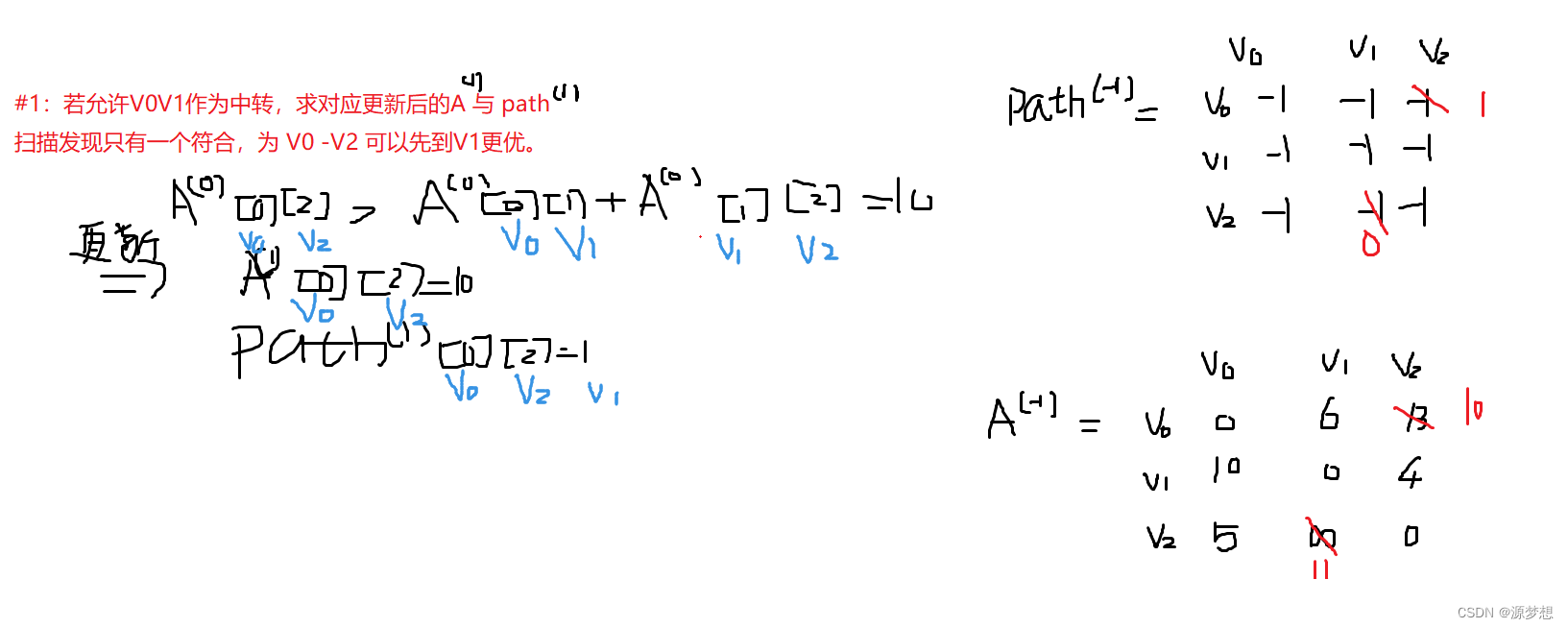
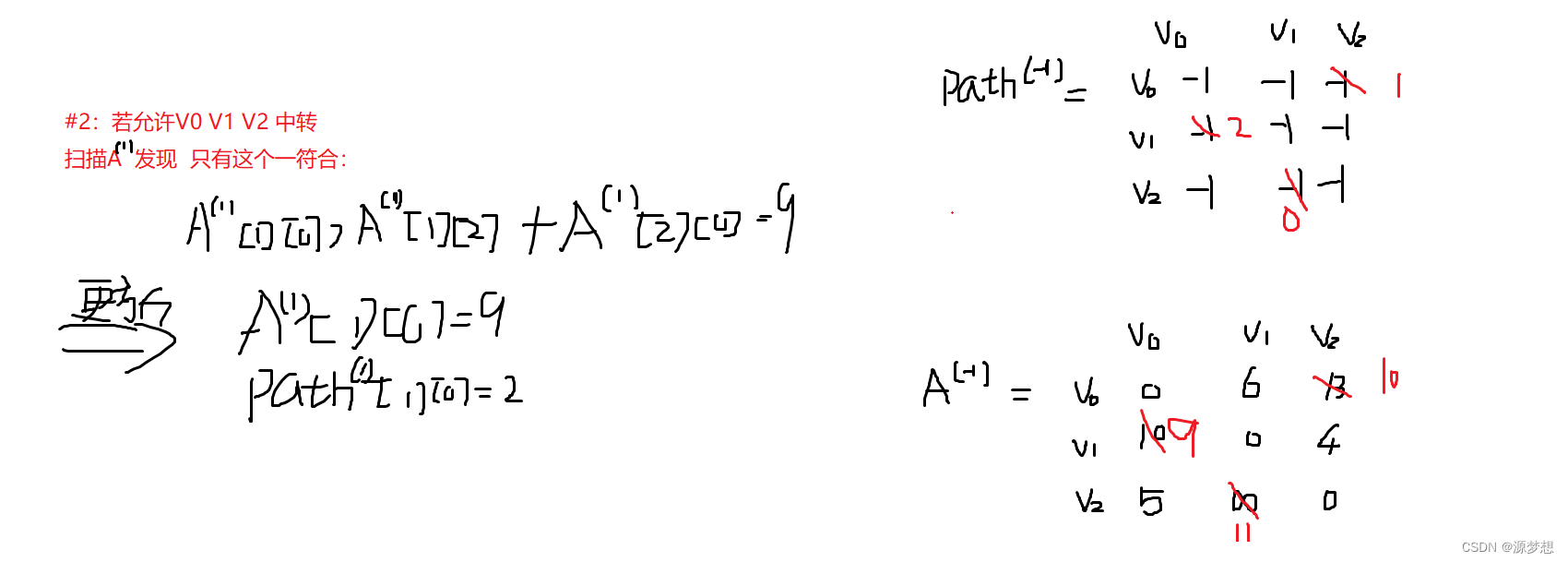

3.BFS
先略。