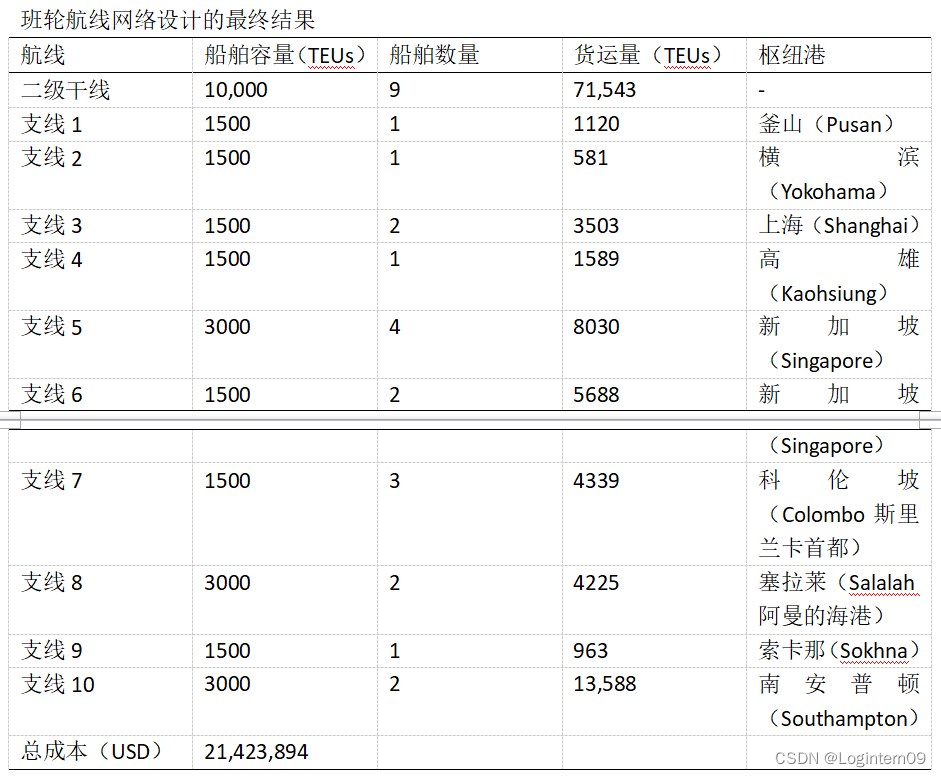
要求解光纤中的电磁场分布，就要构建合适的物理模型

将光纤假设为圆柱状的波导，求解满足均匀原型介质波导边界条件的麦克斯韦方程组，即可

z分量的亥姆霍兹方程为：

对应在圆柱坐标系下为：

用分离变量法求解Ez：

其中R(r)满足的方程可以表示为：

这就是贝塞尔方程。在MATLAB基础操作专栏，有用MATLAB求解贝塞尔方程的方法。

MATLAB仿真贝塞尔函数_matlab练习生的博客-CSDN博客

调用可得到：

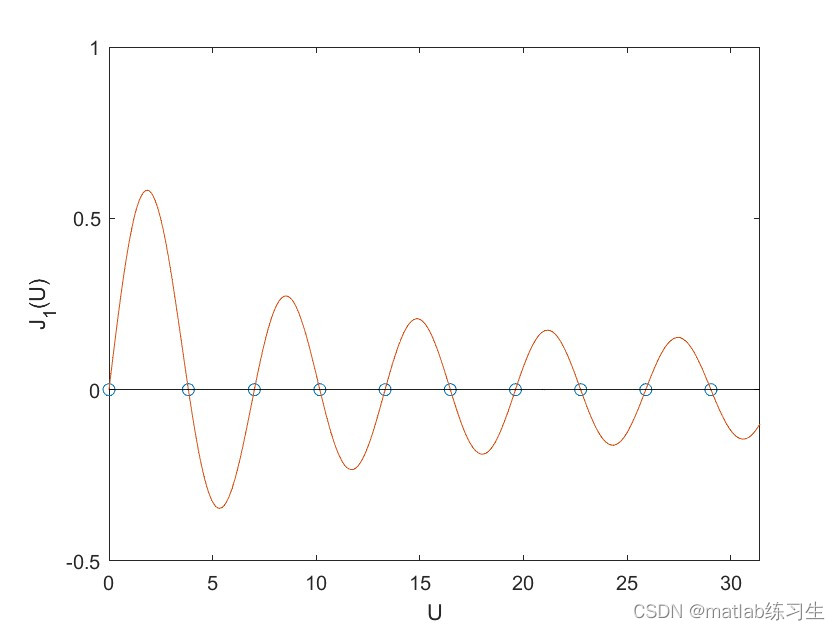
这就是第一类贝塞尔函数的曲线

通过MATLAB求解贝塞尔方程的零点，就是上述方程的解

1阶贝塞尔函数：

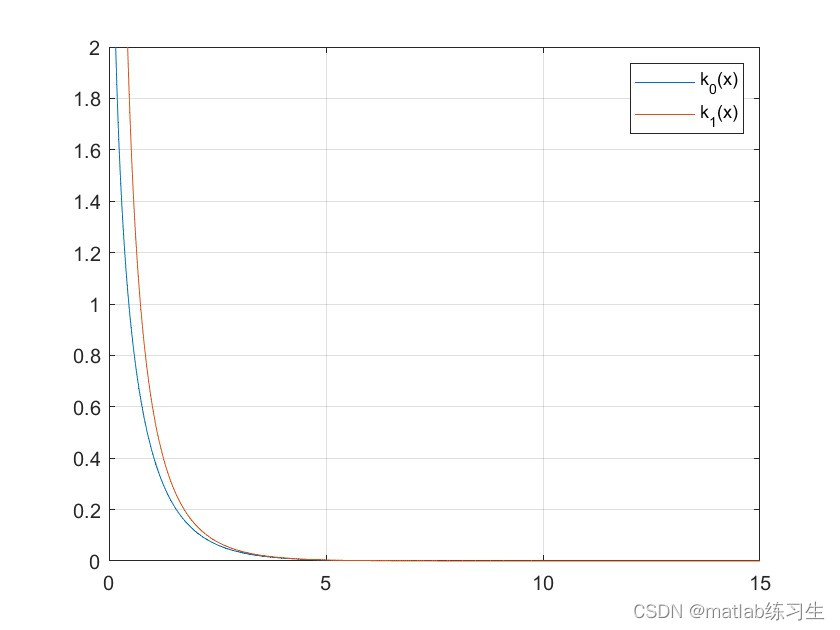
 光纤的芯层区域对应第一类贝塞尔函数，包层区域则对应第二类贝塞尔函数：

事实上，上述方程可以用贝塞尔函数解得：

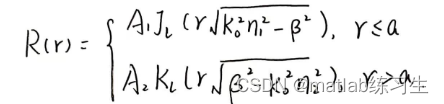
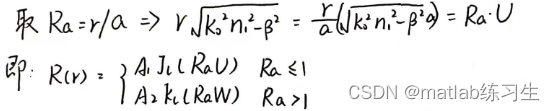
 带入电场的表达式有：

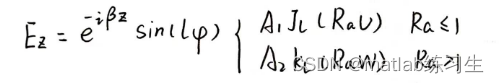
根据边界条件，电场的切向分量在归一化半径坐标Ra=1处应当是连续的，可以解出：

磁场的z分量可以表示为：

根据麦克斯韦方程组解出的各个分量之间的关系，我们可以将电磁场表示出来，

分成芯层和包层两类：

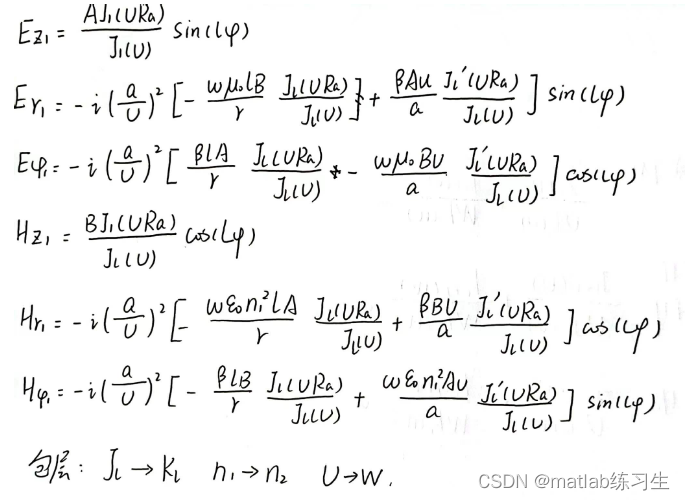
根据实际的物理意义可知，当能够形成导波时，要求UW是正实数，有：

解得：

参考《高等光学仿真——光波导、激光》