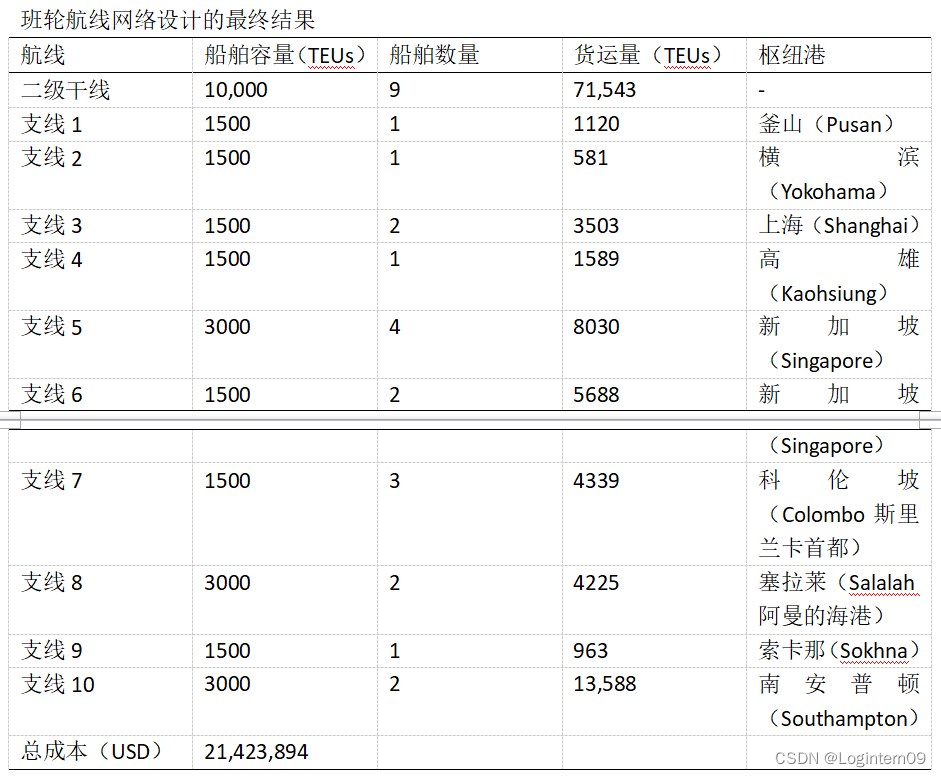
拓扑排序与关键路径是有向无环图上的应用。两种算法使用同一种动态规划的思想，因此关键路径的代码几乎和拓扑排序完全一样。

（一）拓扑排序

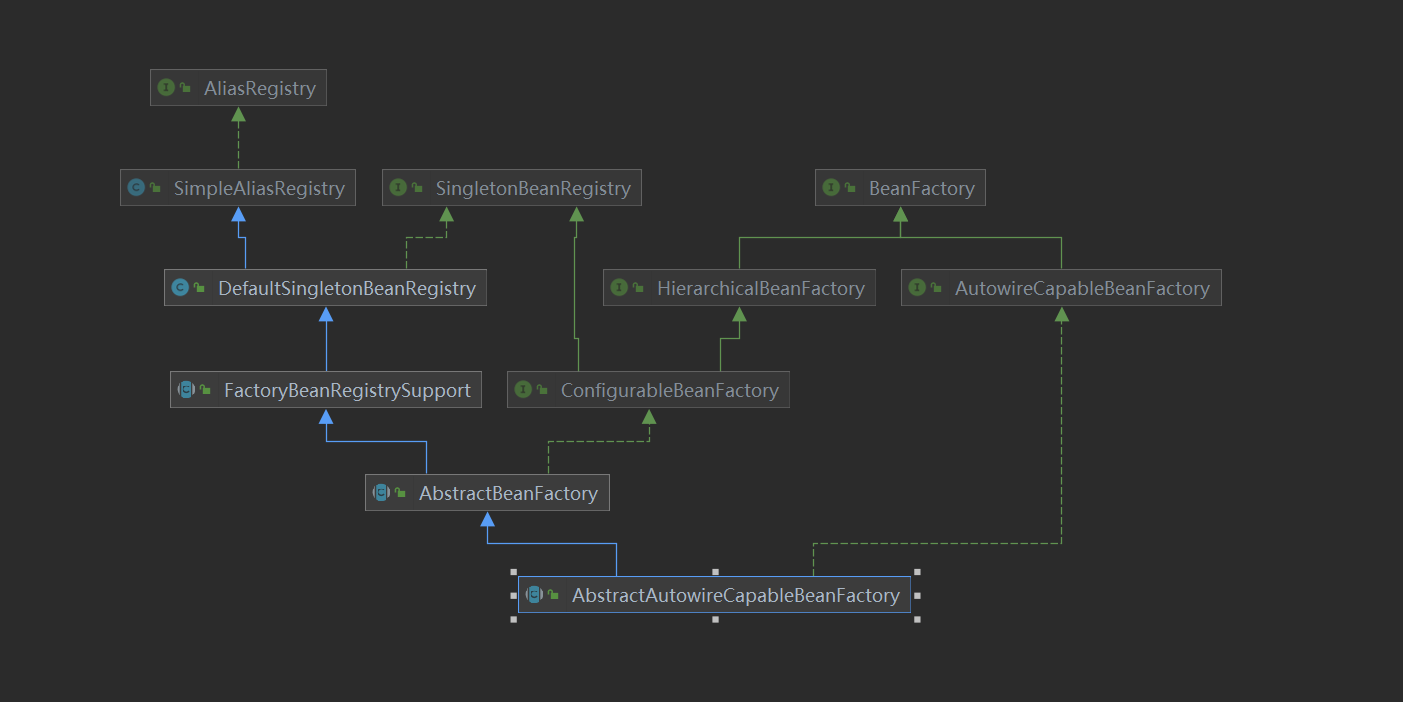
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

拓扑排序的目的是得到一个满足条件的序列，这样的序列可能有多种。如下图拓扑序列就有

C1 , C2 , C3 , C4 , C5 , C6 , C8 , C9 , C7 或      C1 , C8 , C9 , C2 , C5 , C3 , C4 , C7 , C6

另外，存储结构差异（邻接矩阵和邻接表）也可能导致序列不同。

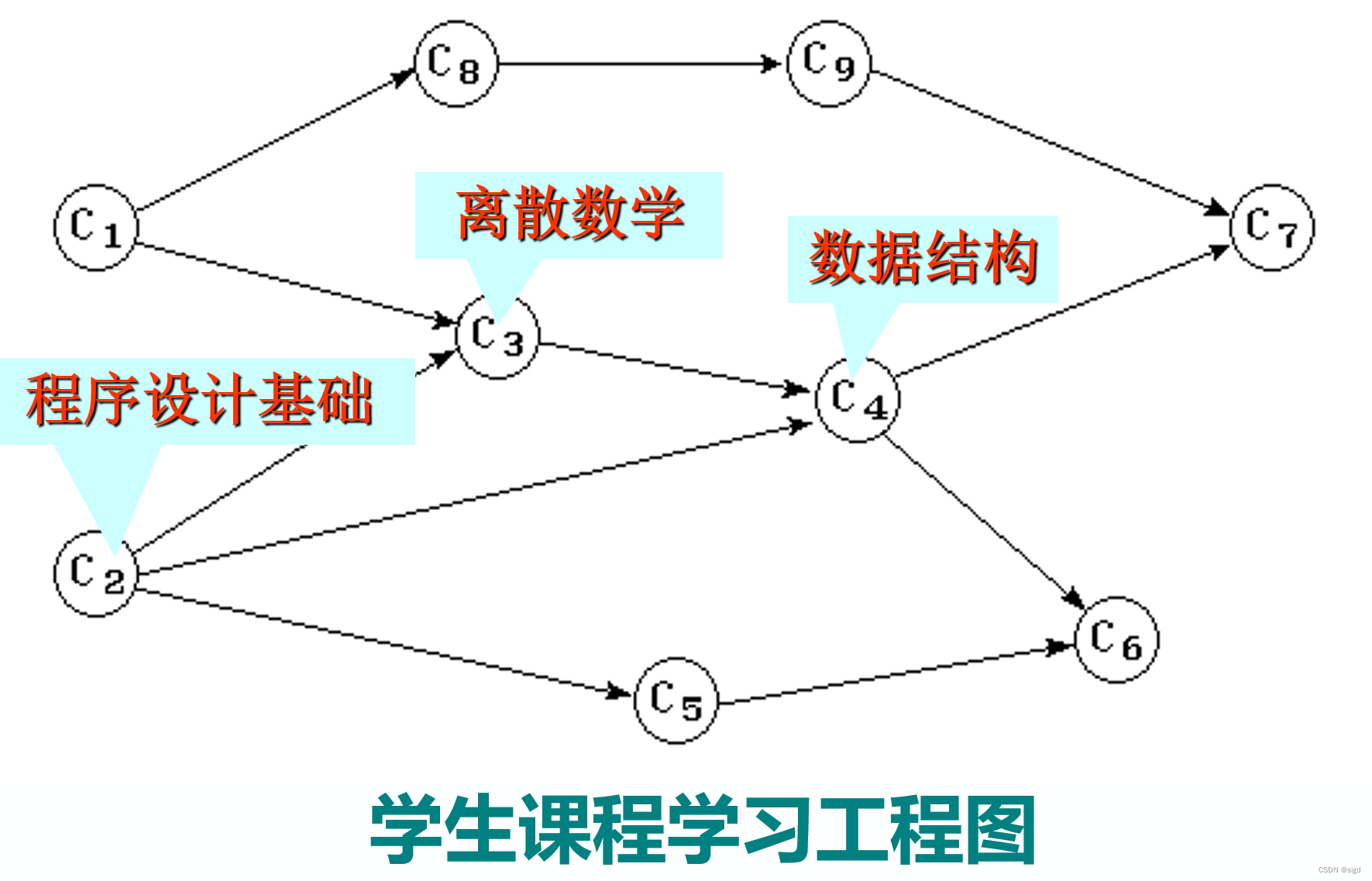
算法实现：要想输出上图C4，必须先输出其前驱结点C2和C3，这实际上是一种动态规划思想。此处采用递推实现，例如输出C2时，将这一信息传递给C2的邻接点C3和C5。为了完成信息传递，使用一个数组d来存储每个点的入度，当结点X的前驱结点Y输出时，将X的入度减一，如果入度减一后为0，那么结点X所有前驱都已经输出，此时X可以输出。通常使用队列（也可以用其他查找结构）来存储这些度为0的结点。下为18734 拓扑排序代码。

#include <iostream>
#include <queue>
using namespace std;
int n,m,e[105][105],d[105];
int main()
{
    int i,j,x,y,z;
    cin>>n>>m;
    for(i=1;i<=m;i++)
    {
        cin>>x>>y;
        e[x][y]=1;
        d[y]++;/**< 统计入度 */
    }
    //int q[1005],f=0,r=0;
    priority_queue<int,vector<int>,greater<int> > q;
    for(i=1;i<=n;i++)/**< 题目要求拓扑序列字典序最小，所以用优先队列存储度为0 */
        if(d[i]==0)
          q.push(i);
    while(!q.empty())
    {
        int t=q.top();
        q.pop();
        cout<<t<<' ';
        for(i=1;i<=n;i++)
            if(e[t][i])
        {
            d[i]--;
            if(d[i]==0)/**< 度为0入队 */
                q.push(i);
        }
    }
    return 0;
}

（二）关键路径

图结构中从起点到终点的最长路径，常用于计算工程项目的最早完成时间。下图起点1到终点6的关键路径（最长路径）为1456。

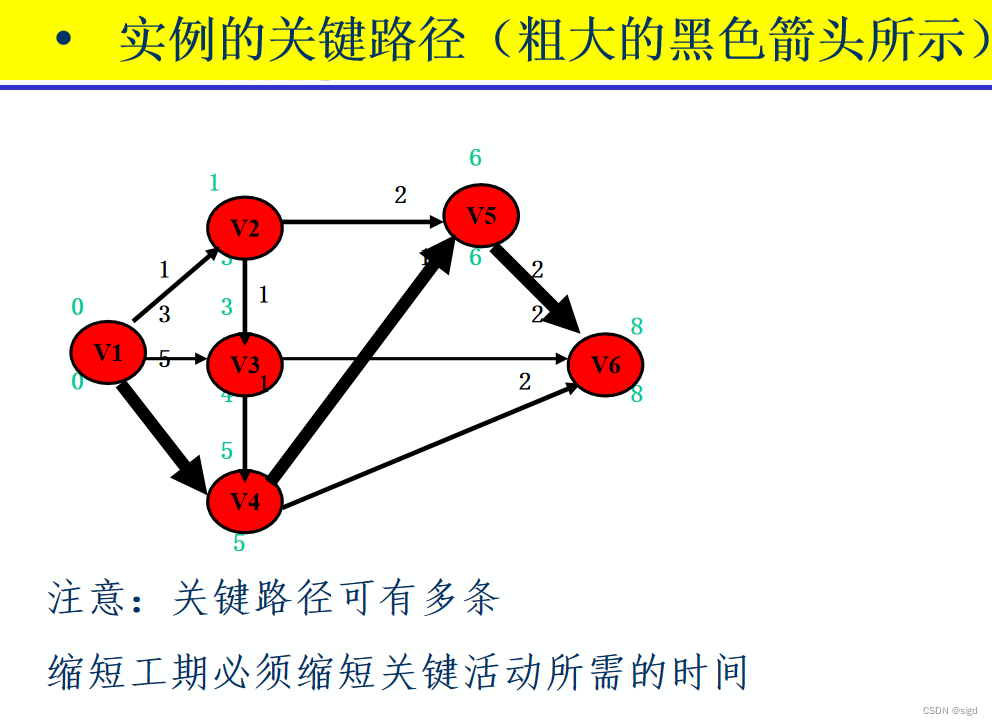
算法思路：如上图V5的路径必须经过V2或V4，因此V5最长路径dis[5]的值由dis[2]和dis[4]决定。

dis[5]=max(dis[2]+(2,5),dis[4]+(4,5)]

算法使用拓扑排序相同的处理过程，在拓扑排序过程中计算最长路径（最早发生事件）。

#include <iostream>
#include <queue>
using namespace std;/**< dis数组记录路径长度 */
int n,m,a[105][105],v[1005],d[1005],dis[1005];
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    int i,j,x,y,z;
    cin>>n>>m;
    for(i=1; i<=m; i++)
    {
        cin>>x>>y>>z;
        a[x][y]=z;
        d[y]++;
    }
    queue<int>q;
    q.push(1);/**< 唯一入度为0的点 */
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        for(i=1; i<=n; i++)
        {
            if(a[t][i])
            { /**< 关键路径和拓扑排序唯一区别在于此处计算最长路径 */
                dis[i]=max(dis[i],dis[t]+a[t][i]);
                d[i]--;
                if(d[i]==0)
                    q.push(i);
            }
        }
    }
    cout<<dis[n];
    return 0;
}

那么如何得到关键路径呢？此处并没有使用教材上的求最迟发生时间的方法。可以借鉴求最短路径的方法，用一个p数组记录前驱结点。

#include <iostream>
#include <queue>
using namespace std;/**< dis数组记录路径长度 */
int n,m,a[105][105],v[1005],d[1005],dis[1005],path[105];
void print(int x)/**< 递归输出最长路径结点序列 */
{
    if(x==0)
        return ;
    print(path[x]);
    cout<<x<<' ';
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    int i,j,x,y,z;
    cin>>n>>m;
    for(i=1; i<=m; i++)
    {
        cin>>x>>y>>z;
        a[x][y]=z;
        d[y]++;
    }
    queue<int>q;
    q.push(1);/**< 唯一入度为0的点 */
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        for(i=1; i<=n; i++)
        {
            if(a[t][i])
            {
                /**< 关键路径和拓扑排序唯一区别在于此处计算最长路径 */
                if(dis[i]<dis[t]+a[t][i])
                {
                    dis[i]=dis[t]+a[t][i];
                    path[i]=t;/**< 记录i的前驱结点为t */
                }
                d[i]--;
                if(d[i]==0)
                    q.push(i);
            }
        }
    }
    //print(n);
    cout<<dis[n];
    return 0;
}