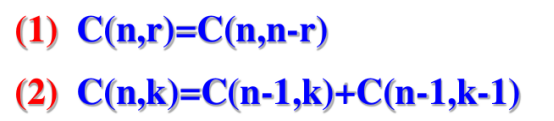1、8个相同的球放进4个相同的盒子里，每盒至少一个，有几种方法 ？
公式：球相同，盒相同，拆分公式。
P4(8)=P1(4)+P2(4)+P3(4)+P4(4)
=1+2+1+1
=5

2、8个相同的球放进4个不同的盒子里，每盒至少一个，有几种方法 ？
公式：球相同，盒不同，插板法。
C(8-1,4-1)
=C(7,3)
=765/6
=35

3、8个不同的球放进4个不同的盒子里，每盒至少一个，有几种方法 ？
公式：球不同，盒不同，不为空，阶乘和二类斯特林数，球是行号，盒子是列号。
M!S(N,M)
=4! * S(8,4)
=241701
=40824

4、8个不同的球放进4个相同的盒子里，每盒至少一个，有几种方法 ？
公式：球不同，盒同，二类斯特林数，为空是累加，不为空是直接取数，球是行号，盒子是列号。
S(N,M)
=S(8,4)
=1701

5、8个相同的球放进4个相同的盒子里，有几种方法 ？
公式：球同，盒同，为空，拆分公式。
P4(8+4)=P4(12)
=P1(8)+P2(8)+P3(8)+P4(8)
=1+4+(P1(5)+P2(5)+P3(5))+(P1(4)+P2(4)+P3(4)+P4(4))
=1+4+(1+2+(P1(2)+P2(2))+(1+2+1+1)
=1+4+5+5
=15

6、8个相同的球放进4个不同的盒子里，有几种方法 ？
公式：球同，盒不同，插板法。
C(11,3)
=11109/6=15*11=165

7、8个不同的球放进4个不同的盒子里，有几种方法 ？
公式：球不同，盒不同，为空，直接是M^N
4⁸⁼⁴44⁴⁼²82^8=256*256=65536

8、8个不同的球放进4个相同的盒子里，有几种方法 ？
公式：球不同，盒同，二类斯特林数，为空，是累加
S (N, 1) + S(N, 2) + S(N, 3) + … + S(N, M)
=S（8,1)+S（8,2)+S（8,3)+S（8,4)
=1+127+966+1701
=2795

9、8个不同的球平均分给4个小朋友，有几种分法 ？
从8个球中取2个分给第1个小朋友，从剩下6个中取2个来分给第二个小朋友。。。
C(8,2)*C(6,2)*C(4,2)*C(2,2) = 2520

10、8个不同的球平均分成4堆，有几种分法 ？
C(8,2)*C(6,2)*C(4,2)*C(2,2) / 4!= 2520/24 =105