1 Automatic Extrinsic Calibration Method for LiDAR and Camera Sensor Setups 2022

vel2cam
git

2 A Novel Method for LiDARCamera Calibration by PlaneFitting

本文介绍了一种使用带ArUco标记的立方体的3D-3D对应特征来校准LiDAR和相机的新方法。在LiDAR坐标系中，选择三个表面上的点数据分别拟合平面方程。通过这种方式，可以获得每个平面的顶点坐标和法向量。在相机坐标系中，通过相机的完整6D姿态估计使用ArUco标记可以获得每个平面对应点的坐标和法向量。通过上述数据，可以获得每个传感器的一组点云，然后可以使用Kabsch算法[1]计算刚性变换。实验表明，我们的方法可以获得比现有方法（Ankit的方法）更稳定的校准结果，并且不会损失精度。

介绍

传统机器只能执行一些简单的工作。我们必须通过将传感器集成到系统中来赋予它们理解环境的能力，使它们变得更加智能。随着传感器技术的发展，许多种类的传感器现在被用于自动驾驶、工业设备、SLAM等领域[2]，[3]。每种传感器都有其优点和缺点。广泛使用的2D传感器，如CCD和CMOS，最重要的优点是图像包含颜色、纹理和几何信息。因此，相机在人、脸、交通信号灯等物体检测方面非常重要和有用。然而，相机受光线条件和天气影响很大。

3D传感器可以获取环境的点云数据等3D数据。它们可以根据有效距离分为两种。如微软Kinect、英特尔RealSense和华硕Xtion Pro等RGBD相机，其有效距离非常短，通常在四米内。英特尔RealSense R200的有效距离为0.51-4米。最新的RealSense深度相机D435根据校准、场景和光照条件的不同，最远有效距离约为10米。华硕Xtion Pro的有效距离为0.8-3.5米。ZED使用双目视觉，其有效距离为0.5至20米。然而，它依赖于NVIDIA GPU，并消耗大量计算机资源，因为ZED相机需要实时计算其两个RGB传感器捕获的两个图像并输出点云数据。因此，它也受光线条件和低能见度以及所有其他图像传感器的影响。长距离传感器主要是指激光雷达（LiDAR）。LiDAR系统基于飞行时间法来确定LiDAR和物体之间的距离。它是可靠、快速的，有效距离可高达200-300米。有许多LiDAR制造商，如Velodyne、Hesai、Ibeo等。它们的产品可以按通道或环数分为不同类型。单信道LiDAR只能扫描平面，因此非常适合所有种类的服务机器人来检测墙、桌子、椅子等。多通道LiDAR可以获取更多环境信息，因此在汽车和其他行业场景中更广泛地使用。RGBD相机可以收集2D和3D信息。但是，它的有效距离限制了其应用。LiDAR非常有用，但只能收集有关环境的3D距离信息。相机可以获得许多其他信息，如颜色、纹理和几何信息。但是，它不能收集3D信息，并且受光线条件和天气影响很大。为了增加有效距离并收集更多信息使机器更加稳定，常常将LiDAR和相机整合起来以发挥各自的优势。在这种情况下，数据是相对于每个传感器的参考坐标系进行测量的。它们应转换为某个参考坐标系以实现数据合并[4]。因此，校准LiDAR和相机以获取准确的环境测量非常重要。

相关方法

随着激光雷达的广泛应用，特别是在自动驾驶汽车领域，许多研究人员尝试对LiDAR和相机进行校准。估计平移和旋转参数的基本步骤是最小化在2D空间或3D空间中对应特征之间的距离。大多数校准方法可以分为2D-3D方法或3D-3D方法。这两种方法都需要先校准相机以获取相机坐标系中的准确坐标。

2D-3D方法中，相机特征直接在图像中检测。LiDAR特征在三维空间中检测，并使用相机矩阵投影到图像平面上。对应特征之间的距离被最小化以估计刚体变换。特征可以是点、校准器的边缘或平面。这种方法广泛使用，因为可以通过图像处理轻松地搜索特征。不同的校准器用于适应不同数量的LiDAR通道，根据校准器使用不同种类的特征。Liu和Yang使用V形校准器进行摄像机和单行扫描LiDAR的校准。由于单行扫描LiDAR使用红外光源，可以被红外相机捕捉，因此使用相机和红外滤镜直接观察LiDAR光束。通过这种方式，收集一组对应点（至少4个）以计算LiDAR和相机坐标系之间的刚体变换。Kiho Kwak等人使用类似的V形校准器，利用红外相机直接观察LiDAR光束，并使用不同的特征。然而，必须在一次校准中多次放置校准器以获得足够的数据。更常见的情况是在图像和LiDAR点云中分别检测校准器上的特征点。Xu和Li使用具有水平矩形孔的板作为校准器，将孔边缘附近的两个LiDAR点用于估计边缘上的中心点作为特征点。由于在边缘上替换点与两个其他点的中点之间的水平误差是不可避免的。使用球校准不同的LiDAR和相机，球面上被击中的LiDAR点被用来拟合球体以确定球心位置作为特征点。由于球只能提供一个特征点（球心），因此需要将球放置在多个位置，以获得足够的对应点。在我们的方法中，建议使用立方体作为校准器，可以仅使用一个帧数据获得足够的特征点。

3D-3D方法需要在三维空间中检测LiDAR和相机的对应特征。在获得相机内参数后，可以使用相机的外部参数将图像平面上的二维点投影到相机坐标系中的三维空间，并直接检测LiDAR中的特征或拟合三维空间中的线条和平面。这种方法需要额外的校准器，如棋盘或ArUco标记，以获取三维特征。

一种使用 3D-3D 对应点的方法由 Ankit Dhallet 等人提出9，ArUco 标记被粘贴在校准板上，以确定相机与标记之间的外部参数。通过这种方式可以获取相机坐标系中的特征点。通过拟合校准板边缘的线条确定 LiDAR 坐标系中对应点的位置。为了使用 Kabsch 算法计算刚体变换，特征点在相机坐标系和 LiDAR 坐标系中必须相同。提取边缘点和拟合线条方程时引入了额外的误差。此外，只使用了很少的点用于拟合线条方程，使得线条方程的可靠性更低。一个带 4 个圆形孔的板被用作校准标定器，用于校准立体相机和 16 层 LiDAR-（3），检测孔附近的边缘点以适应 LiDAR 点云和立体点云中的圆。三维空间中圆的中心点被用作特征点来估计刚体变换。为了拟合线或圆方程，需要提取一些边缘点[3，9]。但是，边缘点可能无法准确确定，这会导致严重的精度下降。

在本文中，我们提出了一种新的方法，使用带有 ArUco 标记的立方体作为标定器。在 LiDAR 和相机的 3D 空间中检测特征点。除了其他方法中的线拟合外，更多的点被用于拟合平面以减小误差。此外，该方法不依赖于边缘点，因此避免了额外的误差。实验表明，与现有方法（Ankit 的方法）相比，我们的方法可以获得更稳定的校准结果而不损失精度。

方法

为了利用 LiDAR 坐标系中更多的点以减少误差，使用立方体作为标定器，并使用属于每个平面的点来拟合平面方程。此外，立方体可以提供许多特征，使得在校准过程中不必移动标定器。我们还实现了 Ankit 的方法作为参考。标定器我们制作了两种标定器。Ankit 方法所用的标定器是两个 Yakeli 制成的 48 cm × 48 cm 正方形板，上面贴有 ArUco 标记。即使一个校准板就足以获取四个特征点，但为了减小误差，使用了两个板。我们方法所用的标定器是一个 40cm × 40cm × 40cm 的立方体，在三个表面上各有三个 ArUco 标记，如图1所示。相机坐标系中的3D点坐标对于两种方法，3D点的获取方式在相机坐标系中是相同的。我们可以使用 ROS 中的 aruco_ros 和 aruco_mapping 包获取相机相对于 ArUco 标记的姿态。然后将点的坐标转换为相机坐标系。

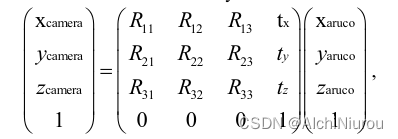
其中，xcamera 是相机坐标系中的坐标，xaruco 是 ArUco 标记坐标系中的坐标，矩阵是相机相对于 ArUco 标记的6D姿态转换而来。

对于线拟合方法，使用两个板作为标定目标，在相机和 LiDAR 坐标系中提供特征点。将板的四个角作为对应点。由于 ArUco 标记的大小和位置是已知的，可以确定角点在 ArUco 标记坐标系中的坐标。然后可以通过公式（1）计算出相机坐标系中的角点坐标。我们还使用两个板来获取八个对应点以减小误差。

对于平面拟合方法，使用三个 ArUco 标记来减小手动粘贴 ArUco 标记带来的误差。可以通过与线拟合方法相同的方式获取顶点的3D坐标。我们使用由 ArUco 标记提供的姿态获取顶点的坐标，可以计算出一个平均坐标。平均坐标与单独获取的坐标几乎相同。

图1. 线拟合方法和平面拟合方法中使用的标定器。ArUco 标记被贴在标定目标上。aruco_mapping 包提供了相机相对于 ArUco 标记的完整6D姿态。由于特征点在 ArUco 标记坐标系中的位置已知，可以使用相机的姿态计算出相机坐标系中特征点的三维坐标。

对于线拟合方法，所有标定板的边缘点都被提取并投影到图像中。应手动选择属于每个边缘的点以拟合边在板子上的三维空间直线方程。采用RANSAC算法来拟合线方程，如图2所示。两条线公共垂线的中点被认为是角点，可以作为LiDAR坐标系下相应点使用。

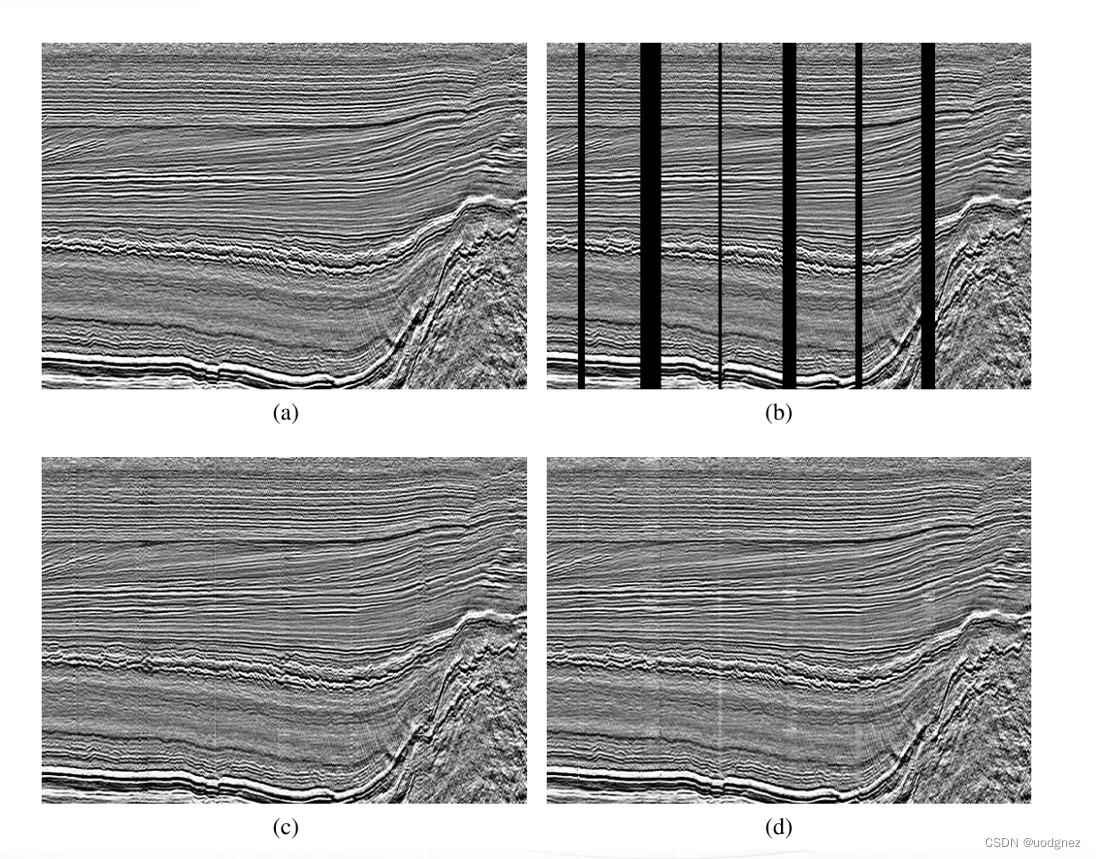
如图3所示，靠近边缘（白色框中的红色点）的点可能远离平面，但是板子中心的点（绿色和靛蓝色）只存在于有限距离内，因此使用中心点比使用边缘点更可靠。此外，由于LiDAR点云在水平方向上也很疏，因此准确提取边缘点是不可能的。因此，在拟合线方程时仅使用少数点。本文中，我们制作了一个立方体标定器，并使用命中表面的点来拟合平面。通过这种方式，我们可以利用更多的点进行误差减小，也避免了在边缘点检测过程中的误差。实验证明，平面法向量的变化小于线法向量的变化。

对于平面拟合方法，手动选择属于三个平面的LiDAR点，如图4所示，使用最小二乘法分别拟合每个平面的方程。然后通过求解方程组获得顶点的坐标。最后，可以使用每个平面的法向量和顶点坐标获得四个相应点。

为了确定相机和LiDAR之间的变换，对这些相应点进行PnP算法求解。