DS：基于鸢尾花数据集利用多种数据降维技术(PCA、SVD、MDS、LDA、T-SNE)实现三维可视化

目录

基于鸢尾花数据集利用多种数据降维技术(PCA、SVD、MDS、LDA、T-SNE)实现三维可视化

# 1、加载示例数据集（鸢尾花数据集）

# 2、数据预处理

# T1、PCA降维

# T2、SVD降维

# T3、MDS降维

# T4、LDA降维

# T5、T-SNE降维

# 3、三维图可视化

原始数据

# T1、PCA降维可视化

# T2、SVD降维可视化

# T3、MDS降维可视化

# T4、LDA降维可视化

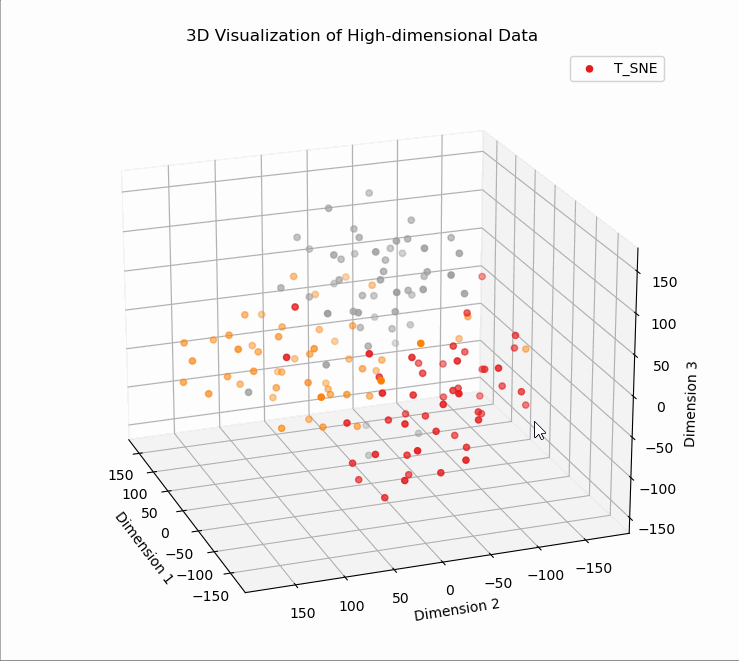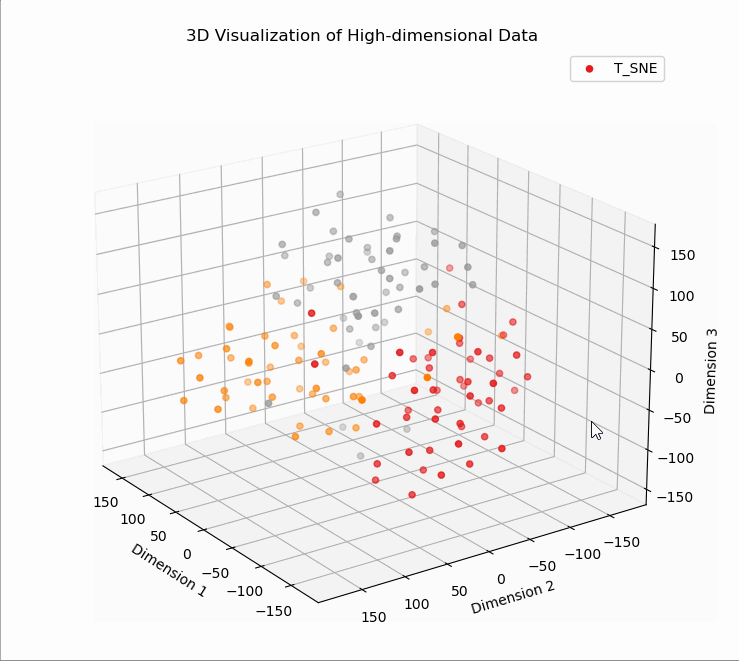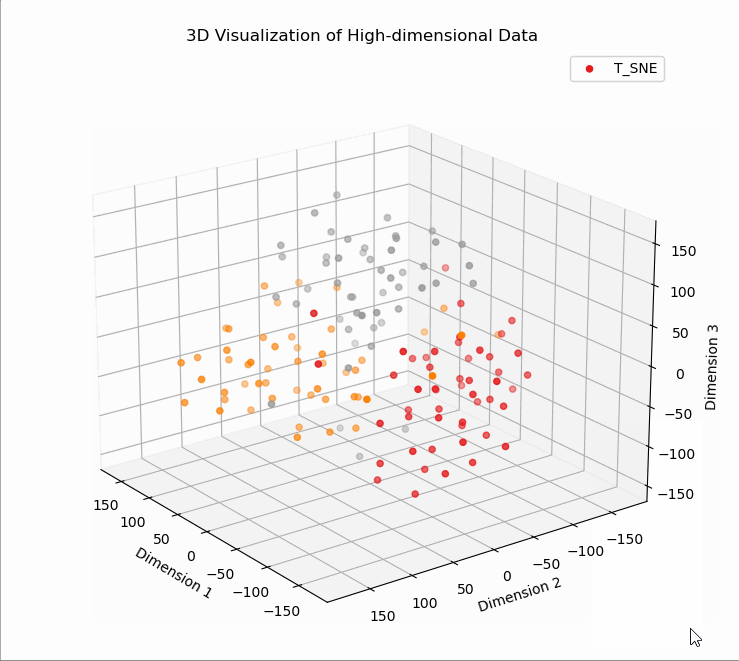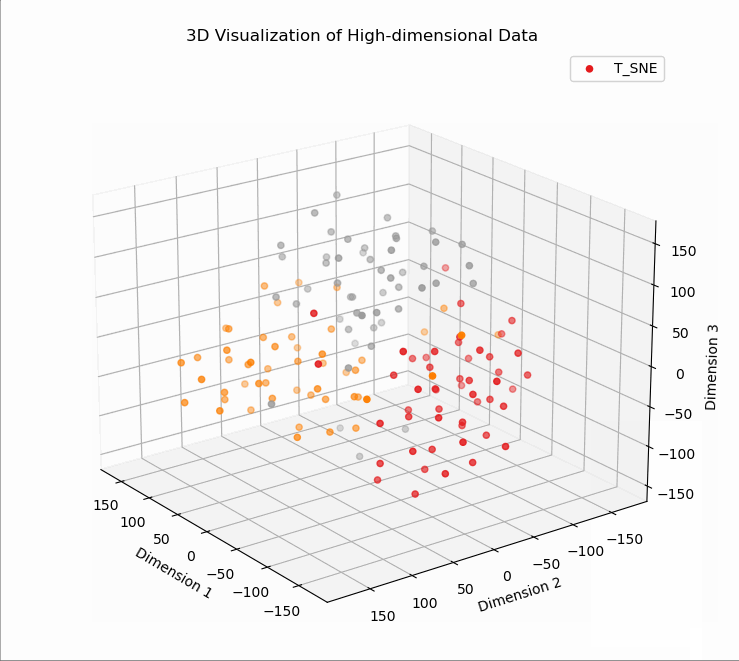
# T5、T-SNE降维可视化

---

相关文章
DS：基于鸢尾花数据集利用多种数据降维技术(PCA、SVD、MDS、LDA、T-SNE)实现三维可视化
DS：基于鸢尾花数据集利用多种数据降维技术(PCA、SVD、MDS、LDA、T-SNE)实现三维可视化实现代码

基于鸢尾花数据集利用多种数据降维技术(PCA、SVD、MDS、LDA、T-SNE)实现三维可视化

# 1、加载示例数据集（鸢尾花数据集）

X_arr (150, 4) 
 [[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
……
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]

# 2、数据预处理

# T1、PCA降维

X_pca (150, 3) 
 [[-2.68412563  0.31939725 -0.02791483]
 [-2.71414169 -0.17700123 -0.21046427]
 [-2.88899057 -0.14494943  0.01790026]
……
 [ 1.90094161  0.11662796  0.72325156]
 [ 1.39018886 -0.28266094  0.36290965]]

# T2、SVD降维

X_svd (150, 3) 
 [[ 5.91274714e+00  2.30203322e+00 -7.40153559e-03]
 [ 5.57248242e+00  1.97182599e+00 -2.44592251e-01]
 [ 5.44697714e+00  2.09520636e+00 -1.50292625e-02]
……
 [ 9.10559876e+00 -9.96415757e-01  7.37102889e-01]
 [ 8.49037542e+00 -9.15931258e-01  3.31393992e-01]]

# T3、MDS降维

X_mds (150, 3) 
 [[ 5.64777636e-02 -2.59570066e+00  7.61545625e-01]
 [-5.99309712e-02 -2.72139473e+00  2.42378810e-01]
 [ 1.77952704e-01 -2.86687262e+00  3.47890436e-01]
……
 [ 6.83493773e-01  1.85739079e+00 -4.80778427e-01]
 [ 2.15716983e-01  1.30234420e+00 -6.37089821e-01]]

# T4、LDA降维

n_component_LDA = 2

X_lda (150, 2) 
 [[ 8.06179978e+00  3.00420621e-01]
 [ 7.12868772e+00 -7.86660426e-01]
……
 [-4.96774090e+00  8.21140550e-01]
 [-5.88614539e+00  2.34509051e+00]
 [-4.68315426e+00  3.32033811e-01]]

# T5、T-SNE降维

X_tsne (150, 3) 
 [[-6.37121058e+00  2.02727718e+01  5.03279305e+01]
 [-8.83170776e+01 -2.08327026e+01  8.66149445e+01]
 [-2.88652115e+01 -5.99451447e+01  1.27320602e+02]
……
 [ 5.76065979e+01 -8.55675659e+01  7.04603043e+01]
 [ 8.31780052e+00 -7.34811707e+01 -1.66465416e+01]]

# 3、三维图可视化

原始数据

# T1、PCA降维可视化

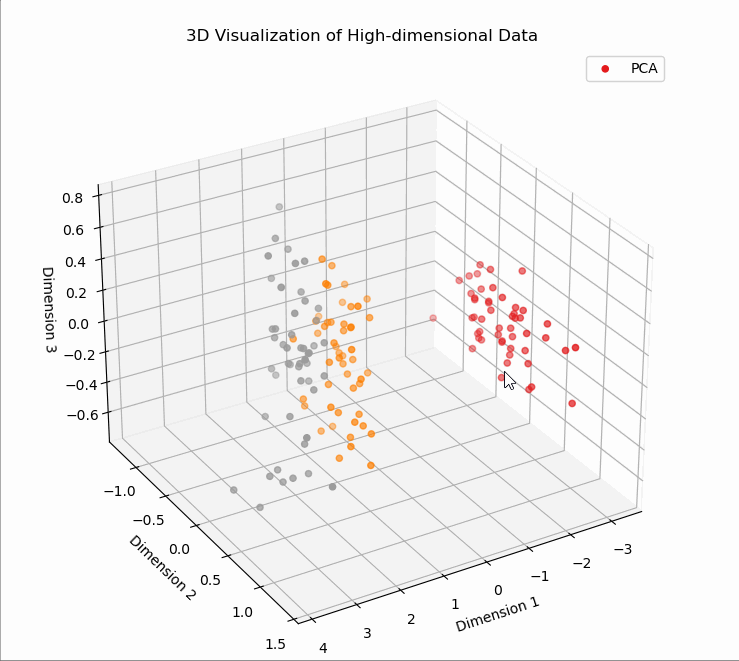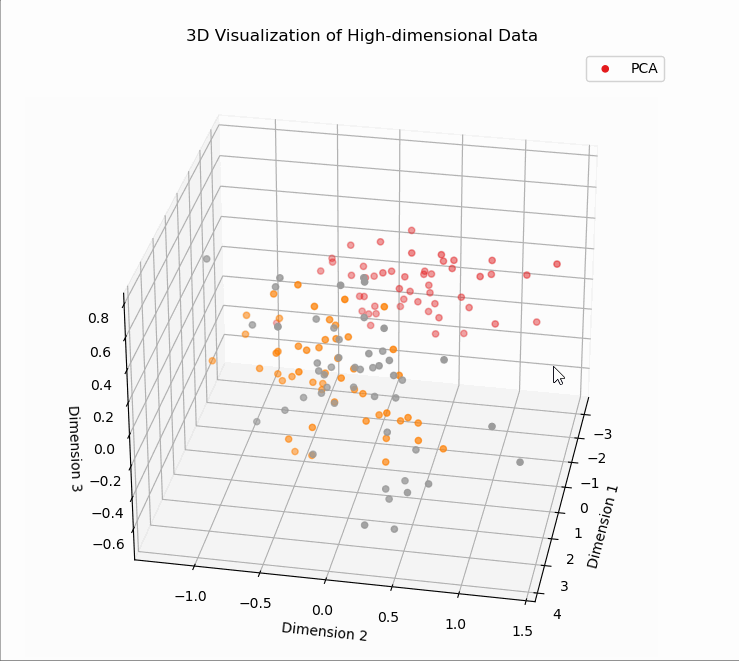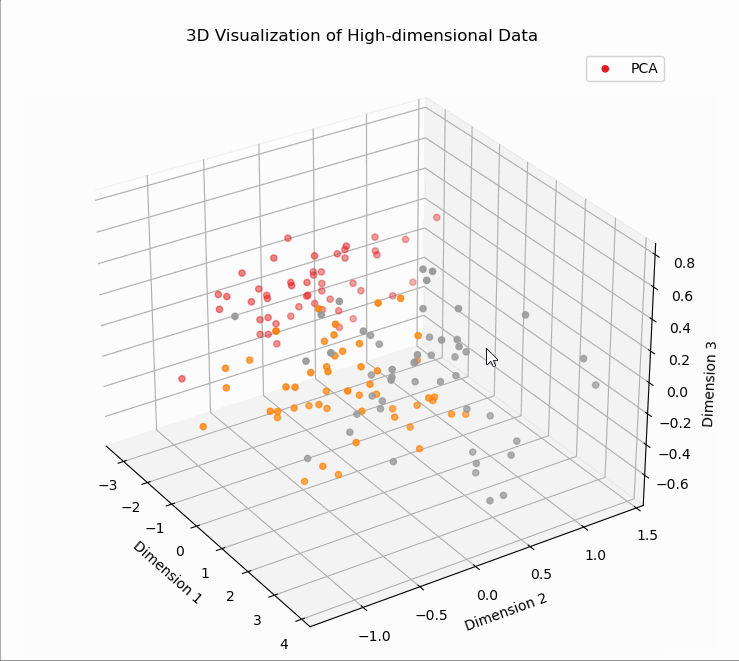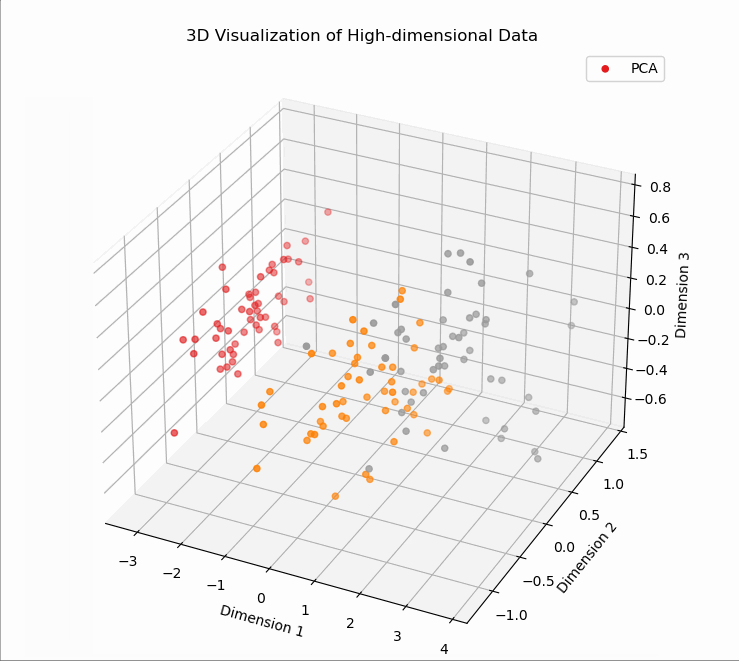
# T2、SVD降维可视化

# T3、MDS降维可视化

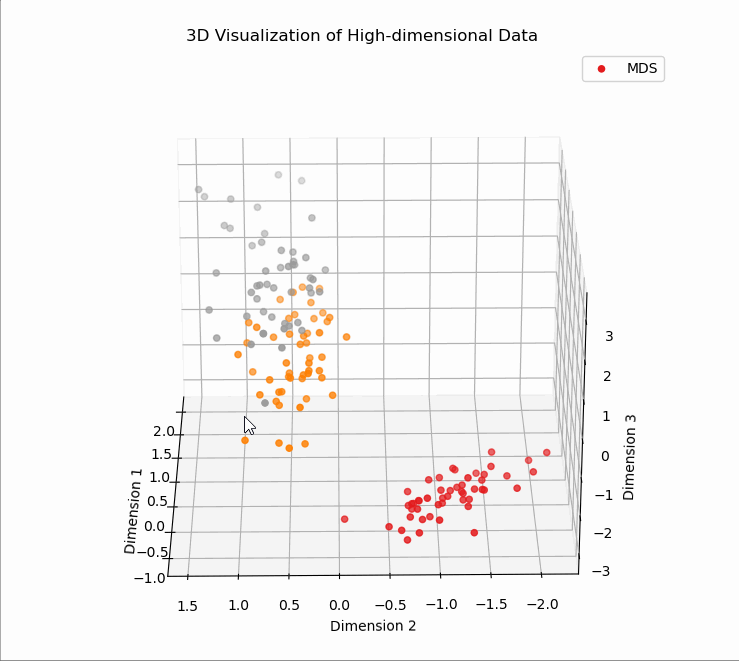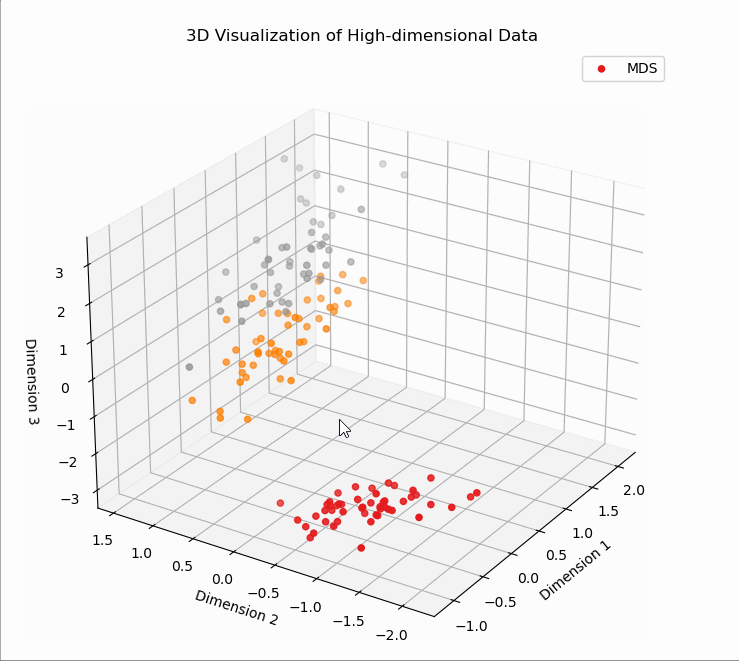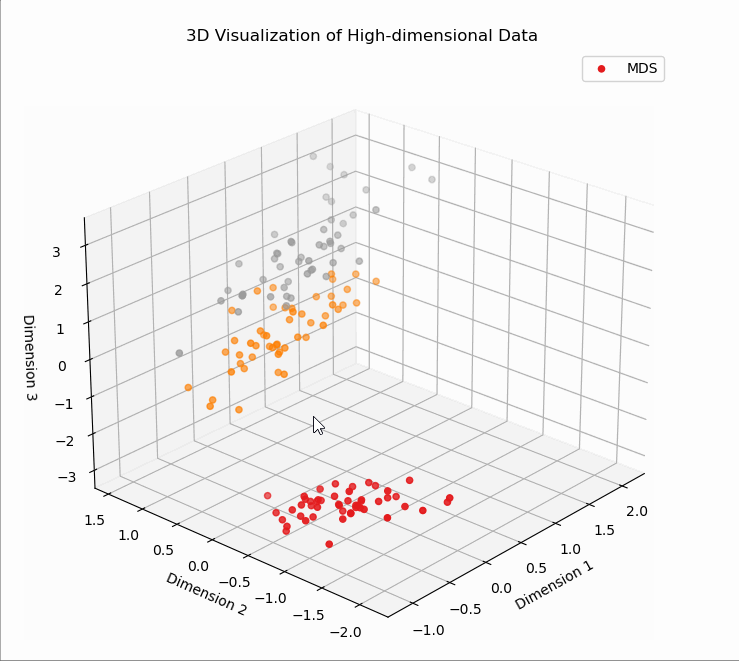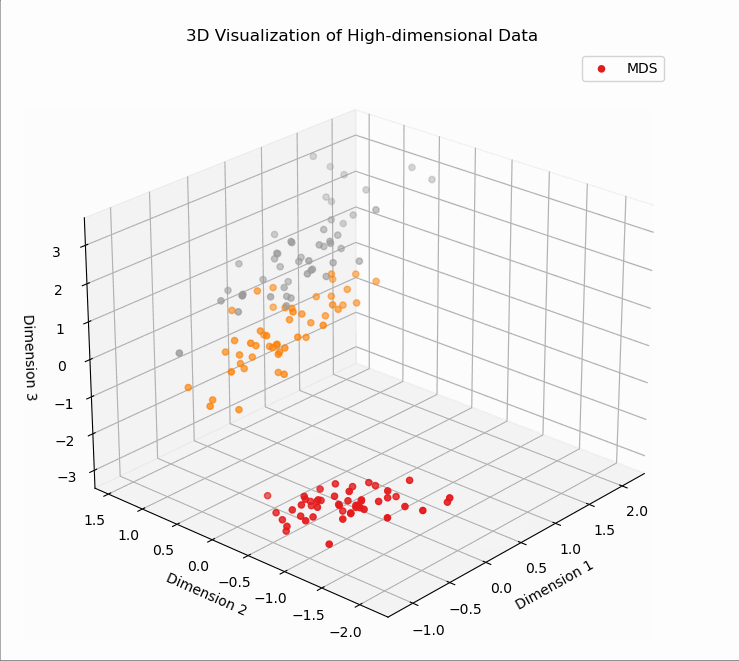
# T4、LDA降维可视化

# T5、T-SNE降维可视化