目录
2.3 因果图与决策表法
2.3.1 因果图设计法
2.3.2 决策表
2.3.3 实例:三角形决策表
2.3.4 实例:工资发放决策表
2.3 因果图与决策表法
等价类划分法与边界值分析法主要侧重于输入条件,却没有考虑这些输入之间的关系,如组合、约束等。
2.3.1 因果图设计法
因果图法是一种利用图解法分析输入的各种组合情况的测试方法,它考虑了输入条件的各种组合及输入条件之间的相互制约关系,并考虑输出情况。
1. 因果图
因果图需要处理输入之间的作用关系,还要考虑输出情况,因此它包含了复杂的逻辑关系,这些复杂的逻辑关系通常用图示来展现,这些图示就是因果图。
因果图使用一些简单的逻辑符号和直线将程序的因(输入)与果(输出)连接起来,一般原因用ci表示,结果用ei表示,ci与ei可以取值“0”或“1”,其中“0”表示状态不出现,“1”表示状态出现。
ci与ei之间有恒等、非(~)、或(∨)、与(∧)4种关系:(下面是因果图)

- 恒等:在恒等关系中,要求程序有1个输入和1个输出,输出与输入保持一致。若c1为1,则e1也为1;若c1为0,则e1也为0。
- 非:非使用符号“~”表示,在这种关系中,要求程序有1个输入和1个输出,输出是输入的取反。若c1为1,则e1为0;若c1为0,则e1为1。
- 或:或使用符号“∨”表示,或关系可以有任意个输入,只要这些输入中有一个为1,则输出为1,否则输出为0。
- 与:与使用符号“∧”表示,与关系也可以有任意个输入,但只有这些输入全部为1,输出才能为1,否则输出为0。
如果程序有多个输入,那么除了输入与输出之间的作用关系之外,这些输入之间往往也会存在某些依赖关系,某些输入条件本身不能同时出现,某一种输入可能会影响其他输入。这些依赖关系在软件测试中称为“约束”,约束的类别可分为4种:E(Exclusive,异)、I(at least one,或)、O(one and only one,唯一)、R(Requires,要求),在因果图中,用特定的符号表明这些约束关系:(下面是多个输入之间的约束符号)
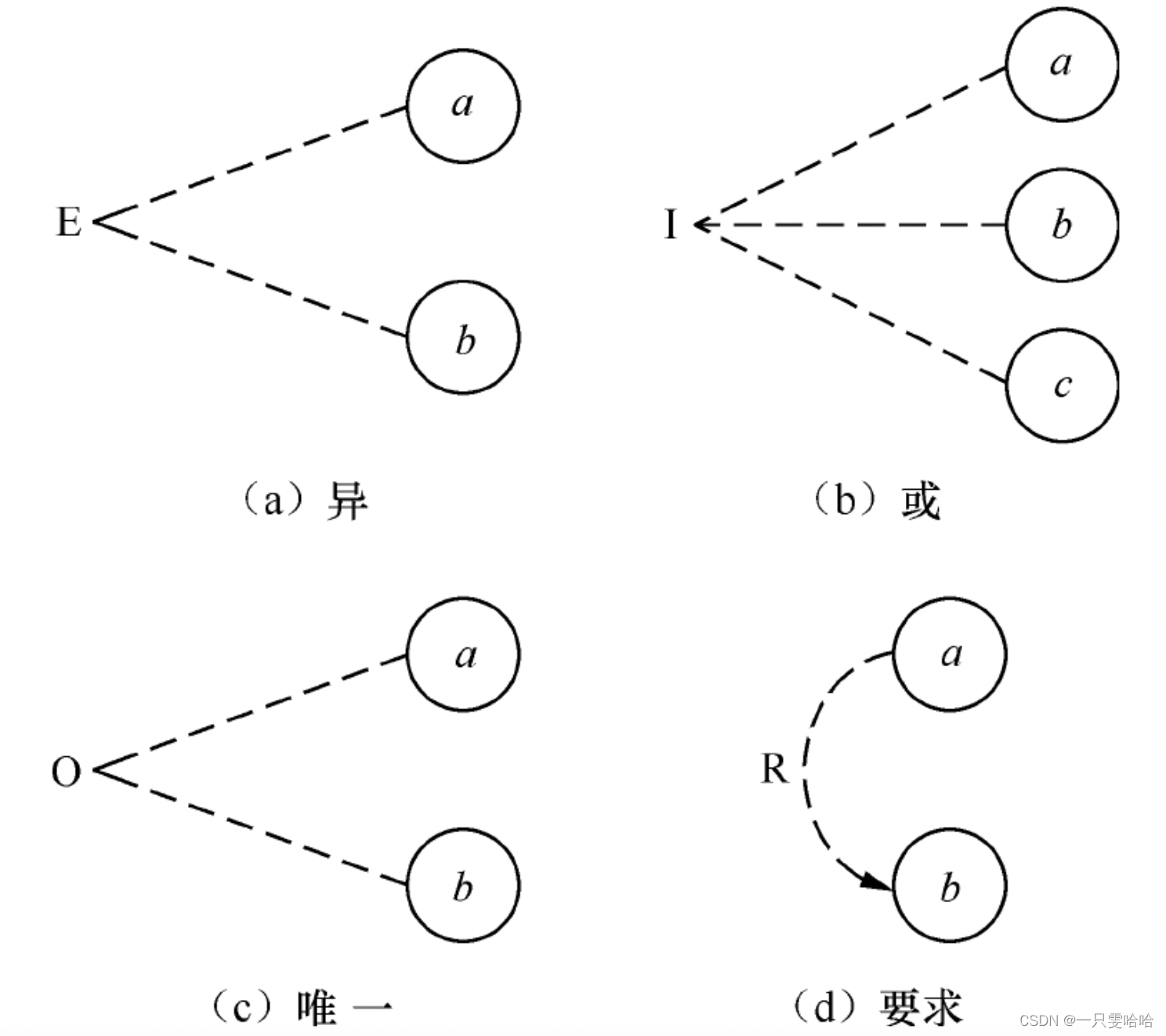
- E(异):a和b中最多只能有一个为1,即a和b不能同时为1。
- I(或):a、b和c中至少有一个必须是1,即a、b、c不能同时为0。
- O(唯一):a和b有且仅有一个为1。
- R(要求):a和b必须保持一致,即a为1时,b也必须为1;a为0时,b也必须为0。
输出条件的约束只有一种——M(Mask,强制):
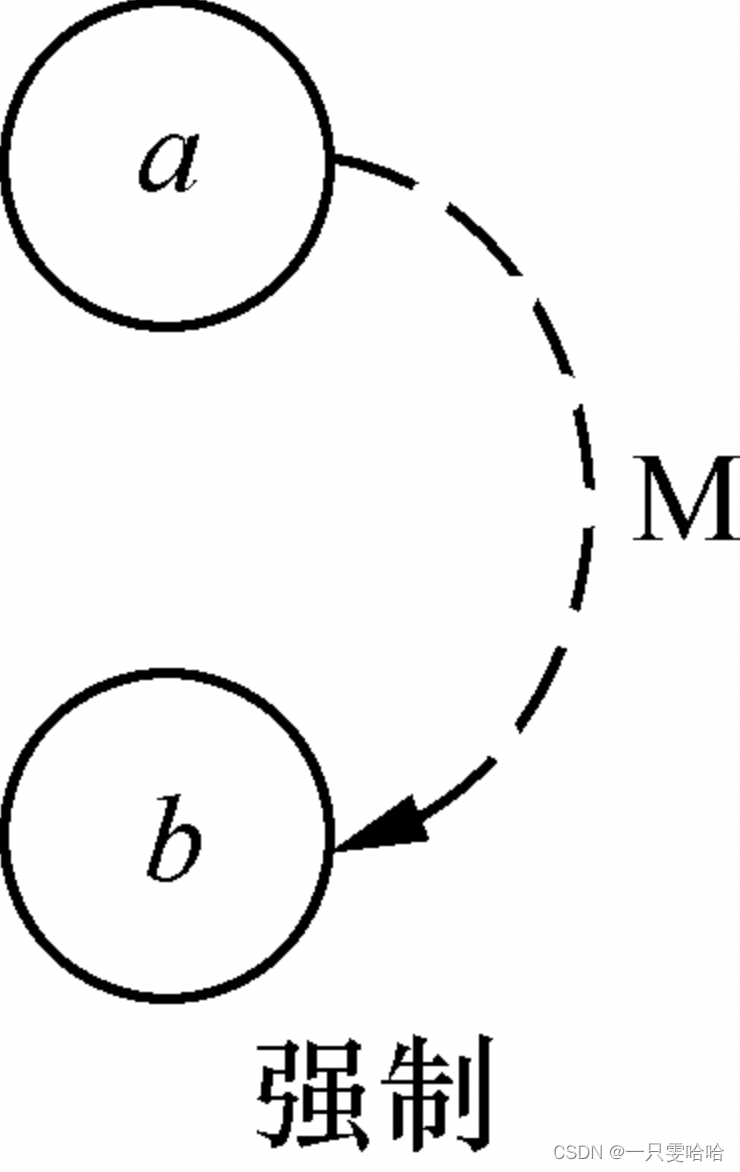
在输出条件的强制约束关系中,如果a为1,则b强制为0;如果a为0,则b强制为1。
2. 因果图法设计测试用例的步骤
(1)分析程序规格说明书描述内容,确定程序的输入与输出,即确定“原因”和“结果”。
(2)分析得出输入与输入之间、输入与输出之间的对应关系,将这些输入与输出之间的关系使用因果图表示出来。
(3)由于语法与环境的限制,有些输入与输入之间、输入与输出之间的组合情况是不可能出现的,对于这种情况,使用符号标记它们之间的限制或约束关系。
(4)将因果图转换为决策表。
(5)根据决策表设计测试用例。
2.3.2 决策表
决策表也称为判定表,其实质就是一种逻辑表。它可以把复杂的逻辑关系和多种条件组合的情况表达得既具体又明确(相比之下,因果图就不够简明),利用决策表可以设计出完整的测试用例集合。
通过一个“图书阅读指南”来制作一个决策表:

根据这个决策表阅读图书,对各种情况的处理一目了然,简洁高效。
决策表通常由4个部分组成:
- 条件桩:列出问题的所有条件,除了某些问题对条件的先后次序有要求之外,通常决策表中所列条件的先后次序都无关紧要。
- 条件项:条件项就是条件桩的所有可能取值。
- 动作桩:动作桩就是问题可能采取的操作,这些操作一般没有先后次序之分。
- 动作项:指出在条件项的各组取值情况下应采取的动作。
这4个组成部分对应到上面的表中:条件桩包括是否疲倦、是否对内容感兴趣、对书中内容是否感到糊涂;条件项包括“Y”与“N”;动作桩包括回到本章开头重读、继续读下去、跳到下一章去读、停止阅读并休息;动作项是指在问题综合情况下所采取的具体动作,动作项与条件项紧密相关,它的值取决于条件项的各组取值情况。
在决策表中,任何一个条件组合的特定取值及其相应要执行的操作称为一条规则,即决策表中的每一列就是一条规则,每一列都可以设计一个测试用例,根据决策表设计测试用例就不会有所遗漏。
将规则进行合并,可以减少重复的规则,相应地减少测试用例的设计,这样可以大大降低软件测试的工作量。

相比于因果图,决策表能够把复杂的问题按各种可能的情况一一列举,简明而易于理解,也避免遗漏,因此在多逻辑条件下执行不同操作的情况,决策表使用得更多。
2.3.3 实例:三角形决策表
这里继续使用三角形讲解决策表的构建与测试用例的设计。三角形的三边是否能构成三角形?如果能构成三角形,那么是构成一般三角形、等腰三角形还是等边三角形?
据此分析,三角形问题有4个原因:是否构成三角形?a=b?b=c?c=a?有5个结果:不构成三角形、一般三角形、等腰三角形、等边三角形、不符合逻辑。
三角形的原因与结果:
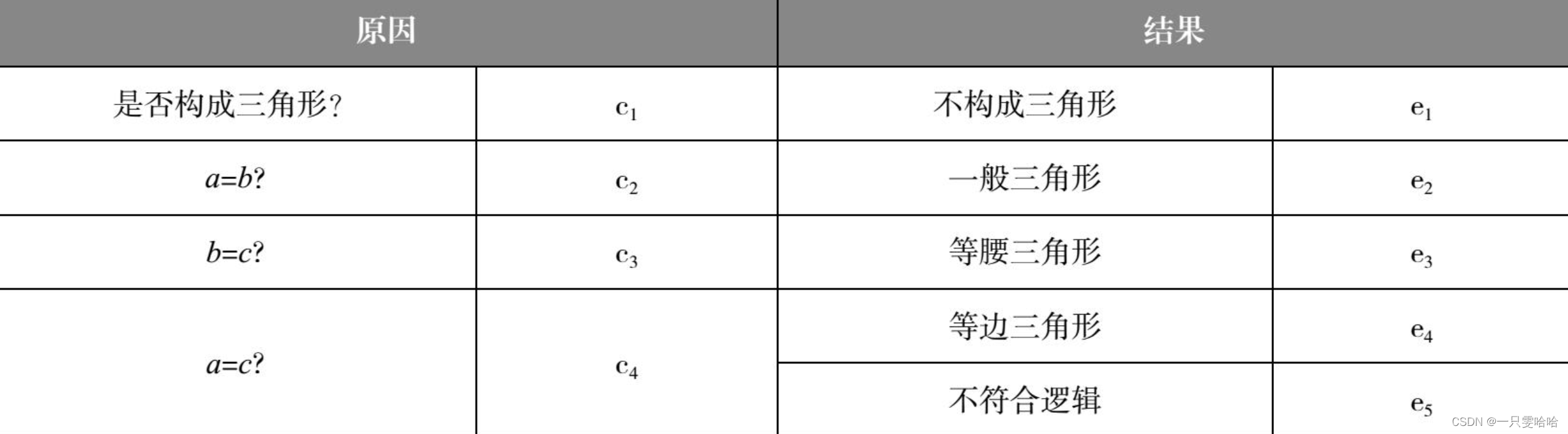
有4个原因,每个原因可取值“Y”和“N”,因此共有2^4=16条规则:

由规则9到规则16可知,只要c1为N,则无论c2、c3、c4取何值结果都是e1,因此c2、c3、c4为无关条件项,可以将规则9到规则16合并成一条规则,而剩余其他规则无法合并简化:

根据上表可设计9个测试用例用于测试三角形:
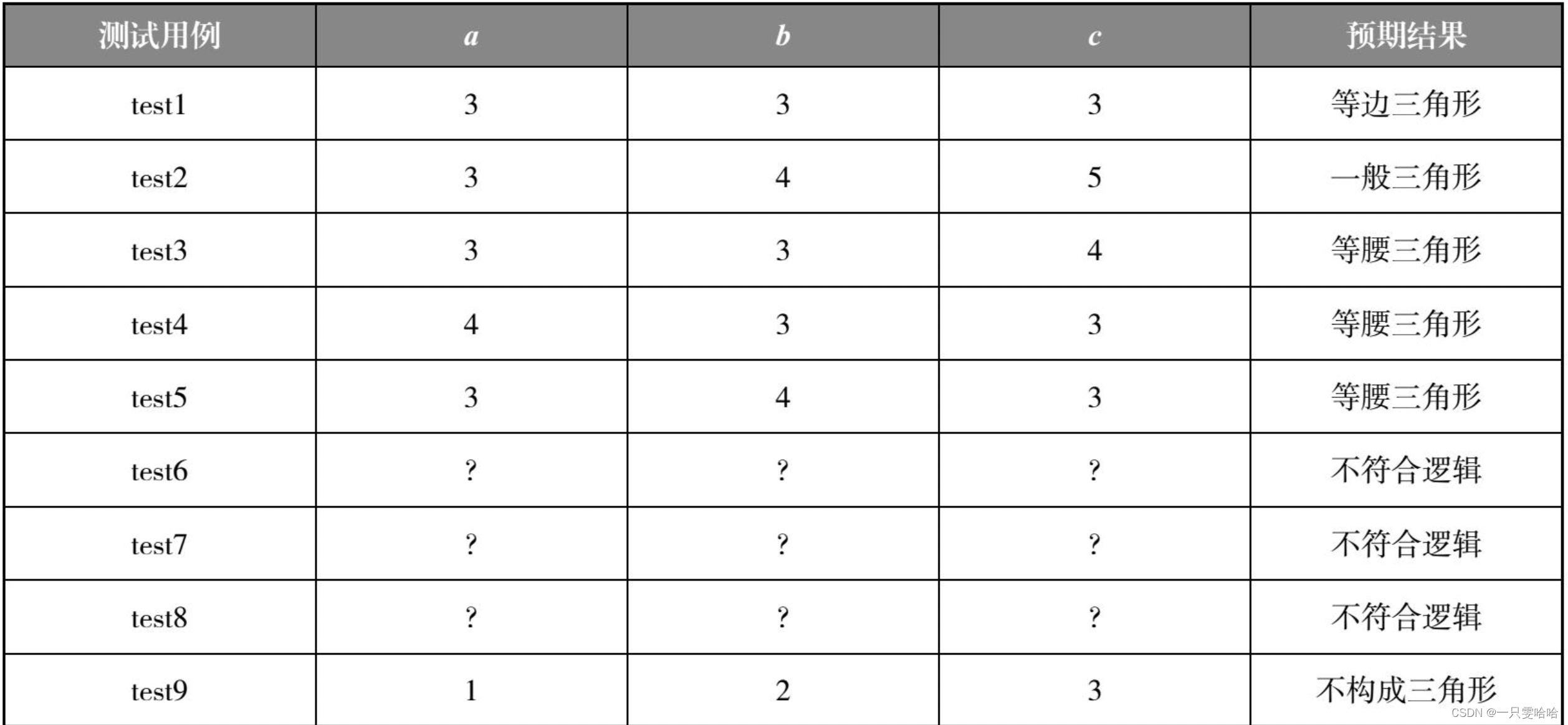
2.3.4 实例:工资发放决策表
某公司的薪资管理制度如下:员工工资分为年薪制与月薪制两种,员工的错误定位包括普通错误与严重错误两种,如果是年薪制的员工,犯普通错误扣款2%,犯严重错误扣款4%;如果是月薪制的员工,犯普通错误扣款4%,犯严重错误扣款8%。
员工工资由4个因素决定:年薪、月薪、普通错误、严重错误,其中年薪与月薪不可能并存,但普通错误与严重错误可以并存;
而员工最终扣款结果有7种:未扣款、扣款2%、扣款4%、扣款6%(2%+4%)、扣款4%、扣款8%、扣款12%(4%+8%)。
员工工资原因与结果:
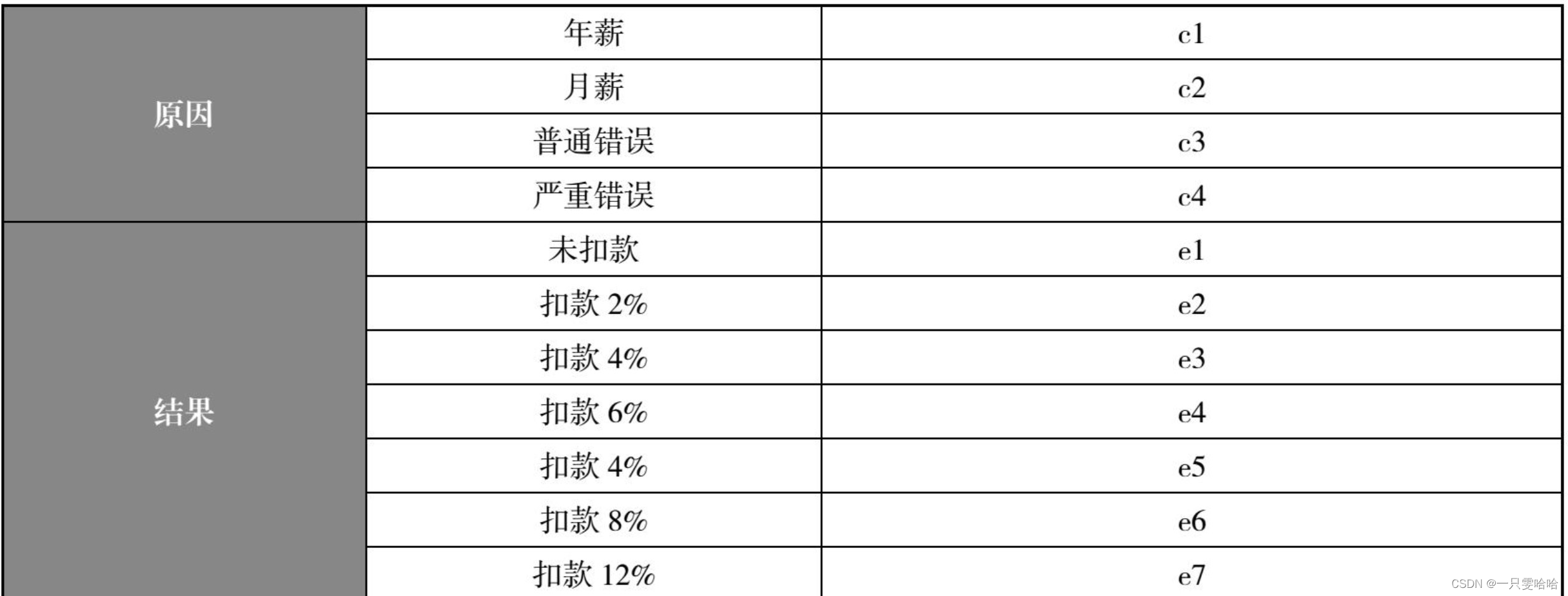
有4个原因,假设每个原因有“Y”和“N”两个取值,理论上可以组成2^4=16种规则,但是c1与c2不能同时并存9(c1确定了,c2随之确定),因此有2^3=8种规则:

分析该员工工资决策表,并没有可以合并的规则,因此在测试时需要设计8个测试用例:

等价类划分和边界值分析法,更适合一些直接的输入数据,彼此之间没有什么逻辑关系的;
而对于一些由多种事件导致不同结果的问题,决策表法更加合适,因为不管输入之间有什么关系, 决策表法都能一一列举出来,覆盖完全,再据此进行测试用例的编写,测试就会更加全面。