怎样评估机器学习算法的性能?
利用机器学习诊断法来评估机器学习算法的性能。诊断法是一种测试法,通过这种测试能够了解算法在哪里出了问题,这也能够告诉我们要想改进一种算法的效果、什么样的尝试才是有意义的。
7.1 评估假设
评价算法学习得到的假设。
怎样判断一个假设是否过拟合呢?
假设我们有这样一组数据组(如图的十组数据),为了确保我们可以评价我们的假设函数,我们将数据分成两部分:第一部分作为训练集,第二部分作为测试集,经典的分割是7:3。但是如果数据集呈现某种规律,那么最好是随机选择训练集和测试集。

以线性回归为例(展示训练和测试学习算法的过程)
- 首先需要对训练集进行学习得到参数
(就是最小化训练误差
)
- 计算出测试误差

如果是分类问题里面的逻辑回归的步骤:
- 首先需要对训练集进行学习得到参数
- 计算测试误差

还可以使用错误分类的方法也叫做0/1分类错误。0和1表示了你预测的分类是正确或错误的情况。
0/1错误分类度量:
把用来测试的数据求出h theta,y,再把两者代入err(h,y)函数中,求出测试数据中的误差,求和后再除以mtest ,就是求测量数据的平均误差。
7.2 模型选择问题
假设想要确定对于一个数据集最合适的多项式次数,怎样选用正确的特征来构造学习算法或者加入需要选择学习算法中的正则化参数lambda,该怎样做呢?——这类问题被叫做模型选择问题。
在这一小节,不是考虑把数据分为训练集和测试集,而是如何将数据分为三个数据组:训练集、验证集和测试集。
如果你的参数对某个数据集拟合的很好,比如说是训练集或者其他数据集,那么用同一数据集计算得到的误差比如训练误差并不能很好地估计出实际的泛化误差,即该假设对新样本的泛化能力。现在,我们来考虑模型选择问题。假设现在要选择能最后地拟合数据的多项式次数,考虑选择一次、二次、...、十次函数中的哪一个?这类似于在这个算法里加入一个参数。这里设置d=1 2 3 4表示一次函数、二次函数、三次函数、四次函数。

如果你想要选择一个模型,就是选择一次多项式次数,从这10个模型中选择一个,拟合这个模型并且估计这个拟合好的模型假设对新样本的泛化能力。那么可以这样做:首先先选择第一个模型,然后最小化训练误差,这样就会得到一个参数向量,然后再选择第二个模型(二次函数)用它来拟合训练集,就会得到另外一个参数向量
,以此类推会得到十个向量参数。取每一个假设和它相应的参数,然后计算出它在测试集的性能。
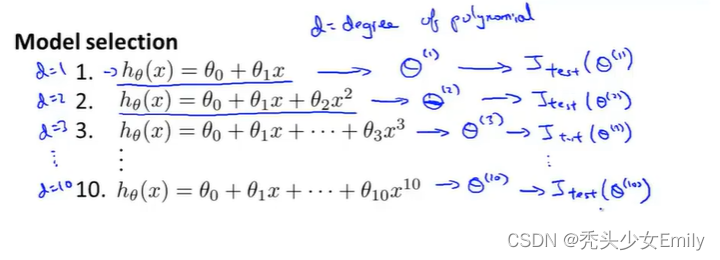
最后选择了五次函数,现在我们想知道这个模型的泛化能力怎么样。我们可以观察这个五次多项式假设模型对测试集的拟合情况,但问题是这样做任然不能公平地估计出这个假设的泛化能力其原因在于我们拟合了一个额外的参数d,也就是多项式的次数。我们用测试集拟合了参数d,我们选择了一个能够最好地拟合测试集的参数d的值。因此我们的参数向量在测试集上的性能很可能是对泛化误差过于乐观的估计。因为使用测试集拟合得到的参数d,再在测试集上评估假设就不公平了。因为我用测试集拟合到的参数用测试集选择了多项式的次数,所以假设很可能对于测试集的表现好过于它没见过的样本,但后者才是我们真正关心的。
如果我们用训练集来拟合参数向量时,拟合后的模型在训练集上的效果是不能预测出假设对于新样本的泛化能力的。这是因为这些参数能够很好地拟合训练集,因此很有可能在训练集上表现地很好,但对其他的新样本来说就不一定那么好了。(也就是训练集和测试集其实还是来自一个数据集中 只不过人为划分出来了70%和30% 所以有可能对这一整个数据集都友好。用测试集来优化训练集的模型,那再用测试集去测试肯定是效果很好;所以我们应该另外取20%的数据作为交叉验证,再用测试集预测效果好不好)
具体来说,我们是在对测试集进行拟合,通过拟合测试得到参数d,这意味着假设在测试集上的效果并不能用来公正的估计这个假设对从未见过的新样本的效果。为了解决模型选择出现的问题,我们通常会采用如下的方法来估计一个假设:
给定一个数据集,不把它分成训练集和测试集,而是分为三个部分:训练集、交叉验证集(cv)、测试集,这些数据典型额分配比例是6:2:2。


当面对这样问题的模型选择,我们需要做的就是:用验证集或者说交叉验证集来选择模型而不是原来的测试集。具体来讲,首先要选取第一种假设,利用最小化函数求出一个参数向量,以此类推。接下来用交叉验证集来测试,然后计算出
来观察这些假设模型在交叉验证集上的效果如何,会选择交叉验证误差最小的那个假设作为我们的模型。

7.3 诊断偏差与方差

训练误差(训练集的平均误差平方和)和验证误差(交叉验证集的平均误差平方和)的定义:
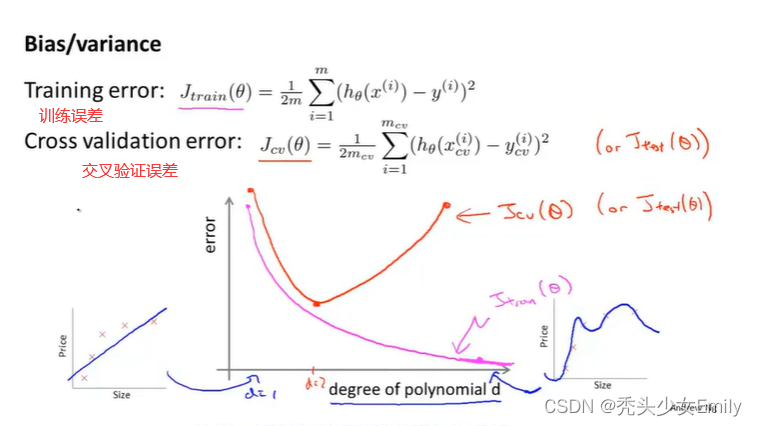
如果交叉验证误差或者训练误差比较大,怎么样判断是高偏差问题还是高方差问题?

训练误差和验证误差都大:欠拟合
训练误差小,验证误差大大:过拟合!
7.4 正则化、偏差和方差

如何自动地选择出一个最合适的正则化参数值

假设在使用正则化的情形中定义训练误差另一种不同的形式,把它定义为最优化目标,去掉正则化项,类似的也可以这样定义交叉验证集误差和测试误差。

选择正则化参数:

得到了这12组模型后,接下来要做的是选用第一个模型,最小化我们的代价函数得到参数向量,以此类推,选择第二个、第三个模型...紧接着,用交叉验证集来评价所得到的参数向量,然后取交叉验证误差最小的模型作为最终选择。

其实思想是差不多的,一个是通过减少维度(数据集),一个是控制theta的相对大小(正则化),核心都是进一步选择效果最好的(泛化性能最佳的)theta。
当改变正则化参数lambda时,交叉验证误差和训练误差怎么变化?
用J(包含正则化项)来求theta,然后为了比较lameda对theta的影响,用Jtrain和Jcv绘制曲线(不包含正则化项)。其实训练时用的是J,而Jtrain和Jcv只是用来画线说明问题。(正则是为了梯度下降的优化,真值的误差本身不包括正则,所以训练误差没有正则)
把数据分成训练集+验证集+测试集后,就是拿带有正则化的去拟合参数,这里的J_train指的是你训练出来的预测值和真实值的误差!

lambda大,就把一些相关性不大的特征的theta变为0了,就修正了过拟合的问题,而且这是针对训练集,所以再用不带正则化的代价函数去测试训练集偏差就大了,lambda小,就过拟合了。
7.5 学习曲线
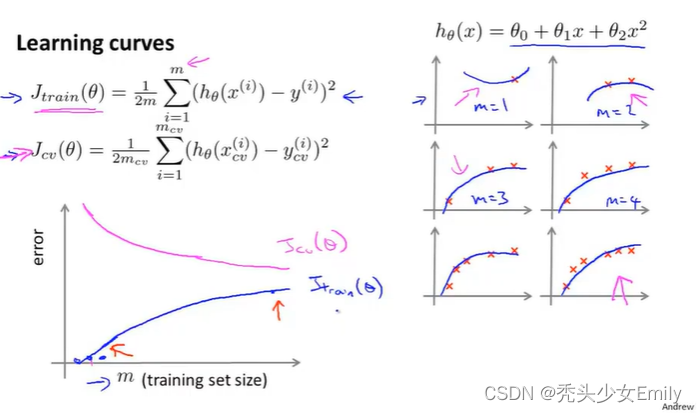 假设你的假设出现高偏差问题
假设你的假设出现高偏差问题

偏差大对应欠拟合,欠拟合可以理解为模型简单,未捕捉到数据集的特征(高偏差(欠拟合)添加数据无效)。
如果一个学习算法有高偏差,随着我们增加训练样本就是向着上图的横坐标右边移动,发现交叉验证误差不会明显下降了,基本变成平的了。所以如果学习算法正处于高偏差的情形,那么选用更多的训练集数据对于改善算法表现无益。
当学习算法出现高方差问题时,如果你的训练集很小,我们的训练误差会很小。随着训练集样本容量的增加,可能仍然会有些过拟合,但此时要对数据很好地拟合变得更加困难。

这个曲线图也反映出,如果我们考虑增大训练集的样本数,就是上图横坐标向右延伸的曲线。
过拟合说的是模拟于训练数据集,拟合程度很高并且复杂程度也很高。过拟合,一般就是训练集error很低,但是验证集的error降不下来。
高偏差是欠拟合,高方差是过拟合(参数少:欠拟合,参数多:过拟合)。
学习曲线有利于我们弄清哪些方法有助于改进学习算法的效果。
我们试图用正则化的线性回归拟合模型发现并没有达到我们预期的效果,我们有了如下很多选择,哪些方法有效呢?

feature的数量应与m相匹配,feature过少或m过大时表现为欠拟合,feature过少或m过小时表现为过拟合,所以欠拟合是增加feature没有问题。拉姆达负责修正,提高拉姆达是为了解决过拟合。
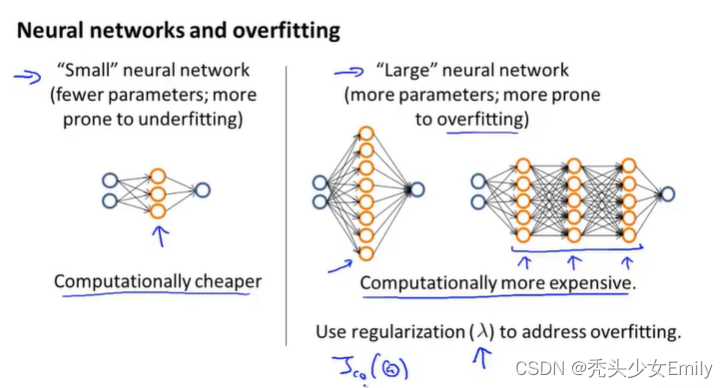
交叉验证误差或者测试误差是检验模型对新样本泛化能力,能不能对新样本做出好的预测。