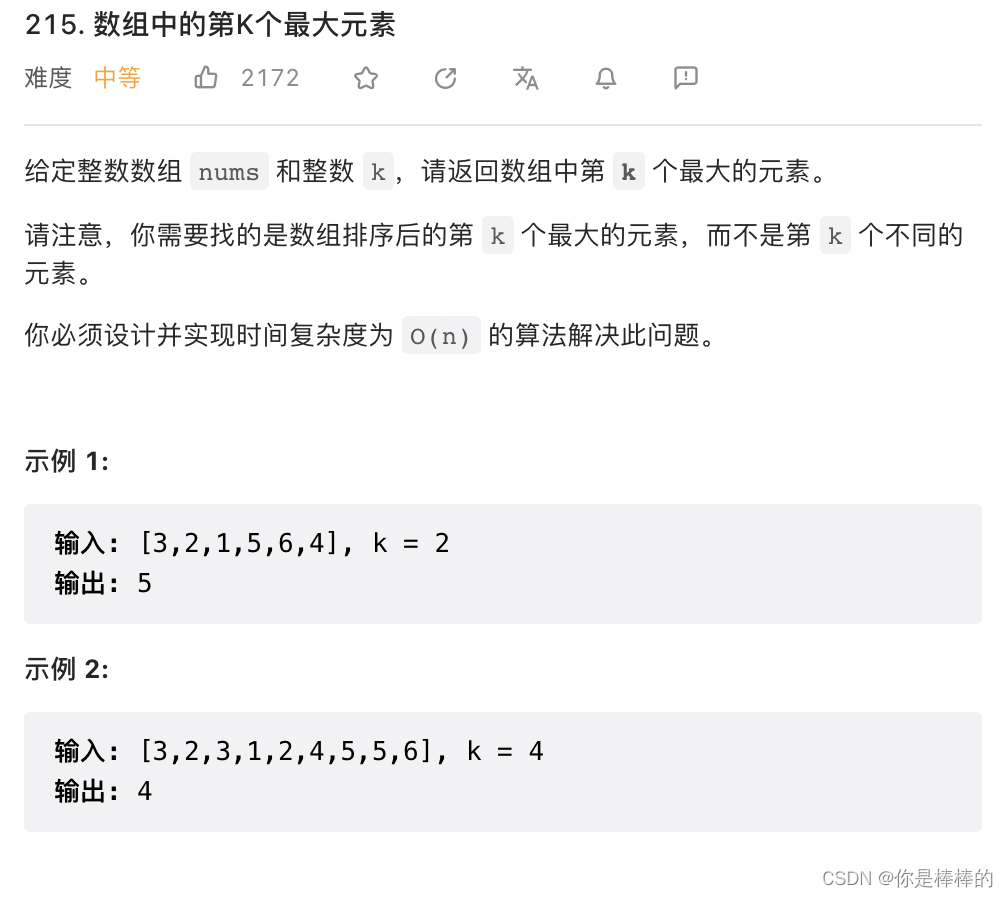
解题思路：

利用快排的思想，不断地将数组分成若干部分，缩小查找范围，最终找到第 k 大的元素。

1、首先，对数组进行快速排序，使得数组从大到小排序，然后返回排序后的第 k 个元素即可。

2、在快排过程中，我们每次都选择一个基准数，将数组分为两部分，左部分的数都比基准数大，右部分的数都比基准数小。

3、若基准数所在的位置大于 k，说明需要在基准数左侧的区间中寻找第 k 大的数，此时再对左侧区间进行快排；

4、若基准数所在的位置小于 k，说明需要在基准数右侧的区间中寻找第 k 大的数，此时再对右侧区间进行快排。

5、在快排分区过程中，我们随机从待排区间选取一个数作为基准数，这是为了避免在特定情况下时间复杂度退化为 O(n^2)。同时，我们也要注意处理数组下标的边界情况。

时间复杂度：O(n )

1、对 nums 进行快排，快排的时间复杂度为 O(nlog⁡n)

2、在快排过程中，我们只对基于基准数的一侧继续进行递归，因此时间复杂度是线性的，即 O(n)。

空间复杂度：O((logn )

快排递归过程中使用的栈空间决定的，在栈中，而快排的递归深度是 O(log⁡n)。

//215.数组的第k大元素
func findKthLargest(nums []int,k int)int{//定义查找第k大元素的函数
	quickPartition(nums,0,len(nums)-1,k-1) // 对待排数组进行快排分区
	return nums[k-1]//返回排序后的第k大元素
}
//定义快排分区函数，输入参数为待排序数组，待排区间的左右边界和目标位置
func quickPartition(nums []int,left,right,target int){
	rand.Seed(time.Now().UnixNano())//以当前时间为种子生成随机数
	random:=rand.Int()%(right-left+1) +left//生成在待排区间内的随机数//如果rand.Int()返回的随机整数为33，则rand.Int()%(9)的结果就是33%9=6。
    // random:=rand.Intn(right-left+1) +left
	privot:=nums[random]//以随机数为下标，用该随机数下标获得的元素作为基准数
	nums[left],nums[random]=nums[random],nums[left]//将待排区间的第一个元素与基准数交换位置
	index:=left//初始化index为待排区间左端点

	for i:=left+1;i<=right;i++{//从待排区间的第二个元素开始，依次与基准数比较大小，将比基准数大的元素放到待排区间的前面
		if nums[i]>=privot{
			index++
			//比基数大的放在左边，比基数小保留在已排序的元素序列的右侧，等待下一轮与更大的元素交换位置。
			nums[index],nums[i]=nums[i],nums[index]
		}
	}
	//最后，循环结束时，已经把比基数大的元素放在左边，比基数小的元素放在右边。
	//这时候要把基数放在正确的位置，基数是左边大元素中的最小值，要把基数放在这些大元素的末尾，
	//即要跟排好的最后一个大元素nums[index]交换位置
	//这时候我们不用管基数左右两边的数是否排好序，因为基数左边的数都是比他大的，右边的都是比他小的，
	//所以index位置的基数就是左边大元素的最小数，可以判断出它现在处于数组的第几个最大元素
	nums[index],nums[left]=nums[left],nums[index]
	//然后再去判断是不是我们要的第k大，如果当前index比第k大的数还小，那么第k大在index的左边，继续在基数左边的数组里分区
	//如果当前index比第k大的数还大，那么第k大在index的右边，继续在基数右边的数组里分区

     if index<target{
		quickPartition(nums,index+1,right,target)
	}else if index>target {
		quickPartition(nums,left,index-1,target)
	}
}