🌈目录

1. 排序的概念
2. 常见的排序算法
3. 排序算法的实现
- 3.1 插入排序
- - 3.1.1 直接插入排序
  - 3.1.2 希尔排序（缩小增量排序）
- 3.2 选择排序
- - 3.2.1 基本思想
  - 3.2.2 直接选择排序
  - 3.2.3 堆排序

1. 排序的概念

排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性：假设在待排序的序列中，存在多个具有相同内容的元素，如果经过排序，这些元素的相对位置并不发生改变，则称这种排序算法是稳定的。

稳定的排序可以变成不稳定的，但是不稳定的排序算法是不可能变成稳定的。

例如：

排序前：4_a 6 5 9 3 4_b 7 2

排序后：2 3 4_a 4_b 5 6 7 9 ==》稳定

排序后：2 3 4_b 4_a 5 6 7 9 ==》不稳定

稳定性存在的意义是什么？

比如说：小明用半小时交卷得了一百分，小刚用一小时交卷得了一百分，最终以分数排名的时候，第一名一定是小明，不可能是小刚，因为小明比小刚先交卷。

稳定性好的排序就会把小明放在第一名，而稳定性差的排序可能会把小刚放在第一名，对小明不公平。

这样稳定性的意义就体现出来了。

内部排序：数据元素全部放在内存中的排序。

外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求在内外存之间移动数据的排序。

2. 常见的排序算法

在这里插入图片描述

3. 排序算法的实现

3.1 插入排序

插入排序的中心思想就是：将待排序的元素按照自身大小逐个插入到已经排好序的有序序列中，直到所有的元素插完为止。

3.1.1 直接插入排序

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移。

public static void insertSort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int n = array[i];//当前待排序元素
        int j = i - 1;
        for (; j >= 0; j--) {
            //待排序的元素与前面排好序的元素进行比较
            if(n < array[j]) {
                //当前待排序元素<排好序的元素
                array[j + 1] = array[j];
                //排好序的元素后移
            } else {
                //当前待排序元素>=排好序的元素，证明此时待排序元素找到了自己的位置，中断比较
                break;
            }
        }
        array[j + 1] = n;//将待排序的元素放在自己的位置。
        //为什么是将待排序的元素赋值给array[j + 1]呢？
        //因为array[j + 1] > n > array[j] ,array[j + 1] 的值已经赋给后一个元素了，所以将待排序的元素赋值给array[j + 1]
    }
}

测试10_0000个数据排序所用时间（单位：ms）

在这里插入图片描述

特点：

元素集合越接近有序，直接插入排序算法的时间效率越高。
时间复杂度：最坏的情况下（逆序）O(N²)，最好的情况下（正序）O(N);
数据越有序的时候，排序越快
空间复杂度：O(1)
稳定性：稳定

3.1.2 希尔排序（缩小增量排序）

希尔排序的中心思想是：

先选定一个整数，把待排序元素分成多个组，将所有距离为n的元素分到一组内，然后对每一组内的元素进行排序，然后取n的一半或者其他小于n的整数，重复上述工作。当n = 1时，所有的元素在统一组内排好序。

简单来说，就分为两步：

分组->缩小增量

这里的分组并不是将连续的元素分在一组内，而是跳跃式分组，这样可以尽量把大的数据放到后面，把小的数据放到前面
组内进行插入排序

组内的每一次排序都是插入排序

gap的取法有很多种：可以是gap = n / 2，gap = gap / 2；也可以是gap = gap / 3 + 1；还有人说都取奇数为好；也有人提出gap互质为好。但是无论哪一种都没有得到证明。

我用的是gap = n / 2，gap = gap / 2这种取法。

下面是大体步骤：

在这里插入图片描述

public static void shell(int[] arr, int gap) {
    for(int i = gap; i < arr.length; i++) {
        //这里为什么是i++而不是i+=gap的原因：
        //因为如果是i+=gap，i只会比较第一个组，因为第一个组比较完了之后，i > arr.length，不能进入循环了。
        //而如果是i++，那么i就会遍历到每一个组，每一个成员，进行插入排序。
        int n = arr[i];
        int j = i - gap;
        for(; j >= 0; j-=gap) {
            //这里j-=gap就能保证每个元素都在自己的组内进行比较
            if(arr[j] > n) {
                arr[j + gap] = arr[j];
            } else {
                break;
            }
        }
        arr[j + gap] = n;
    }
}
public static void shellSort(int[] arr) {
    int gap = arr.length;
    while(gap > 1) {
        gap /= 2;
        shell(arr, gap);
    }
}

在这里插入图片描述

特点

希尔排序是对直接插入排序的优化
当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近于有序了，这样就会很快。
希尔排序的时间复杂度不好计算，因为他的运行时间依赖于gap的选择，导致很难去计算，是一个长期未解决的问题。在很多书中给出的时间复杂度都不固定。大约是在n^1.25 到1.6*n^1.25 范围内
不稳定

3.2 选择排序

3.2.1 基本思想

每一次从待排序的数据元素中选出最小（大）的一个元素，存放在序列的起始位置，直到全部待排序的元素排完。

3.2.2 直接选择排序

升序：在元素arr[i] – arr[n - 1]中选出最小的元素，与arr[i]进行交换，i++，重复上述步骤，直到i遍历到最后一个元素为止。

public static void selectSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        int index = i;
        for (int j = i + 1; j < arr.length; j++) {
            if(arr[index] > arr[j]) {
                //挑选最小元素，记录位置
                index = j;
            }
        }
        swap(arr, i, index);
    }
}
private static void swap(int[] arr, int index1, int index2) {
    int n = arr[index1];
    arr[index1] = arr[index2];
    arr[index2] = n;
}

还有另一种做法，就是每次遍历都会找出一个最大值和最小值，进行两次交换。两种做法的时间复杂度是一样的。

public static void selectSort0(int[] arr) {
    int left = 0;
    int right = arr.length - 1;
    while (right > left) {
        int minIndex = left;
        int maxIndex = left;
        for(int i = left + 1; i <= right; i++) {
            if(arr[i] < arr[minIndex]) {
                minIndex = i;
            }
            if (arr[i] > arr[maxIndex]) {
                maxIndex = i;
            }
        }
        swap(arr, minIndex, left);
        //这里要特别注意一点：
        //如果left这个下标的值是最大值，left和minIndex换了之后，最大值的下标就不是maxIndex了，最大值就被换到了minIndex了，所以这里要判断一下。
        if(maxIndex == left) {
            maxIndex = minIndex;
        }
        swap(arr, maxIndex, right);

        left++;
        right--;
    }
}

特点:

直接选择排序的思路好理解，但是效率比较低，不常用
时间复杂度：O(N²)，数组本身的序列对选择排序的时间复杂度没有影响。
空间复杂度：O(1)
不稳定

在这里插入图片描述

可能会有人奇怪，逆序情况下，直接插入排序和选择排序的时间复杂度都是O(N²)，为什么时间相差很多呢？

因为插入排序越排序越有序，越有序就越快。

注意：这里展现的时间只是感受一下排序之间的不同，仅供参考，每次运行的结果都不一样，并且数据量比较小，不能说明排序的时间复杂度！

3.2.3 堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

建堆

升序：建大堆
降序：建小堆

利用堆删除思想来进行排序
按升序来举例，升序要建大堆，为什么呢？因为大根堆可以保证堆顶元素是最大的，然后可以将堆顶元素和最后一个元素进行交换，这样就能确保最大的元素在最后面，然后再对0下标这棵树向下调整，以此类推，就可以得到一组有序的数据。
如图所示：

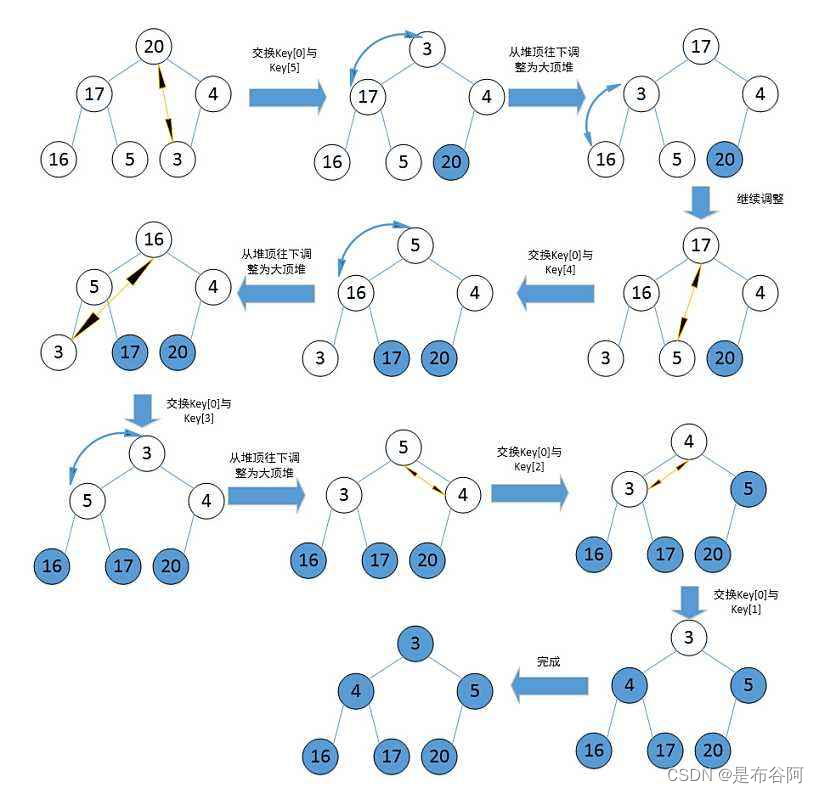
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

public static void heapSort(int[] arr) {
    createBigHeat(arr);
    int end = arr.length - 1;
    while (end > 0) {
        //让堆顶元素与最后一个元素进行交换，因为堆顶元素是最大的元素，将它放在最后一个，就让最大的元素有序了
        swap(arr, 0, end);
        //只有0下标这棵树不符合大根堆，所以只需对0下标这一颗树进行向下调整就行
        siftDown(arr, 0, end);
        end--;
    }
}
private static void createBigHeat(int[] arr) {
    for (int i = (arr.length - 1 - 1) / 2; i >= 0; i--) {
        siftDown(arr, i, arr.length);
    }
}
private static void siftDown(int[] arr, int parent, int len) {
    int child = parent * 2 + 1;
    while(child < len) {
        if(child + 1 < len && arr[child] < arr[child + 1]) {
            child++;
        }
        if(arr[child] > arr[parent]) {
            swap(arr, child, parent);
            parent = child;
            child = parent * 2 + 1;
        } else {
            break;
        }
    }
}