作业名:C2_W4_lecture.ipynb
作业地址:
github --> bharathikannann/AI-for-Medicine-Specialization-deeplearning.ai --> AI for Medical Prognosis --> Week 4
One-hot encode categorical variables
首先我们来看一下哪些特征是分类特征?
import pandas as pd
df = pd.DataFrame({'ascites': [0,1,0,1],
'edema': [0.5,0,1,0.5],
'stage': [3,4,3,4],
'cholesterol': [200.5,180.2,190.5,210.3]
})
df
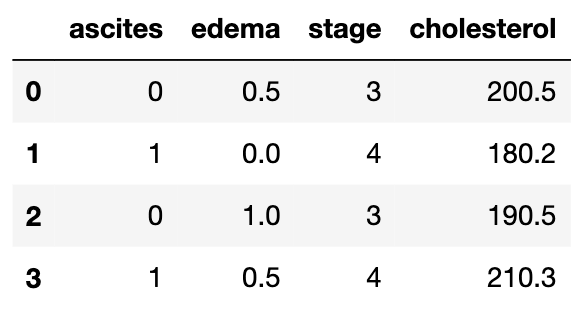
在这个小样本数据集中,“腹水”、“水肿”和“分期”是分类变量
- 腹水(ascites): 取值为0或1
- 水肿(edema):值为0、0.5或1
- 阶段(stage):是3或4
“胆固醇”(cholesterol)是一个连续变量,因为它可以是大于零的任何十进制值。
哪些分类变量要进行one-hot编码?
在分类变量中,哪一个应该进行 one-hot 编码(变成虚拟变量)?
- 腹水:已经是0或1,所以没有必要进行 one-hot 编码。
- 我们可以对腹水进行 one-hot 编码,但当只有两个可能的值是0或1时,就没有必要了
- 当值为0或1时,1意味着存在疾病,而0意味着正常(无疾病)。
- 水肿: 水肿是指身体任何部位的肿胀。这个数据集的 "水肿 "特征有3个类别,所以我们要对它进行one-hot编码,使三个可能的值都有一个特征列。
- 0:无水肿
- 0.5:患者有水肿,但没有接受利尿剂治疗(用于治疗水肿)
- 1:患者有水肿,接受了利尿剂治疗(所以病情可能更严重)。
- 阶段:有3和4的值。我们要对这些进行one-hot编码,因为它们不是0或1的值。
- 癌症的 "阶段 "是0、1、2、3或4。
- 0期意味着没有癌症。
- 第1阶段是仅限于身体的一个小区域的癌症,也被称为 “早期癌症”
- 第2阶段是已经扩散到附近组织的癌症
- 第3阶段是已经扩散到附近组织的癌症,但比第2阶段更严重
- 第4阶段是已经扩散到身体远处的癌症,也被称为 “转移性癌症”。
- 为了训练模型,我们可以将第3阶段转换成0,第4阶段转换成1。这可能会让审查我们代码和数据的人感到困惑。我们将对 "阶段 "进行one-hot。-实际上你会看到,我们最终用0代表第3阶段,1代表第4阶段(见下一节)。
one-hot 特征的多重共线性
让我们看看当我们对“阶段”特征进行one-hot编码时会发生什么?
df_stage = pd.get_dummies(data=df,
columns=['stage']
)
df_stage[['stage_3','stage_4']]
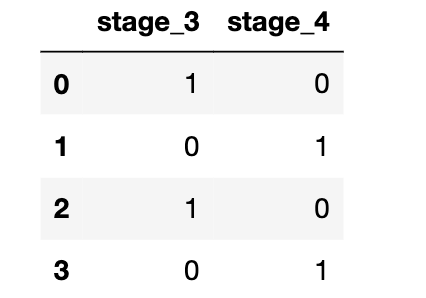
你注意到“stage_3”和“stage_4”特征有什么不同?
考虑到stage只有stage_3和stage_4这两个可能的值,
如果你知道病人0(第0行)的stage_3的值为1,那么你可以说些什么关于该病人的stage_4特征的值?
- 当stage_3为1时,stage_4必须为0;
- 当stage_3为0时,stage_4必须为1。
这意味着其中一个特征列实际上是多余的。我们应该删除这些特征中的一个,以避免多重共线性(其中一个特征可以预测另一个特征)。
可以使用下面方法
df_stage_drop_first = df_stage.drop(columns='stage_3')
也可以直接在刚才的地方添加新的参数drop_first
df_stage = pd.get_dummies(data=df,
columns=['stage'], drop_first=True,
)
df_stage
pd.get_dummies函数有多个参数,下面列举其中几个常用的参数:
- data:要进行编码的DataFrame或Series对象;
- columns:指定要编码的列名,可以是单个列名或列名列表;
- prefix:为生成的哑变量列添加指定的前缀;
- prefix_sep:用于在前缀和列名之间添加分隔符的字符串;
- dummy_na:指定是否在生成的哑变量中包含缺失值,默认为False;
- drop_first:指定是否删除生成哑变量的第一列,以避免多重共线性,默认为False;
- dtype:生成的哑变量的数据类型。
这些参数可以根据需要进行设置,以满足不同的数据分析和机器学习任务的需求。
Hazard function
风险函数的公式为:
λ
(
t
,
x
)
=
λ
0
(
t
)
e
θ
T
X
i
\lambda(t, x) = \lambda_0(t)e^{\theta^T X_i}
λ(t,x)=λ0(t)eθTXi
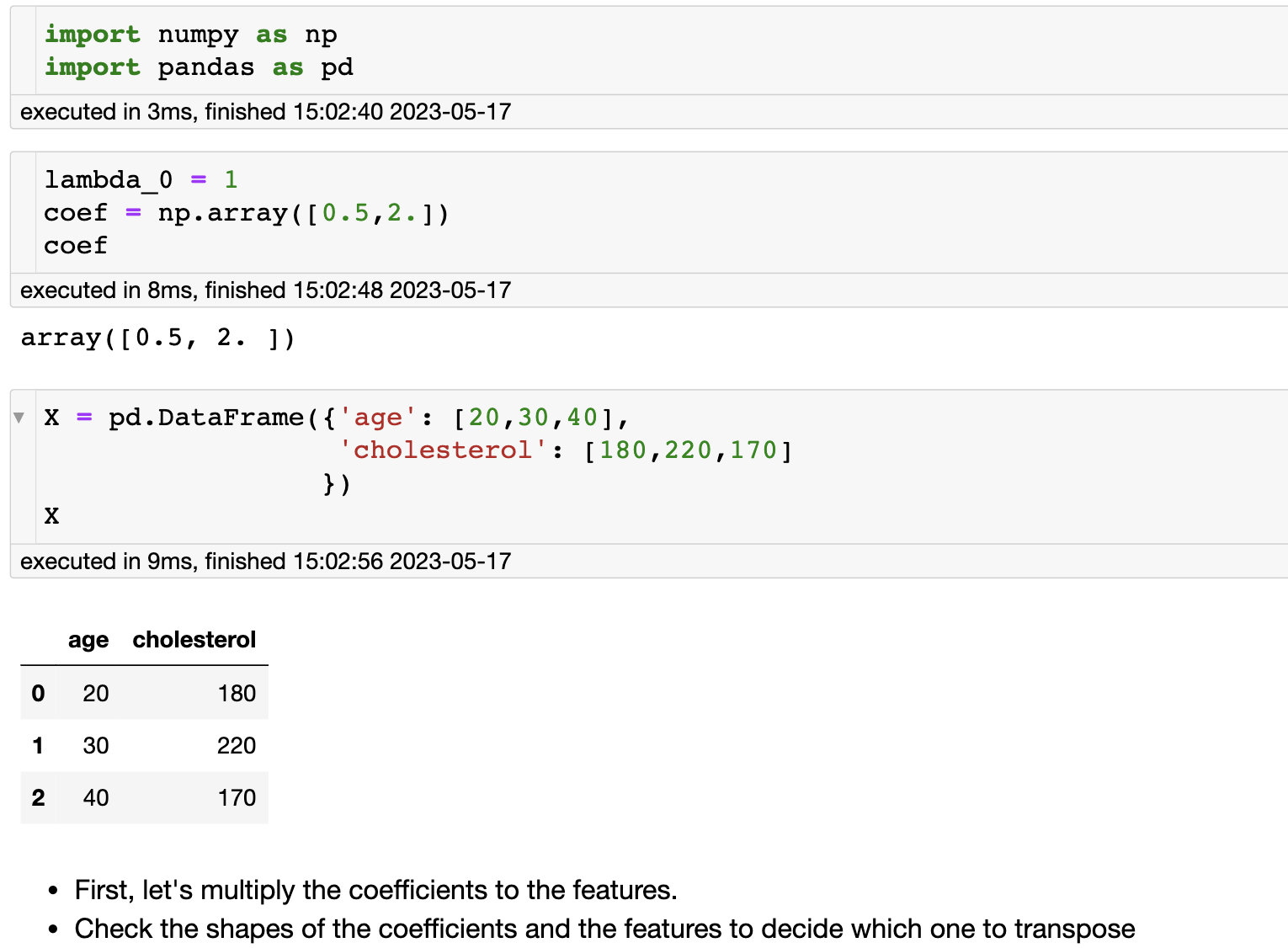
这样我们就有了变量
X
i
X_i
Xi中的特征的系数
θ
\theta
θ。
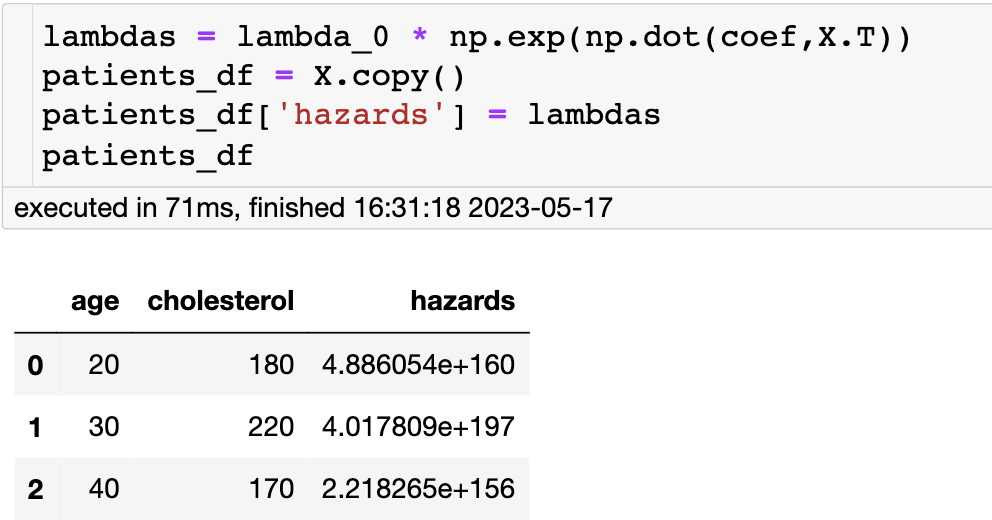
如果你有一个新的病人,我们可以预测他们的风险函数
λ
(
t
,
x
)
\lambda(t,x)
λ(t,x)。

文章持续更新,可以关注微信公众号【医学图像人工智能实战营】获取最新动态,一个关注于医学图像处理领域前沿科技的公众号。坚持已实践为主,手把手带你做项目,打比赛,写论文。凡原创文章皆提供理论讲解,实验代码,实验数据。只有实践才能成长的更快,关注我们,一起学习进步~
我是Tina, 我们下篇博客见~
白天工作晚上写文,呕心沥血
觉得写的不错的话最后,求点赞,评论,收藏。或者一键三连