目录
写在前面:
题目:821. 跳台阶 - AcWing题库
题目描述:
输入格式:
输出格式:
数据范围:
输入样例:
输出样例:
解题思路:
方法一:暴力搜索
代码
方法二:记忆化搜索
代码
方法三:动态规划
代码
AC !!!!!!!!!!
写在最后:
写在前面:
怎么样才能学好一个算法?
我个人认为,系统性的刷题尤为重要,
所以,为了学好动态规划,应对 “DP杯”。
事不宜迟,我们即刻开始刷题!
题目:821. 跳台阶 - AcWing题库
题目描述:
一个楼梯共有 n 级台阶,每次可以走一级或者两级,
问从第 0 级台阶走到第 n 级台阶一共有多少种方案。
输入格式:
共一行,包含一个整数 n。
输出格式:
共一行,包含一个整数,表示方案数。
数据范围:
1 ≤ n ≤ 15
输入样例:
5输出样例:
8解题思路:
这道题是一道经典的dp入门题目,
我打算使用三种方法去做,层层推进,一起入门递归:
方法一:暴力搜索
这道题在之前dfs的刷题中也有出现,
我们可以用dfs搜索所有的方案:
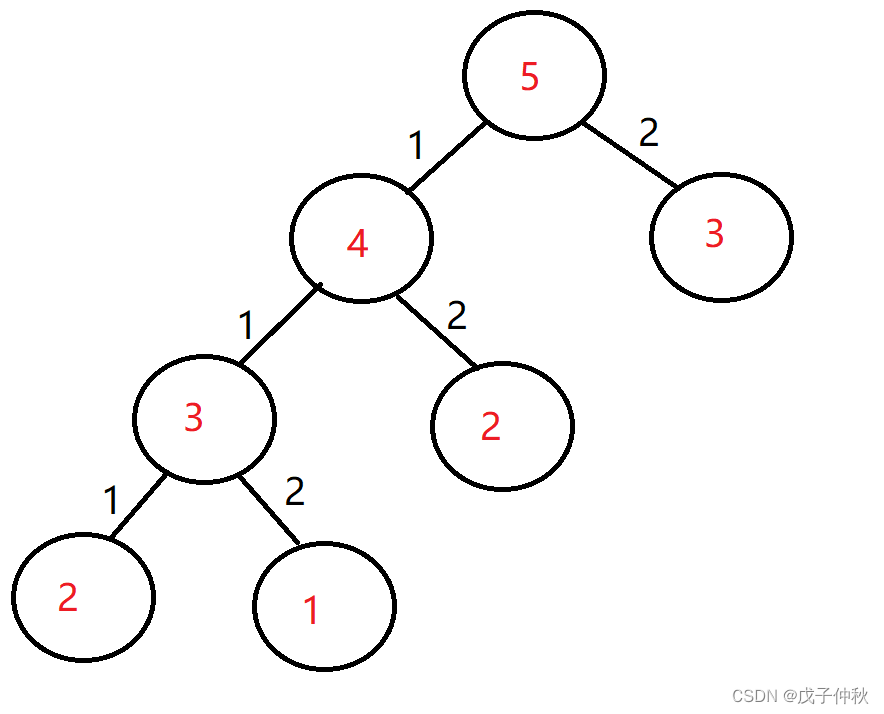
跳三级台阶就是跳两级台阶的方法+跳一级台阶的方法;
跳四级台阶就是跳三级台阶的方法+跳二级台阶的方法;
以此类推:
最后得出答案:
代码如下:
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int n = 0;
int dfs(int u)
{
if(u == 1) return 1;
else if(u == 2) return 2;
return dfs(u - 1) + dfs(u - 2);
}
int main()
{
scanf("%d", &n);
int res = dfs(n);
printf("%d", res);
return 0;
}
方法二:记忆化搜索
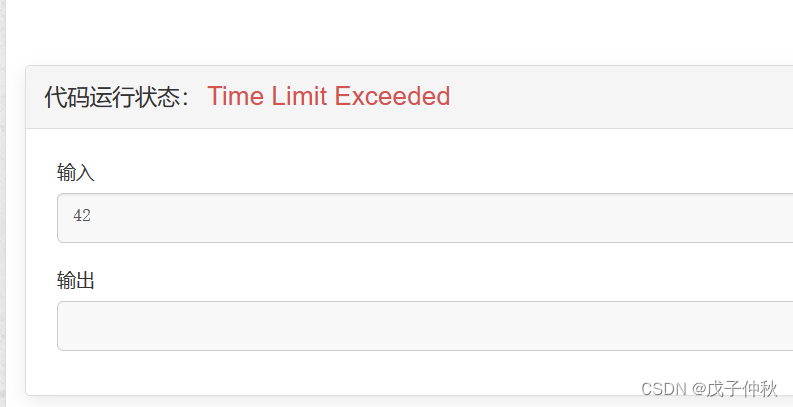
实际上第一种方法的时间复杂度太高,
有2的n次方那么大:
如果n >= 42,就会超时:
为了减少时间的消耗,我们可以用记忆化搜索:
将已经求过的值记录到一个数组中,
这样搜索过的值就不用重复搜索:
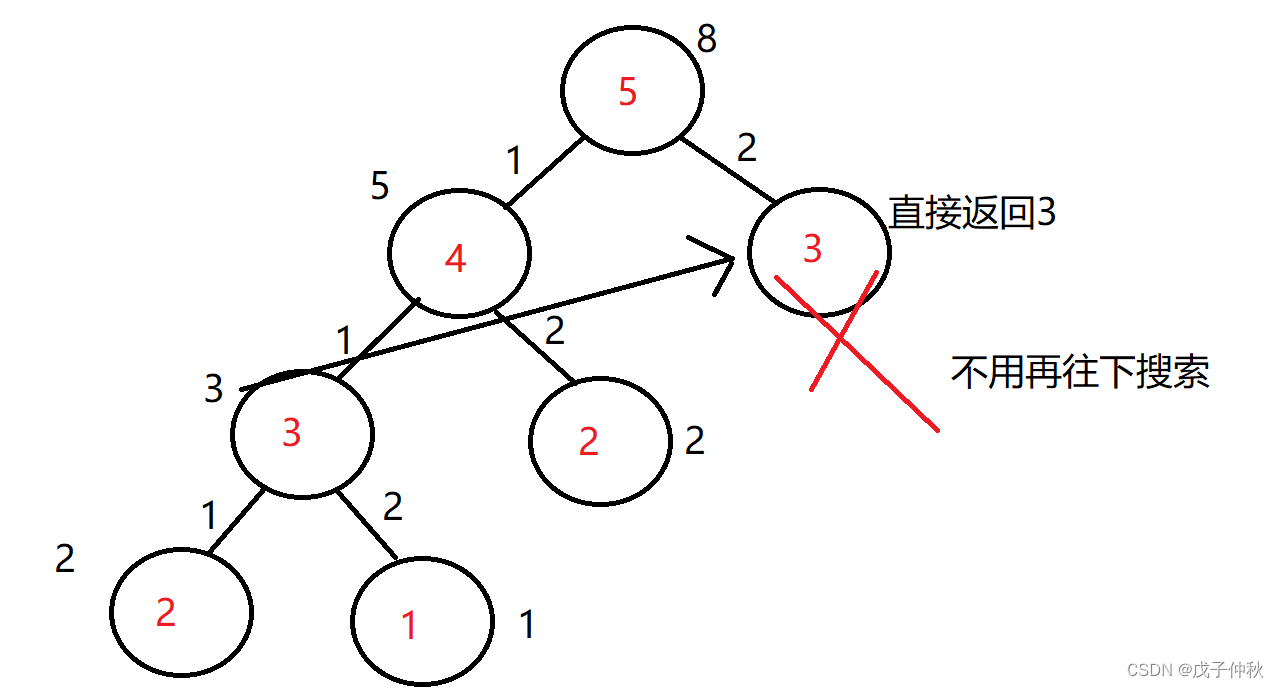
下面是代码实现:
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int n = 0;
int sum = 0;
const int N = 30;
int mem[N];//用一个数组记录
int dfs(int u)
{
if(mem[u]) return mem[u];//如果记录过,就不用往下搜索了
if(u == 1) return 1;
else if(u == 2) return 2;
else sum = dfs(u - 1) + dfs(u - 2);
mem[u] = sum;//将该位置的值记录进数组
return mem[u];
}
int main()
{
scanf("%d", &n);
int res = dfs(n);
printf("%d", res);
return 0;
}
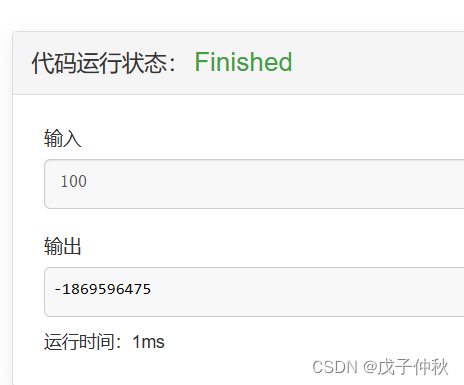
我们发现这样之后,就算n = 100,也只需要1ms:
方法三:动态规划
我们发现,其实这道题动态规划的
状态表达式就是由暴力搜索推出来的,
递归搜索是从上往下搜索,
再从下往上回溯,
其实得出的结果的过程就是在回溯的时候:
那我们可以不用搜索这个过程,直接从下往上递推,
这就是动态规划:
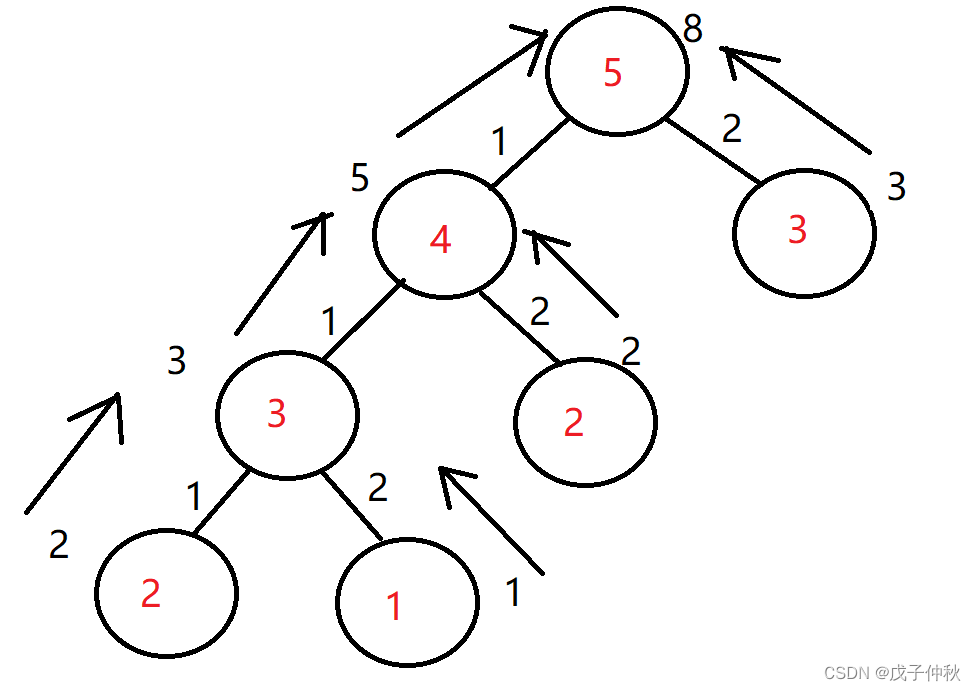
下面是代码实现:
代码
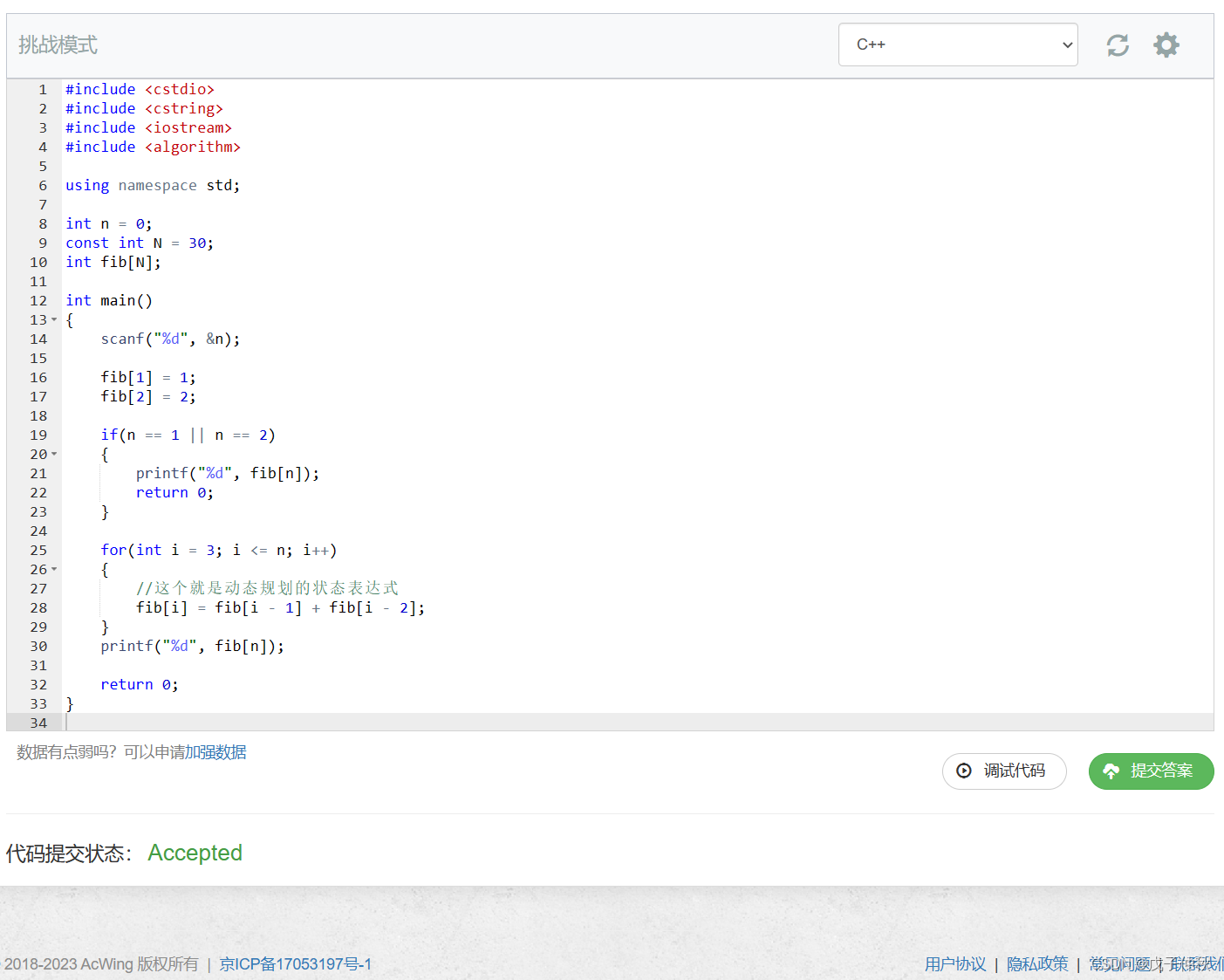
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int n = 0;
const int N = 30;
int fib[N];
int main()
{
scanf("%d", &n);
fib[1] = 1;
fib[2] = 2;
if(n == 1 || n == 2)
{
printf("%d", fib[n]);
return 0;
}
for(int i = 3; i <= n; i++)
{
//这个就是动态规划的状态表达式
fib[i] = fib[i - 1] + fib[i - 2];
}
printf("%d", fib[n]);
return 0;
}
AC !!!!!!!!!!
写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果喜欢本文的话,欢迎点赞和评论,写下你的见解。
如果想和我一起学习编程,不妨点个关注,我们一起学习,一同成长。
之后我还会输出更多高质量内容,欢迎收看。