🌇个人主页:_麦麦_
📚今日名言:喜你成疾,药石无医。——《玫瑰与鹿》

一、前言
在本篇文章,我们将为小伙伴们进行排序概念的基本讲解并具体讲解其中的两种基础排序:插入排序和希尔排序,希望小伙伴们能够从中有所收获!!!
二、正文
1.排序的概念及其运用
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2排序运用
看过排序的基础概念,可能有的小伙伴会问就算我学会了排序,但是在实际生活中有什么用吗?其实排序在生活中无处不在,比如说对一件商品不同维度的选择,又或者是对高校的排名,其实背后都存在着排序的思想,学好排序,能够帮助我们以另一种维度来观察生活中的方方面面并帮助我们更好地解决生活中的问题。


1.3常见的排序算法
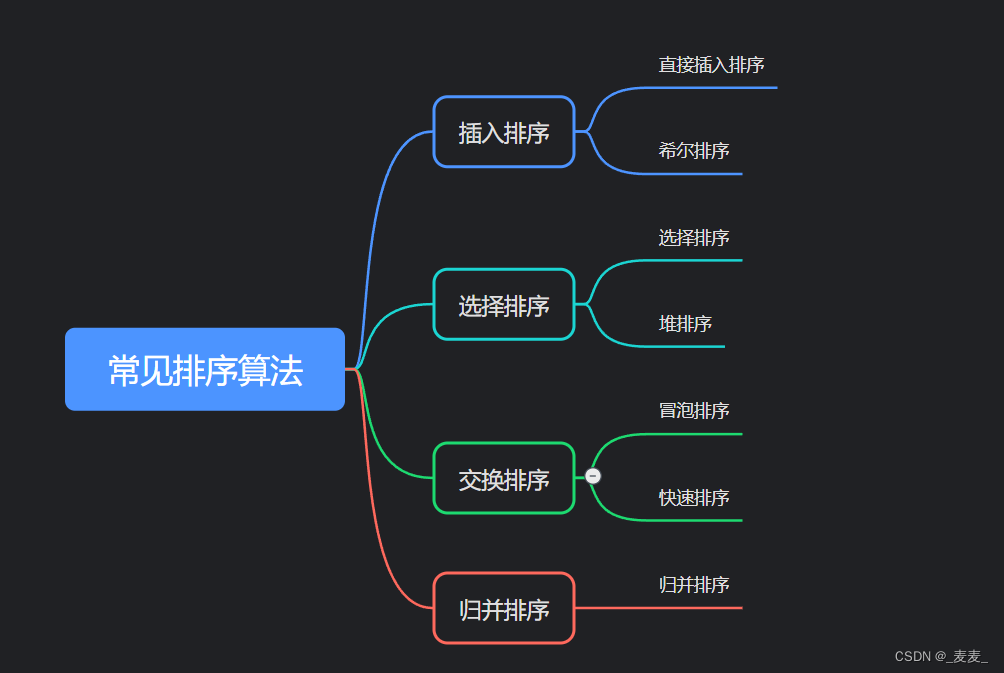
在数据结构这一块,我们常见的排序算法共有四种:
①插入排序:直接插入排序、希尔排序
②选择排序:选择排序、堆排序
③交换排序:冒泡排序、快速排序
④归并排序:归并排序
2.插入排序算法的实现
由于篇幅的关系,本篇我们主要介绍的是插入排序中的直接插入排序和希尔排序,而直接插入排序又常常被称为插入排序。
2.1插入排序
2.1.1基本思想
直接插入排序是一种简单的插入排序法
其基本思想是把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
实际中我们玩扑克牌时,就用了插入排序的思想。当你摸了一张新牌,自然而然地就会与手上已有的牌堆进行一一比较,在比较之后将其放入其应该所处的位置。所以我们可能并不知道插入排序是什么,但我们潜意识的做法恰恰就符合了插入排序。
2.1.2直接插入排序
用比较书面的语言来描述直接插入排序:当插入第i(i>=1)个元素时,前面的 array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与 array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
但这么说可能有的小伙伴会不太理解,那么通俗地来讲吧。现在在你面前有一个乱序的数组,我们的目的是要将这个乱序的数组调整为升序或者降序。
以升序为例叭,由于数组是无序的,因此我们需要从数组的第二个元素开始排序。为什么不是第一个呢,因为只有一个数字的的时候,你无法与其余元素比较,自然也就没有乱序一说,因此只有一个元素的时候我们就默认它是有序的。
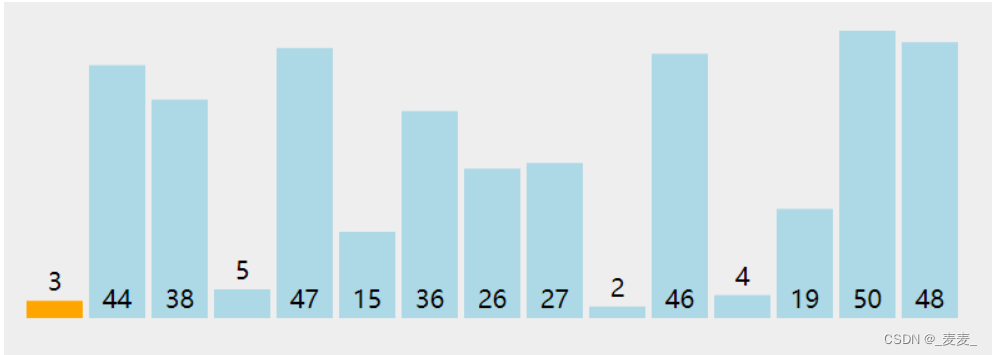
在理解完为什么要从第二个元素开始排序后,现在我们就要进行元素的依次插入和排序了。先是第二个元素的插入和排序,在下图中我们会发现第二个元素是44,44大于第一个元素3,因此不需要挪动第二个元素。紧接着就是第三个元素的插入和排序,我们发现第三个元素38小于第二个元素44,不符合我们升序的预期,因此将44挪动到38的位置,在第二、三个元素有序后,我们发现38大于3,也就是第一、二个元素也是有序的,因此就无需再挪动第一个元素的位置,这时候我们已经确认38应该所处的是数组中第二个元素的位置,因此我们只需将38插入到第二个元素的位置即可。相信看到这里的小伙伴对后续元素的插入与排序应该是信手拈来了,
接下来就是代码的书写了。在代码上,我们该如何实现上述元素的插入与排序呢?我们采取了两个主要的变量“des”和“end”,des就是我们所要插入的元素的初识下标,而end代表的是插入之前的序列的最后一个元素的下标,随着des的比较,end要不断向前移动,那么什么时候end的移动才会停止呢,也就是比较的结束,大致分为两种情况:①des所代表的元素大于end所代表的的元素 ②end已经来到序列的第一个元素,这时候des要么是第一个元素,或者是第二个元素。
具体图片和代码如下:
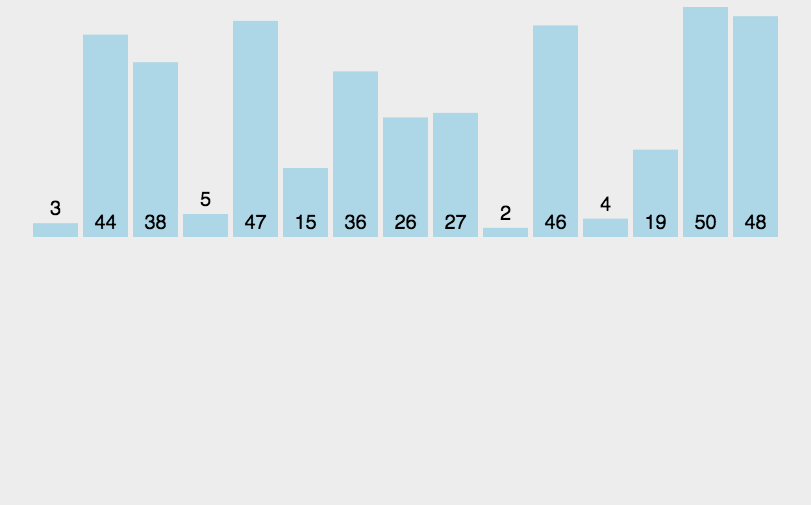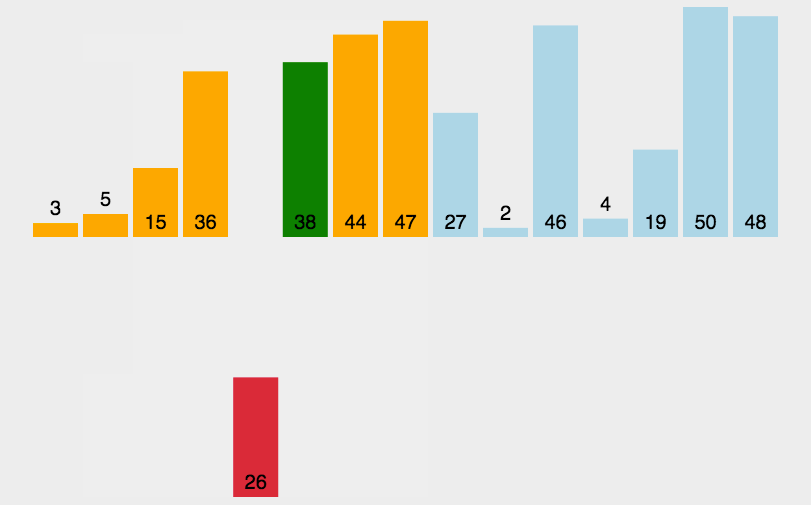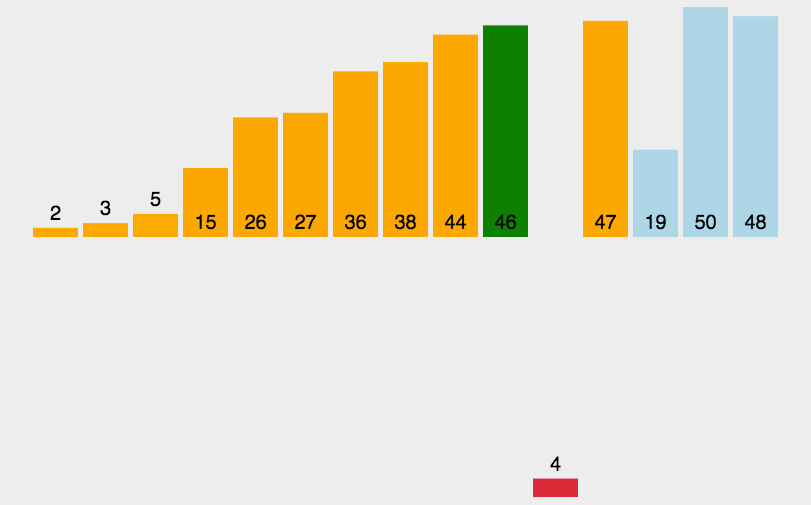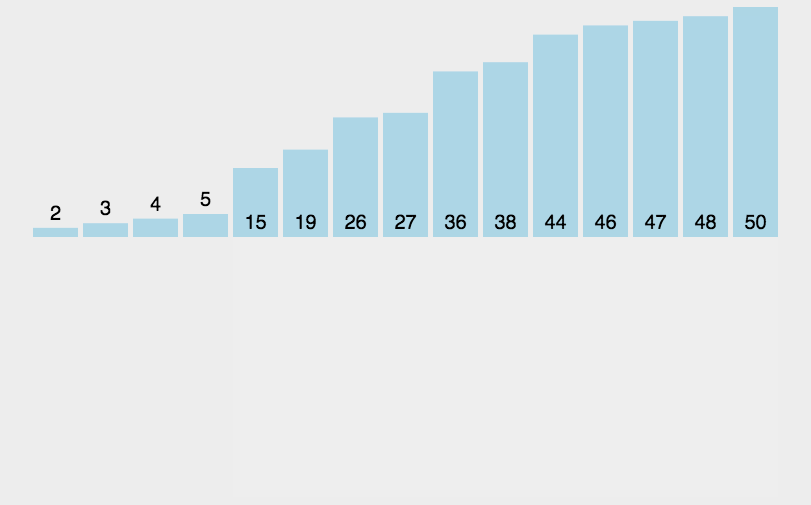
//插入排序[升序]
int* InsertSort(int* arr, int n)
{
//整体排序
for (int i = 1; i < n; i++)
{
int end = i - 1;
int des = arr[i];
//单趟排序
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
arr[end+1] = des;
}
}
}注:直接插入排序特性总结
①元素集合越接近有序,直接插入排序算法的时间效率越高
②时间复杂度:O(N^2)
③ 空间复杂度:O(1),它是一种稳定的排序算法
④ 稳定性:稳定
2.1.3希尔排序(缩小增量排序)
希尔排序法又称缩小增量法。
希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成整数个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后重复上述分组和排序的工作,当到达整数等于1时,所有记录在统一组内排好序。
通俗来讲,希尔排序就是多次的直接插入排序,不过除了最后一次直接插入排序之外的排序又和原本的直接插入排序有所不同。那么有的小伙伴看到这里可能就会问了为什么要进行多次的插入排序,单次的插入排序又和正常的插入排序不同在哪里呢?别着急,下面我们一个个回答。
先是为什么要多次的插入排序,看过上面对于插入排序的特性总结我们会发现,当元素的集合越接近有序,那么对其进行插入排序的时间效率就越高。因此希尔排序除了最后一次的排序是正常的插入排序之外的多次插入排序的目的就是不断的调整这个元素的集合,使其不断的接近有序。
紧接着就是希尔排序除最后一次插入排序之外的插入排序与正常插入排序的差异。通过上面对插入排序的学习,我们会发现对于一个乱序的数组的来说,一个元素若想来到正确的位置必须要与其余元素一一比较,也就是一步步的挪动,这种挪动在数组元素个数少的情况下尚可,但当这个数组的元素个数很多的时候,以升序来说,想象这个数组内最大的元素位于数组的第一个位置,那么是不是就要将这个元素与数组内其余元素一一比较以后,才能来到数组的最后一个位置,但当我们加大比较的步伐,也就是增大相比较的两个元素之间的距离,那么这个元素是不是就可以更快的来到它应该所处的位置。放置于飞行棋的情境之下,插入排序每次都掷出1,而哈希排序除了最后一次的插入排序掷出的点数是1,其余的插入排序所掷出的点数是都是大于1的,所以可想而知,哈希排序能够更快的到达排序的终点。
为了方便小伙伴们的理解,这部分代码共分为两部分:①固定步伐的直接插入排序②哈希排序。
先是固定步伐的直接插入排序,先让我们通过图片来直观的看到数组数组内的元素通过这种操作后的变化。
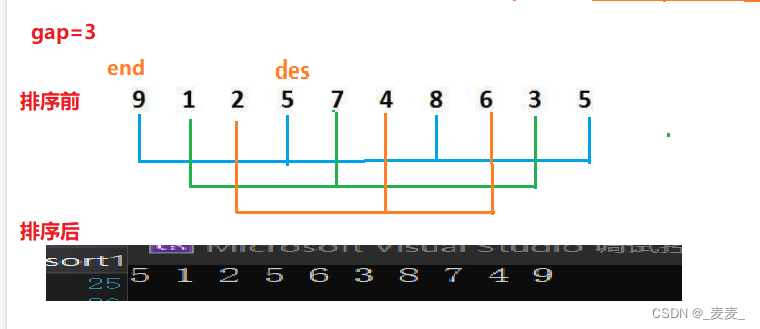
//固定步伐的直接插入排序[升序]
void ShellSort(int* arr, int n)
{
int gap = 3;
int end;
//有两种写法,看你要控制end,还是des
/*for (int i=0; i < n-gap; i++)
{
int end = i;
int des = arr[end + gap];
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = des;
}
}*/
for (int i = gap; i < n ; i++)
{
int end = i-gap;
int des = arr[end + gap];
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = des;
}
}
}接着就是希尔排序
上述的代码是gap=3的情况下的直接插入排序,那么对于希尔排序而言,我们该对gap该如何选择呢?对于不同gap值的插入排序来说,我们会发现:gap越大,元素跳得越快,数组越不接近有序;而gap越小,元素跳的越慢,数组越接近有序。由于数组的大小不定,因此希尔排序也没有一个合适gap值适用于所有数组,显然,这个gap值一定是动态变化的。
对于gap的动态变化,常见的有两种:
①令gap等于数组的元素个数,每次插入排序后令gap除等2
②另一种则是令gap等于数组的元素个数,不过每次插入排序后令gap除以3再加1
无论哪种处理都能使gap动态变化并最后等于1,对数组进行一次插入排序,达到最后想要的效果。
代码如下:
//希尔排序
void ShellSortPlus(int* arr, int n)
{
int gap=n;
int end;
while (gap > 1)
{
gap = gap / 2;
for (int i=0; i < n - gap;i++)//有两种写法,看你要控制end,还是des
{
int end = i;
int des = arr[end + gap];
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = des;
}
}
}
}三、测试代码
为了方便小伙伴们测试排序后的效果,为大家提供了测试的代码并包含排序的具体代码和包含的头文件。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
//插入排序[升序]
int* InsertSort(int* arr, int n)
{
//整体排序
for (int i = 1; i < n; i++)
{
int end = i - 1;
int des = arr[i];
//单趟排序
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
arr[end+1] = des;
}
}
}
//固定步伐的直接插入排序[升序]
void ShellSort(int* arr, int n)
{
int gap = 3;
int end;
//有两种写法,看你要控制end,还是des
/*for (int i=0; i < n-gap; i++)
{
int end = i;
int des = arr[end + gap];
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = des;
}
}*/
for (int i = gap; i < n ; i++)
{
int end = i-gap;
int des = arr[end + gap];
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = des;
}
}
}
//希尔排序
void ShellSortPlus(int* arr, int n)
{
int gap=n;
int end;
while (gap > 1)
{
gap = gap / 2;
for (int i=0; i < n - gap;i++)//有两种写法,看你要控制end,还是des
{
int end = i;
int des = arr[end + gap];
while (end >= 0)
{
if (des >= arr[end])
break;
if (des < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = des;
}
}
}
}
//打印排序好的数组
void PrintSort(int*arr,int n)
{
for(int i=0;i<n;i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
//测试插入排序
void Text1()
{
int arr[10] = { 25,14,8,7,18,24,16,57,98,105 };
InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintSort(arr, sizeof(arr) / sizeof(arr[0]));
}
//测试固定步伐的插入排序
void Text2()
{
int arr[10] = { 9,1,2,5,7,4,8,6,3,5};
ShellSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintSort(arr, sizeof(arr) / sizeof(arr[0]));
}
//测试希尔排序
void Text3()
{
int arr[10] = { 9,1,2,5,7,4,8,6,3,5 };
ShellSortPlus(arr, sizeof(arr) / sizeof(arr[0]));
PrintSort(arr, sizeof(arr) / sizeof(arr[0]));
}
int main()
{
//Text1();
Text2();
//Text3();
return 0;
}四、结语
到此为止,本期关于插入排序和希尔排序的讲解就告一段落了,在后续的文章里还有继续介绍其他的排序及其实现
关注我 _麦麦_分享更多干货:_麦麦_的博客_CSDN博客-领域博主
大家的「关注❤️ + 点赞👍 + 收藏⭐」就是我创作的最大动力!谢谢大家的支持,我们下期见!