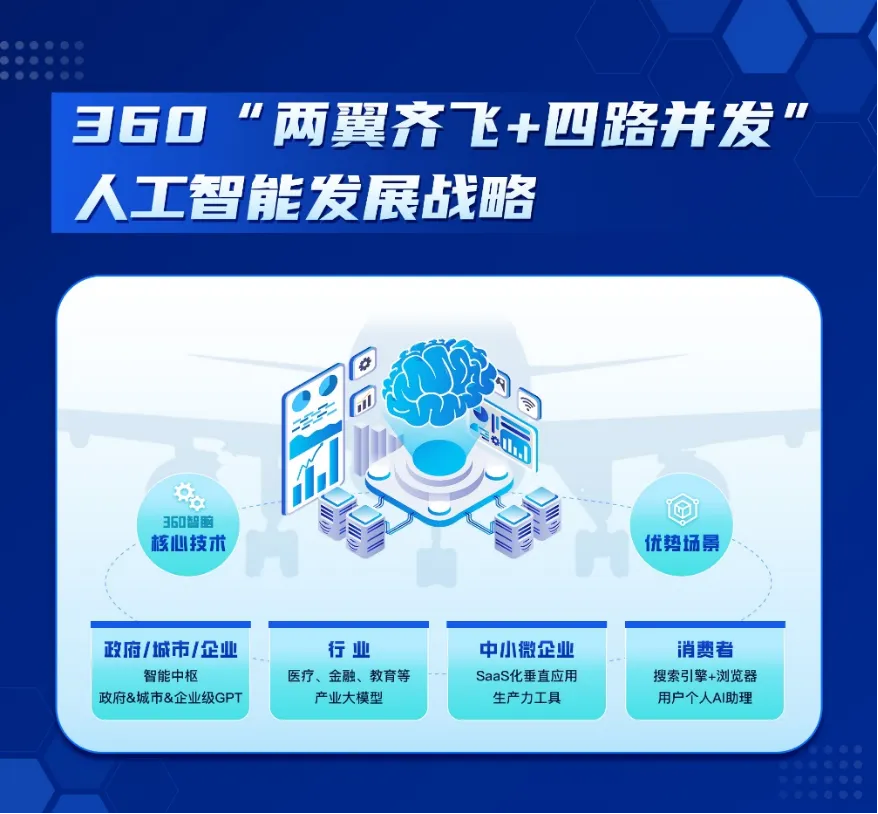
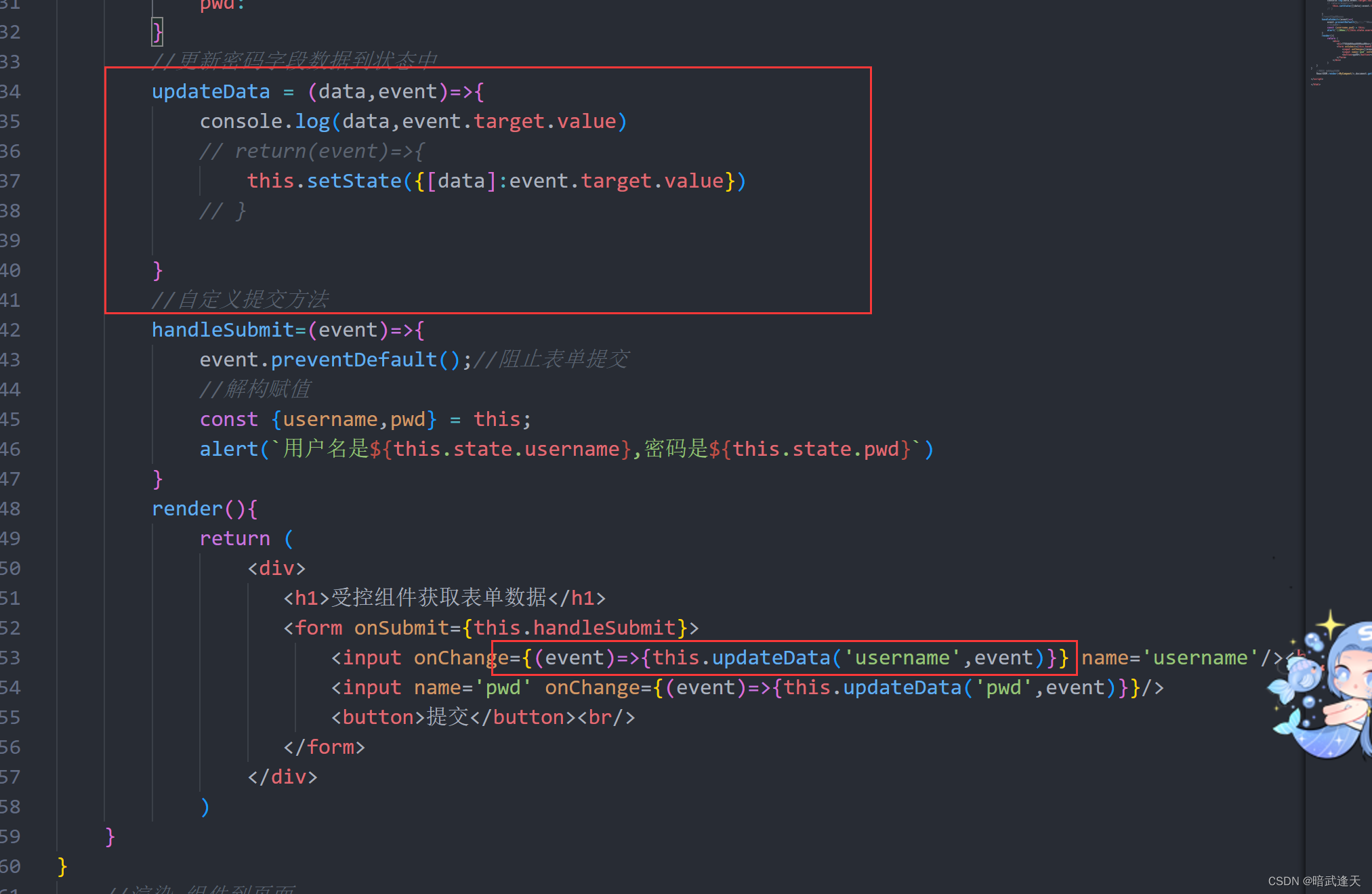
文章目录
- 一、实验目的
- 二、实验内容
- 1. 噪声图像及其直方图。
- 2. 空间噪声滤波器。
- 3. 逆滤波。
一、实验目的
- 了解一些常用随机噪声的生成方法。
- 掌握根据指定退化函数对图像进行退化的方法。
- 掌握当模糊图像只存在噪声时的几种滤波复原方法。
- 掌握当模糊图像同时存在线性退化和噪声时的几种滤波复原方法。
二、实验内容
1. 噪声图像及其直方图。
图1显示了一幅测试图像,它由简单的恒定区域组成,且其从黑到近似于白仅有3个灰度级增长跨度,非常适合于对附加在图像上的各种噪声成分特性的视觉分析。请进行以下操作:
(1) 对图1叠加高斯噪声,参数
a
=
0
a=0
a=0,
b
=
0.02
b=0.02
b=0.02 ,并求含噪声图像的直方图。
(2) 对图1叠加瑞利噪声,参数
a
=
0
a=0
a=0,
b
=
0.01
b=0.01
b=0.01 ,并求含噪声图像的直方图。
(3) 对图1叠加爱尔兰噪声,参数
a
=
25
a=25
a=25,
b
=
2
b=2
b=2 ,并求含噪声图像的直方图。
(4) 对图1叠加指数噪声,参数
a
=
25
a=25
a=25,并求含噪声图像的直方图。
(5) 对图1叠加均匀噪声,参数
a
=
0
a=0
a=0,
b
=
0.15
b=0.15
b=0.15 ,并求含噪声图像的直方图。
(6) 对图1叠加椒盐噪声,参数
a
=
0.05
a=0.05
a=0.05,
b
=
0.05
b=0.05
b=0.05 ,并求含噪声图像的直方图。提示:加椒盐噪声时,要结合find函数。找出生成的噪声R中值为0的点,将原图像中相应位置置0;找出生成的噪声R中值为1的点,将原图像中相应位置置1,以完成椒盐噪声的添加。

f=imread('1.测试图像.tif');
f=im2double(f);
[M,N]=size(f);
R1=imnoise2('gaussian',M,N,0,0.02);
y1=f+R1;
figure; subplot(251);imshow(y1);subplot(256);imhist(y1);
imwrite(y1,'加高斯噪声后的图像.tif');
%---------------rayleigh噪声-----------------------------%
R2=imnoise2('rayleigh', M,N,0,0.01);
y2=f+R2;
subplot(252);imshow(y2);subplot(257);imhist(y2);
imwrite(y2,'加高斯噪声后的图像.tif');
%--------------------伽马(爱尔兰)噪声-----------------------------%
R3=imnoise2('erlang',M,N,25,2);
y3=f+R3;
subplot(253);imshow(y3);subplot(258);imhist(y3);
imwrite(y3,'加伽马(爱尔兰)噪声后的图像.tif');
%--------------------指数噪声-----------------------------%
R4=imnoise2('exponential',M,N,25);
y4=f+R4;
subplot(254);imshow(y4);subplot(259);imhist(y4);
imwrite(y4,'加指数噪声后的图像.tif');
%--------------------均匀噪声-----------------------------%
R5=imnoise2('uniform',M,N,0,0.15);
y5=f+R5;
subplot(255);imshow(y5);subplot(2,5,10);imhist(y5);
imwrite(y5,'加均匀噪声后的图像.tif');

%--------------------椒盐噪声-----------------------------%
R6=imnoise2('salt & pepper',M,N,0.05,0.05);
p=find(R6==0);
y6=f;
y6(p)=0.01;
s=find(R6==1);
y6(s)=0.99;
y6=im2uint8(y6);
figure; imshow(y6);
figure;imshow(y6);imhist(y6)

2. 空间噪声滤波器。
图2是一幅被加性均匀噪声和椒盐噪声污染的图像,请进行以下实验:
(1) 用大小为
5
×
5
5\times 5
5×5 的算术平均滤波器对图2进行滤波。
(2) 用大小为
5
×
5
5\times 5
5×5 的几何均值滤波器对图2进行滤波。
(3) 用大小为
5
×
5
5\times 5
5×5 的中值滤波器对图2进行滤波。
(4) 用大小为
5
×
5
5\times 5
5×5 且
d
=
6
d=6
d=6 的修正阿尔法均值滤波器对图2进行滤波。

答:
(1)
(2)
gp = zeros(M+4, N+4);
gp(3:M+2,3:N+2) = f;
gp(1,:) = gp(3,:); %用图像最外层的值扩展
gp(2,:) = gp(3,:);
gp(M+4,:)=gp(M+2,:);
gp(M+3,:)=gp(M+2,:);
gp(:,2)=gp(:,3);
gp(:,1)=gp(:,3);
gp(:,N+4)=gp(:,N+2);
gp(:,N+3)=gp(:,N+2);
g2 = zeros(M, N);
for x = 3:M+2
for y = 3:N+2
g_gmf = 1;
for i = -2:2
for j = -2:2
g_gmf = g_gmf*gp(x+i,y+j);
end
end
g2(x-2,y-2)=g_gmf;
end
end
g2=g2.^(1/9);
g2=im2uint8(g2);
figure; imshow(g2);
imwrite(g2,'5×5 几何均值滤波图像.tif');

% 1. 读取图像
img = imread('2.被加性均匀噪声和椒盐噪声污染的图像.tif');
% 2. 检查图像是否为彩色图像,如果是,则将其转换为灰度图像
if ndims(img) == 3
img_gray = rgb2gray(img);
else
img_gray = img;
end
% 3. 对灰度图像应用5x5中值滤波器
filtered_img = medfilt2(img_gray, [5, 5]);
% 4. 显示原始图像和处理后的图像
figure;
subplot(1, 2, 1);
imshow(img_gray);
title('Original Image');
subplot(1, 2, 2);
imshow(filtered_img);
title('Filtered Image with Median Filter');
% 5. 保存处理后的图像
imwrite(filtered_img, 'output_image.jpg');

% 1. 读取图像
img = imread('input_image.jpg');
% 2. 检查图像是否为彩色图像,如果是,则将其转换为灰度图像
if ndims(img) == 3
img_gray = rgb2gray(img);
else
img_gray = img;
end
% 3. 对灰度图像应用5x5修正阿尔法均值滤波器 (d = 6)
filtered_img = modified_alpha_trimmed_mean_filter(img_gray, 5, 6);
% 4. 显示原始图像和处理后的图像
figure;
subplot(1, 2, 1);
imshow(img_gray);
title('Original Image');
subplot(1, 2, 2);
imshow(filtered_img);
title('Filtered Image with Modified Alpha-trimmed Mean Filter');
% 5. 保存处理后的图像
imwrite(filtered_img, 'output_image.jpg');
function output_img = modified_alpha_trimmed_mean_filter(img, filter_size, d)
img = double(img);
[rows, cols] = size(img);
output_img = zeros(rows, cols);
pad_size = floor(filter_size / 2);
padded_img = padarray(img, [pad_size pad_size], 'replicate');
for i = 1:rows
for j = 1:cols
window = padded_img(i:i+filter_size-1, j:j+filter_size-1);
window_sorted = sort(window(:));
output_img(i, j) = mean(window_sorted(d/2 + 1:end - d/2));
end
end
output_img = uint8(output_img);
end

3. 逆滤波。
图3为一幅大小为480×480的模糊图像,其退化函数如式(1)所示:
H
(
u
,
v
)
=
e
−
k
[
(
u
−
M
/
2
)
2
+
(
v
−
N
/
2
)
2
]
5
/
6
(1)
H(u,v)={{\text{e}}^{-k{{[{{(u-M/2)}^{2}}+{{(v-N/2)}^{2}}]}^{5/6}}}}\tag1
H(u,v)=e−k[(u−M/2)2+(v−N/2)2]5/6(1)
其中,
k
=
0.0025
k=0.0025
k=0.0025,
M
=
N
=
480
M=N=480
M=N=480。请根据式(2)及以下要求对图3图像进行逆滤波操作:
F
^
(
u
,
v
)
=
G
(
u
,
v
)
H
(
u
,
v
)
(2)
\hat{F}(u,v)=\frac{G(u,v)}{H(u,v)}\tag2
F^(u,v)=H(u,v)G(u,v)(2)
(1) 请对图3直接进行逆滤波(全滤波)。
(2) 使用一个阶数为10的巴特沃斯低通函数来对比值 G ( u , v ) H ( u , v ) \frac{G(u,v)}{H(u,v)} H(u,v)G(u,v) 实现截止,截止半径分别设置为40、70和85。
(3) 对比分析实验结果。

答:
(1)
close all; clear all; clc;
f = imread('3.大小为480×480的模糊图像.tif');
figure; imshow(f);
f=im2double(f);
[M, N] = size(f);
F= fft2(f);
Fc=fftshift(F);
[v, u]=meshgrid(1:N, 1:M);
H=exp(-0.0025*((u-M/2).^2+(v-N/2).^2).^(5/6));
G=Fc./(H+eps);
G1=ifftshift(G);
g1=ifft2(G1);
figure; imshow(g1, []);

(2)
%---------截止半径设置为 40---------%
H2= zeros(M,N);
D0 = 40;
for x = 1:1:M
for y = 1:1:N
D = ((x-M/2)^2 + (y-N/2)^2)^(0.5);
H2(x,y) = 1/(1+(D/D0)^20);
end
end
G2=G.*H2;
G2=ifftshift(G2);
g2=ifft2(G2);
subplot(131); imshow(g2, []);title('截止半径为40');
%---------截止半径设置为 70---------%
H2= zeros(M,N);
D0 = 70;
for x = 1:1:M
for y = 1:1:N
D = ((x-M/2)^2 + (y-N/2)^2)^(0.5);
H2(x,y) = 1/(1+(D/D0)^20);
end
end
G2=G.*H2;
G2=ifftshift(G2);
g2=ifft2(G2);
subplot(132); imshow(g2, []);title('截止半径为70');
%---------截止半径设置为 85---------%
H2= zeros(M,N);
D0 = 85;
for x = 1:1:M
for y = 1:1:N
D = ((x-M/2)^2 + (y-N/2)^2)^(0.5);
H2(x,y) = 1/(1+(D/D0)^20);
end
end
G2=G.*H2;
G2=ifftshift(G2);
g2=ifft2(G2);
subplot(133); imshow(g2, []);title('截止半径为85');

(3)
当退化函数为0或者是很小的值,直接使用逆滤波公式会导致
N
(
u
,
v
)
/
H
(
u
,
v
)
N\left( u,v \right)/H\left( u,v \right)
N(u,v)/H(u,v) 对
F
∧
(
u
,
v
)
\overset{\wedge }{\mathop{F}}\,(u,v)
F∧(u,v) 起到支配作用。频域率转变为空间域就会产生错误的结果。