首先从目标函数开始

假设下图反映了 投入多少广告费，产生了多少销售量的关系

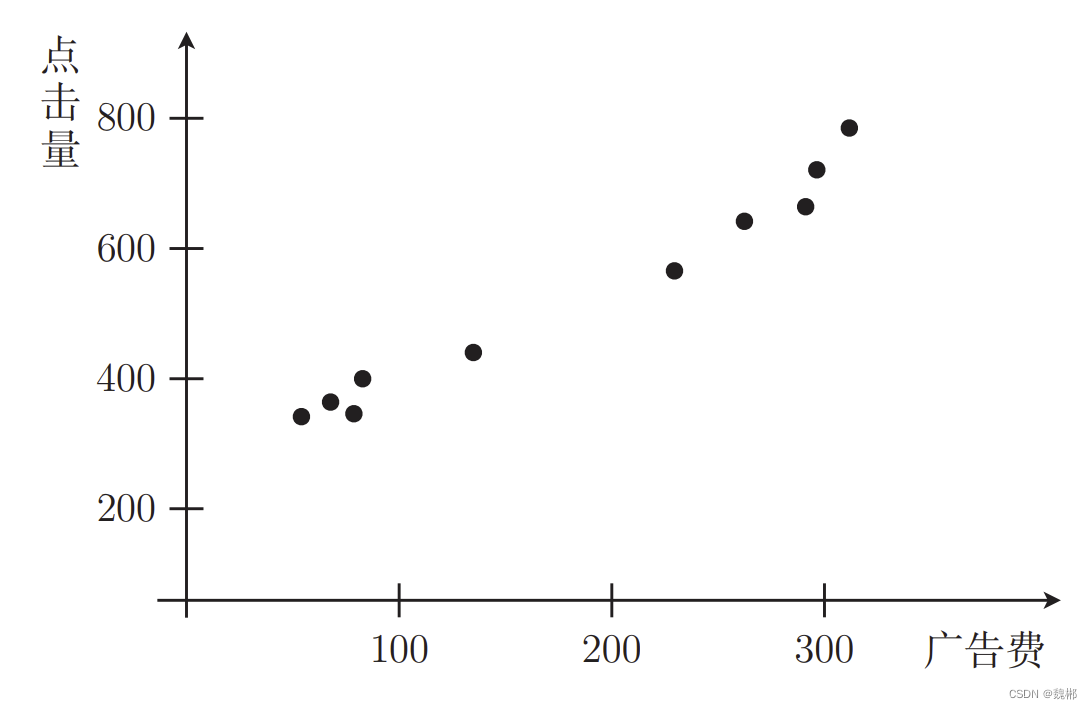
图中每个点都是一个数据，每个点都有x，y的坐标，记作x**（i），y**（i），i表示第几个数据。
那么问题就是找到一个函数去描述这个趋势，如此才能预测未来。

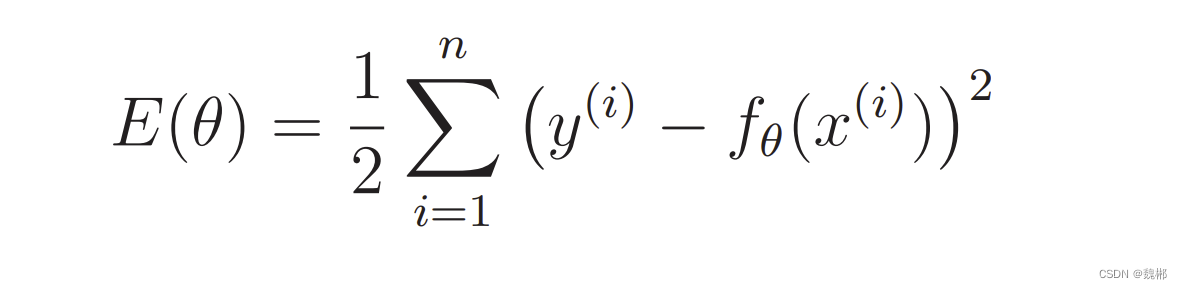
• 先解释 y-f（x）的意思 首先每个数据都有x坐标和y坐标，现在要求函数，就是我设个函数，给个x，然后这个函数的y和数据的y差多少，如果离得很近，那么差距几乎就是0，那么这个函数就可以表示这个趋势了
• 
• z就是 这个数据实际的y 和 随便搞了一个函数的y的差值，只要不断调整这个函数使得差值越来越小，那么我们最终就可以找到 这个函数了
• y和x上面都是 小i 代表不同数据（就是散点图中的点），有n个数据，那么就是这样减n次，然后把结果加起来，看看是否接近0，就知道这函数能不能代表这个趋势
• 为什么要平方，万一出现下图这种情况，负值和正值 最终相加虽然结果趋于0，但是明显这个函数无法代表这个图的趋势
• 
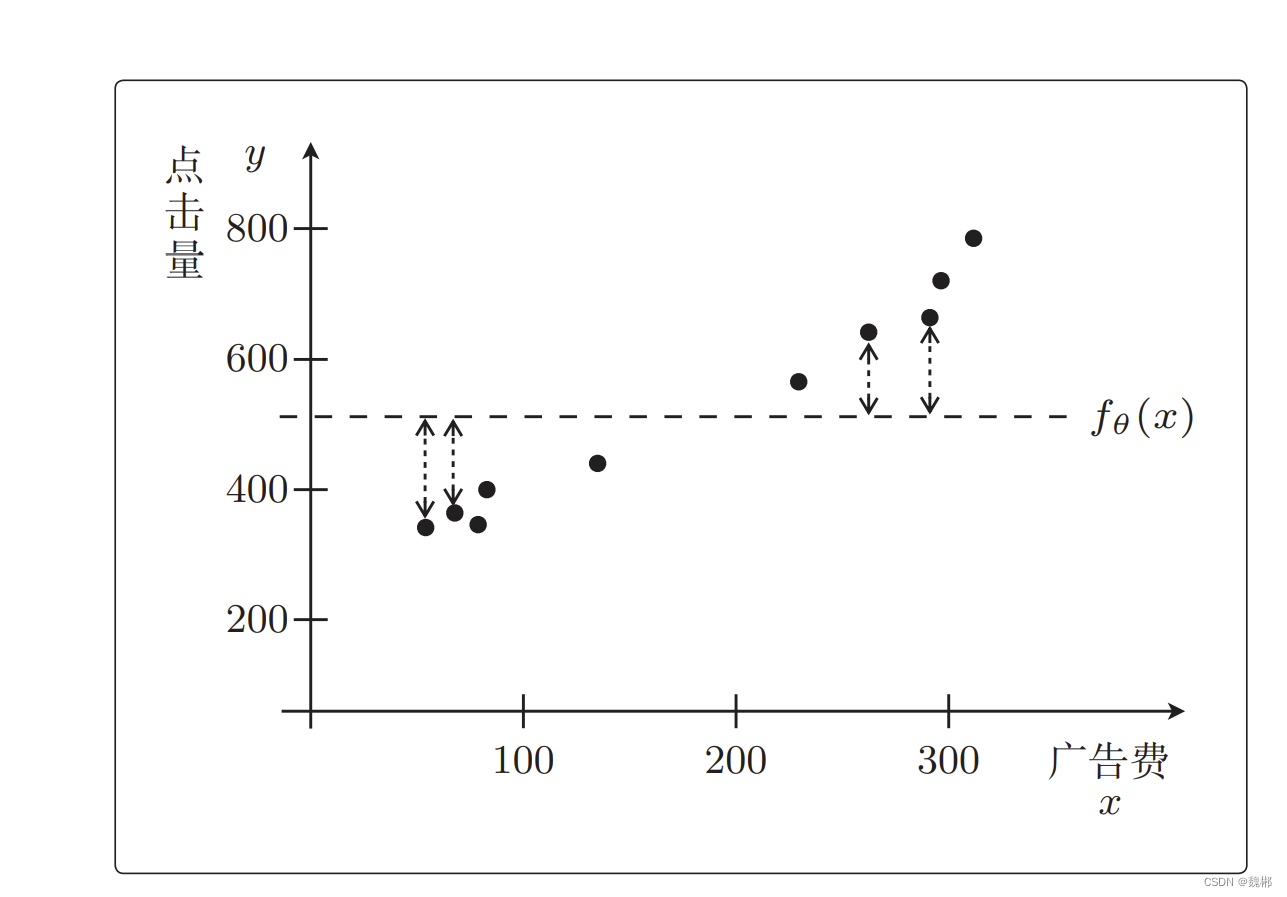
• 之所以加二分之一，和用平方不用绝对值 都是为了方便后面微分计算
• E（θ）又称为目标函数，解决最优化问题

梯度下降法

求最小值
A：=B 表示用B的结果在代入到A 继续运算

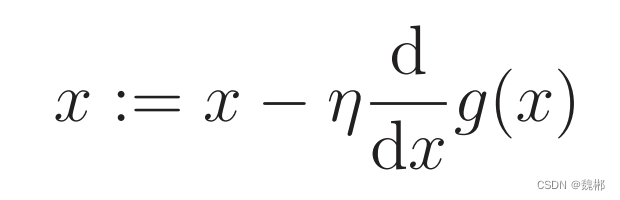
η是学习率
假设g（x）= （x-1）**2
g（x）的导数就是2x-2
设学习率为1，x从3开始
运算如下


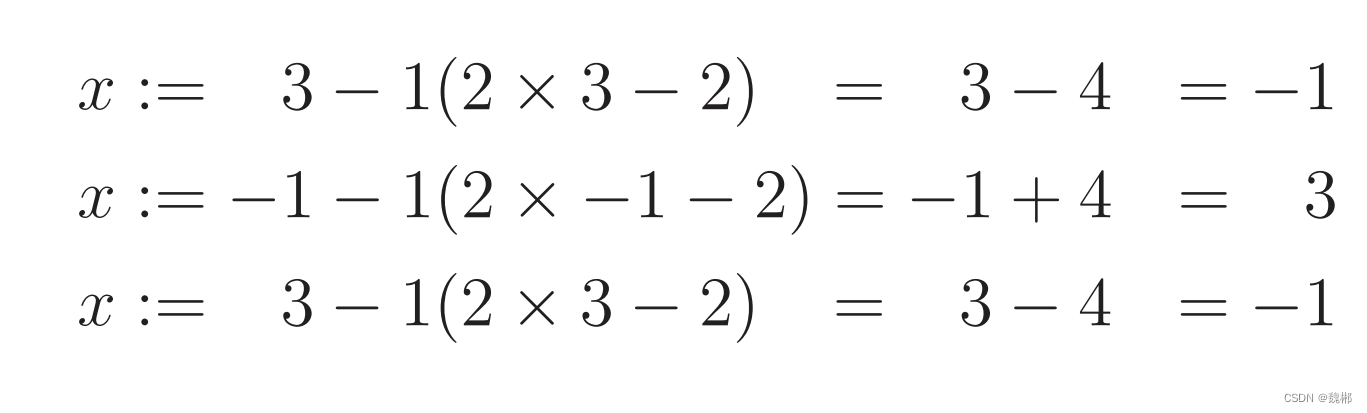
可以看到 值反复横跳，无法求到最小值
设η为0.1，运算如下


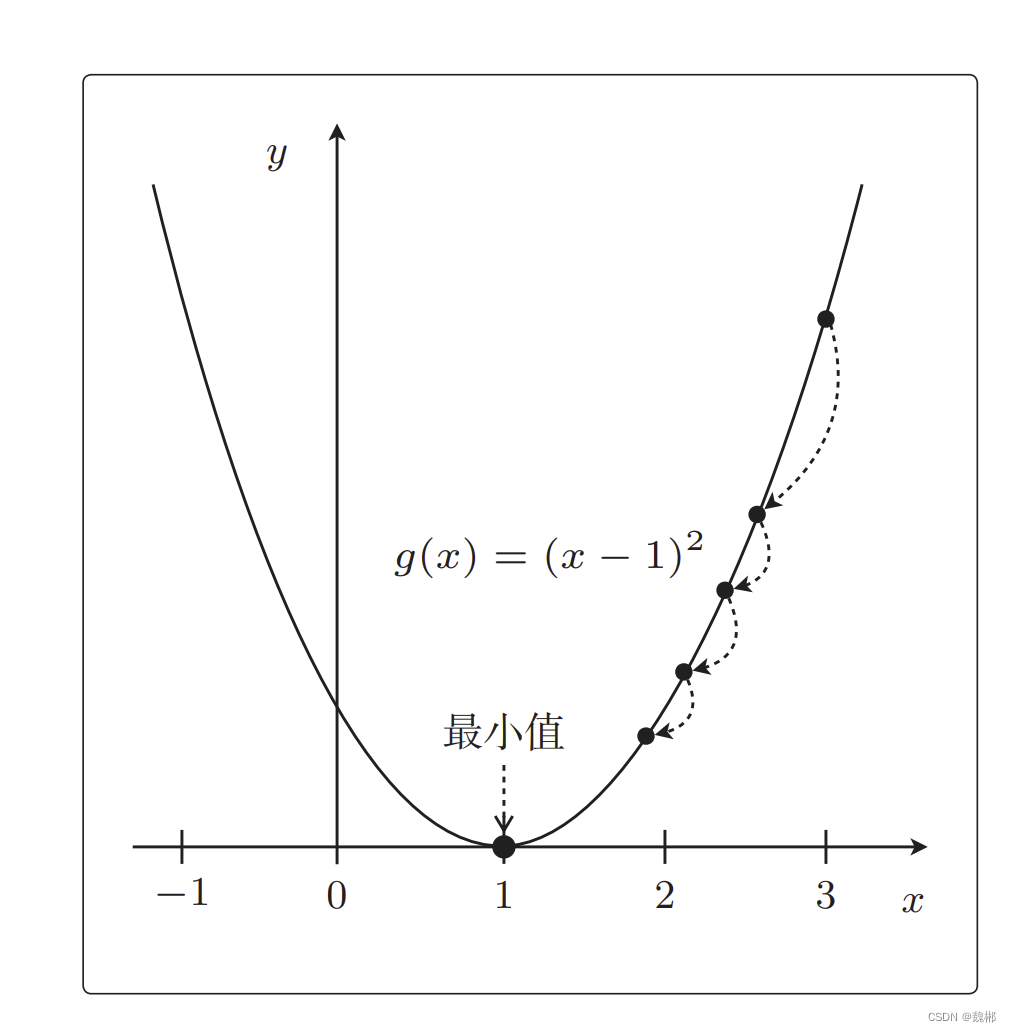
可以求到最小值

结合两个公式，让目标函数梯度下降

设f（x）= θ0+θ1*x
求出θ的最小值


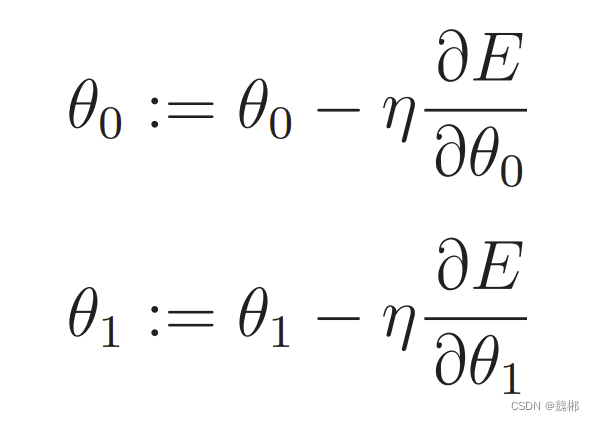
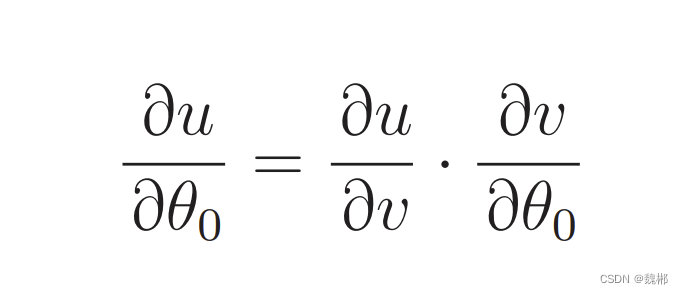
一个一个求，求θ0，等于先求E中f的偏导数 在求f（x）中θ0的偏导数



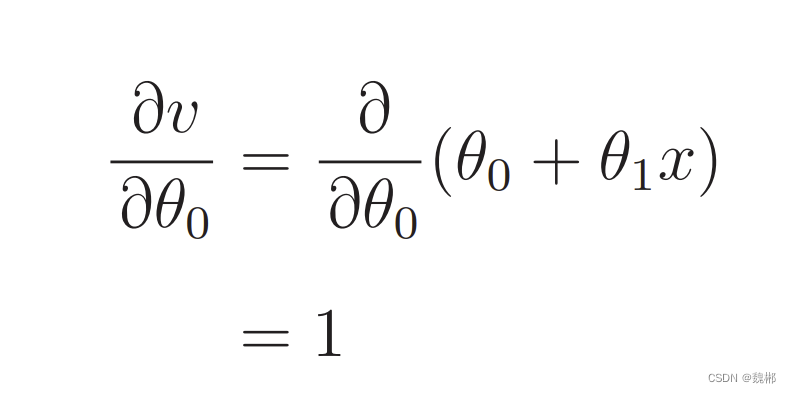
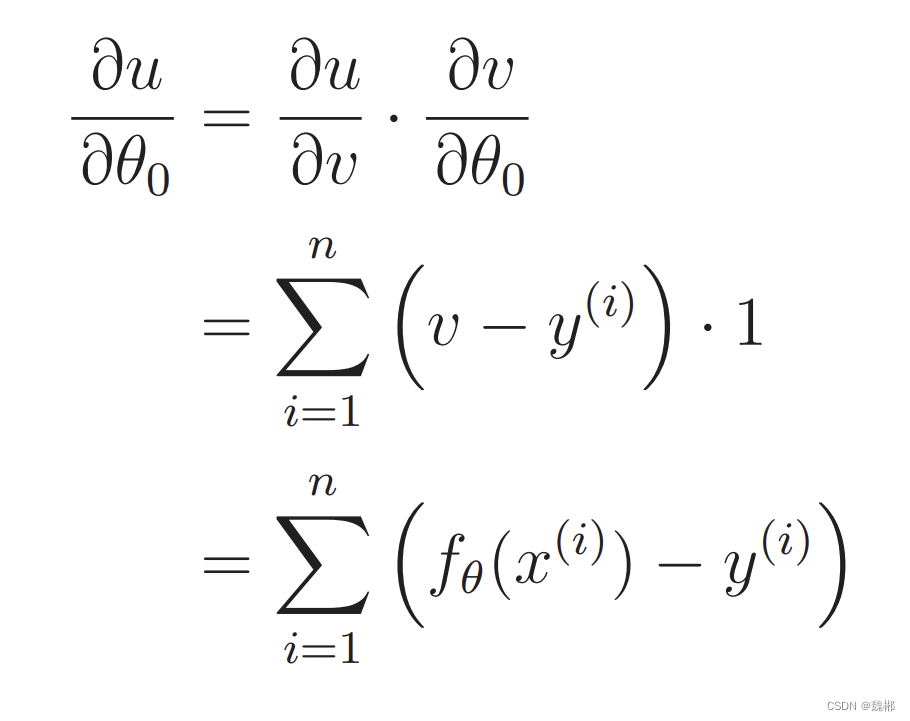
求y的也同理
记住E目标函数的偏导数是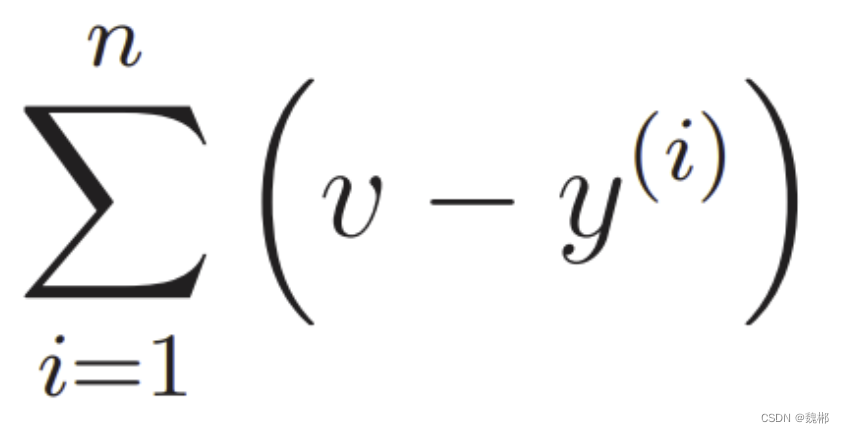
现在只需要求函数中θ的偏导数，在乘这个就行了

多项式回归，多重回归

刚刚公式f（x）里只有一个x，实际问题往往比较复杂，不能用一个未知数表示

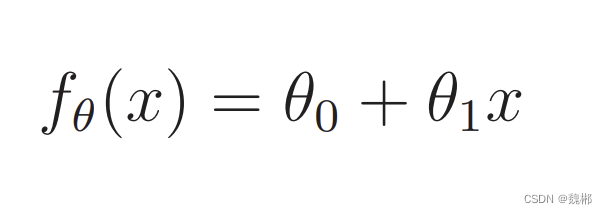
现在要变成这样


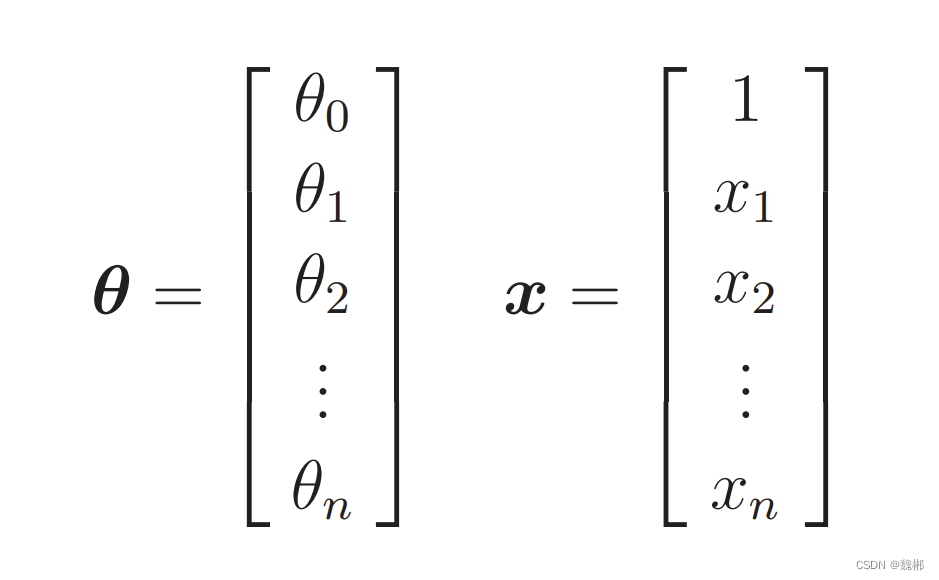
用向量矩阵来描述这个函数，把θ转置与x相乘就可以得到上图函数的公式

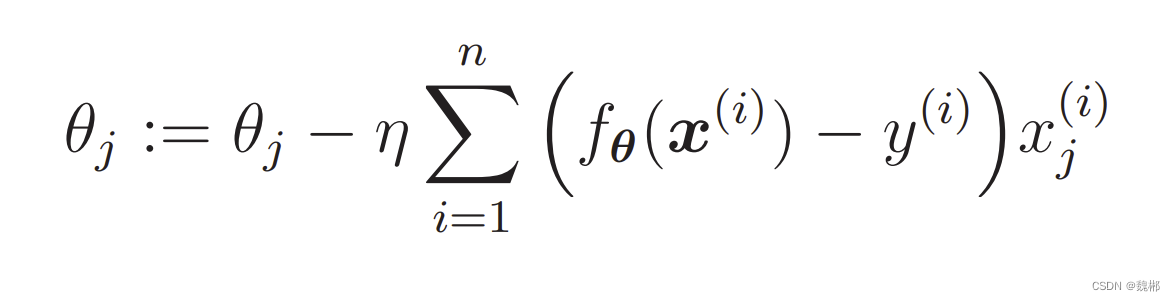
由于求第几个θ的偏导数，那么第几个x就是它的常数，那么结果也就是也就是尝数，所以θ的偏导数结果直接等于对应位置的x
拿这个去乘固定的E的偏导数，然后在把所有数据也就是i，比如有n个数据，那么就这样求n次，把n次的结果加起来，乘以学习率，在用原θ值减去这个值，赋值给θ称成为新的θ值，在用这个值减去上述计算。。。。。。。。直到求到该θ的最小值
如果有n个数据，求每个西塔需要求n次梯度下降，每次梯度下降要把每个数据与函数的结果求偏导计算一遍，n个西塔，每个n次梯度下降，每次梯度下降n个训练数据要计算。。。。。。
结果就是： 计算量太大太大太大啦！！！！！！
第二个问题，局部最优解
刚刚说这个的时候设置的是x为3


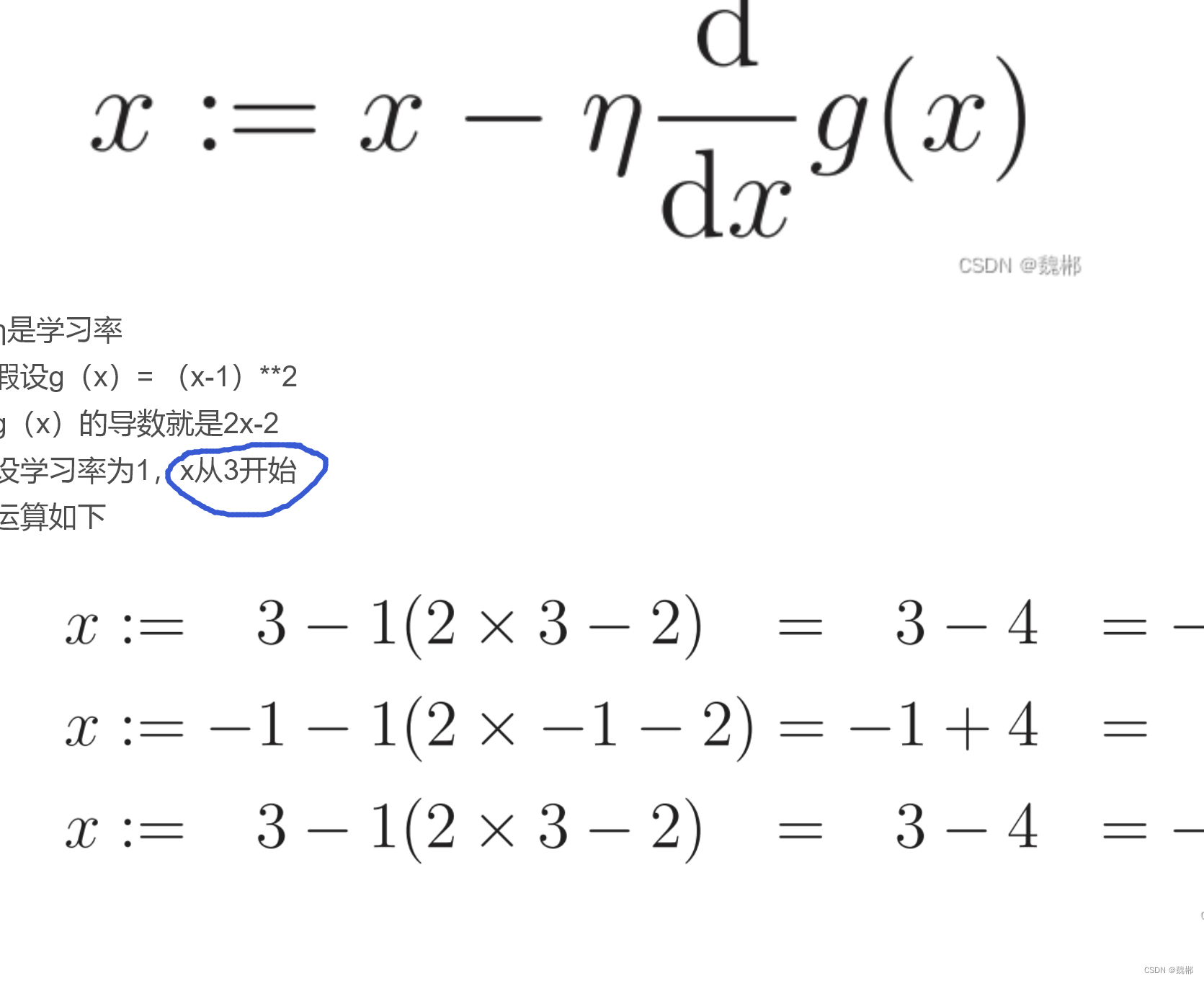
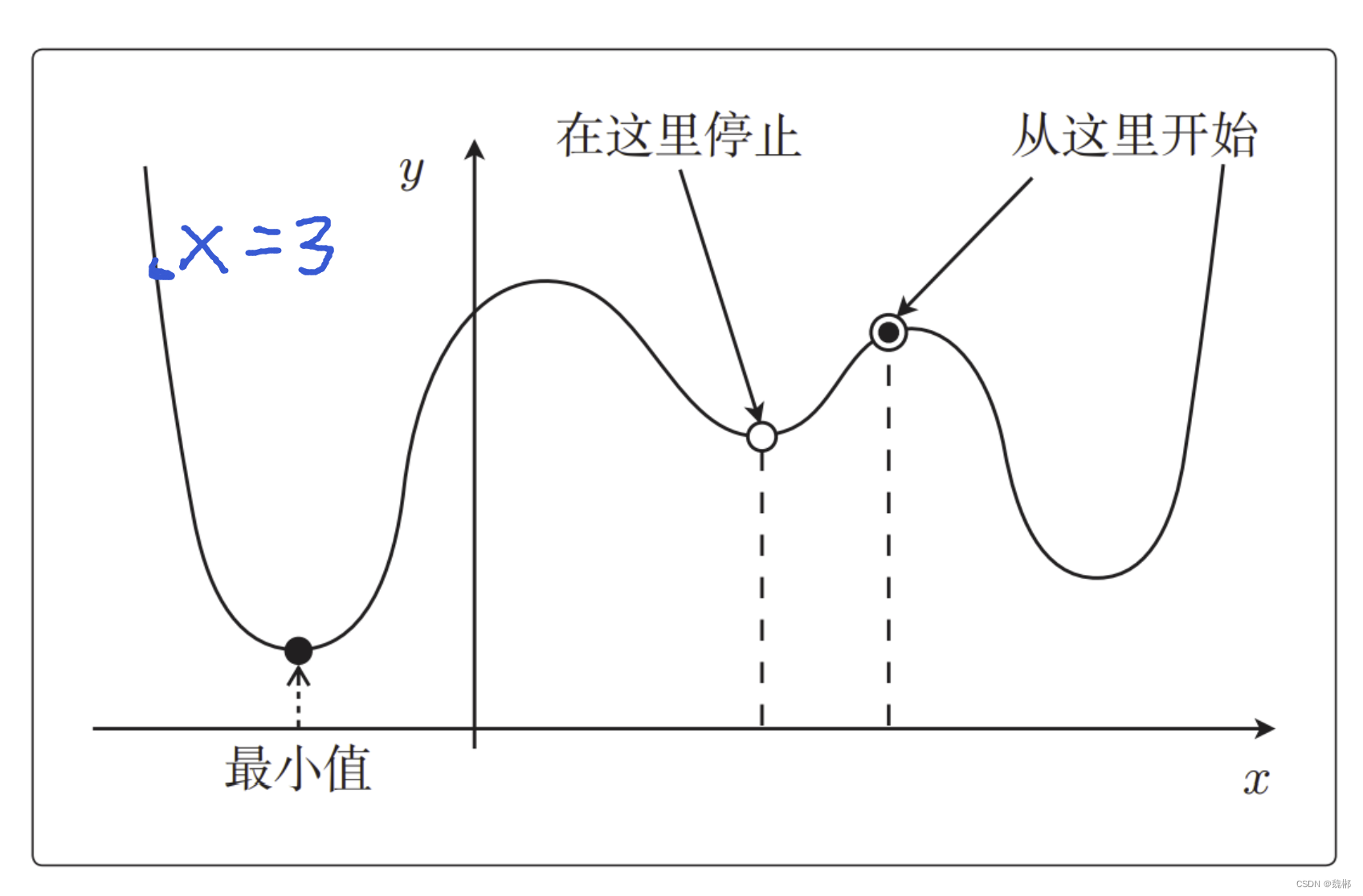
那么如果x在那个点上，就求不到最小值了

问题1	问题2
计算量太大	局部最优解

解决办法：随机梯度下降

随机一个数据

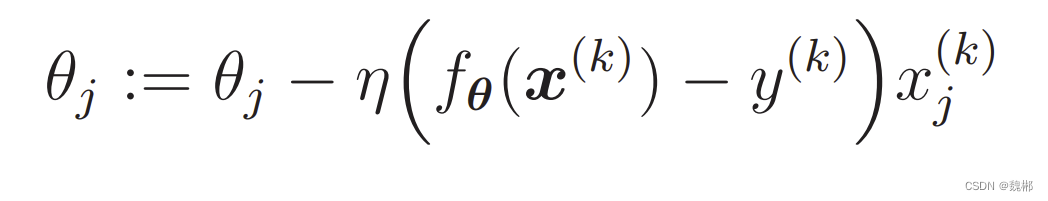
随机多个数据，也叫 小批量梯度下降法

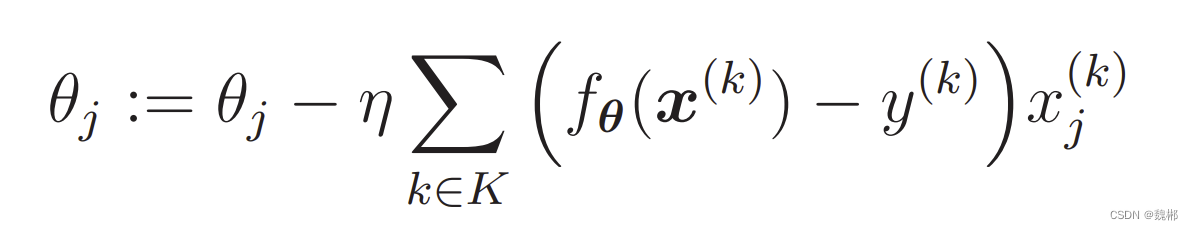
i是 所以训练数据，然后把差值加起来 找到总差值最小的，即为最优解
k 现在是只找一个数据，然后看这个函数关于这个数据的差值就为最优解，之前每次梯度下降都要把所有训练数据计算一遍，现在只计算一次，计算量大大降低
K集合 同理，不过不是一个训练数据，而是随机找几个训练数据
η学习率设置为多少合适还是得试