文章目录
- 前言
- 一、空间坐标变换原理
- 1. 位姿描述
- 2. 欧拉角与四元数
- 二、ROS中python实现坐标变换
- 1. 坐标msg消息载体
- 2. 乌龟跟随的程序实现
- 总结
前言

ROS给开发者们提供了很多集成度很高的开发工具,例如rviz和gazebo。rviz是三维可视化工具,可以显示图像、模型、路径等信息,但是前提都是这些数据已经以话题、参数的形式发布,rviz做的事情就是订阅这些数据,并完成可视化的渲染,这次博主主要依托rviz的三维平台,学习坐标变换和机器人三维建模
一、空间坐标变换原理
1. 位姿描述
学习位姿描述之前首先要了解矩阵的本质。如果我们将矩阵和函数联想起来,将它理解成一种映射变化,那么矩阵的本质是在描述一种对基向量的空间变换,而行列式表达的正好是基向量变换后围成的面积
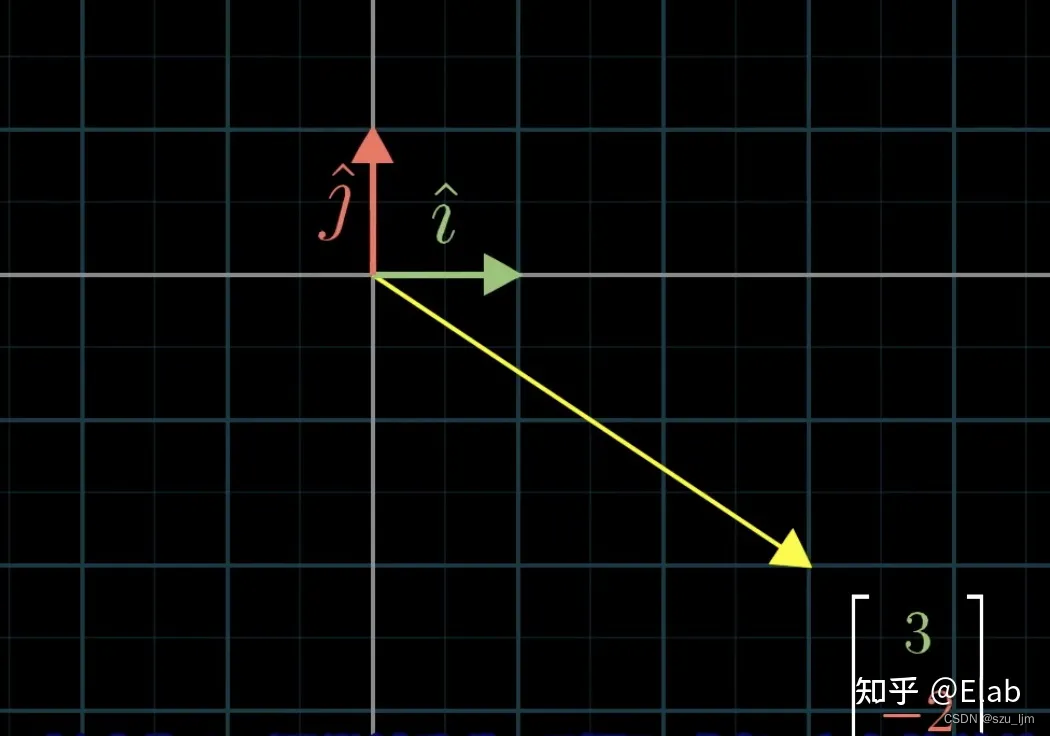
i
\boldsymbol{i}
i 和
j
\boldsymbol{j}
j 是成形二维平面的最简单的一对基,而矩阵关注的就是对这两对基向量的线性变换,一种类似于函数的作用
a
⃗
=
f
(
b
⃗
)
\vec{a} = f(\vec{b})
a=f(b)
比如,
[
i
j
]
\left[ \begin{array}{ccc} i \\ j \end{array} \right ]
[ij] 这个基经过
[
3
2
−
2
1
]
\left[ \begin{array}{ccc} 3 & 2\\ -2 & 1 \end{array} \right ]
[3−221] 的映射,
i
i
i 变成了
(
3
,
−
2
)
(3,-2)
(3,−2) 这个新的基向量,
j
j
j 变为
(
2
,
1
)
(2,1)
(2,1) 这个新的基向量,整个二维平面就发生了如下变化:
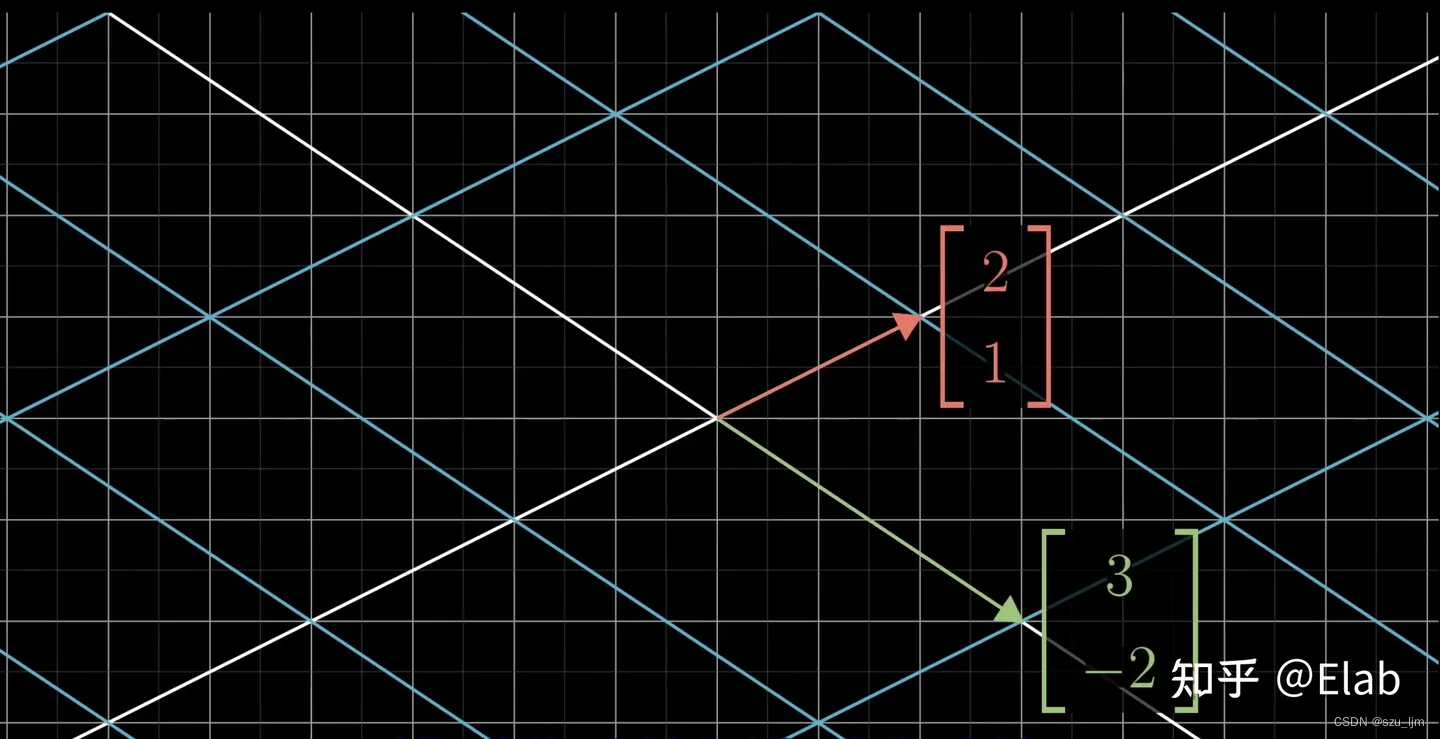
我们将变化后的2个基向量按如下方式放入矩阵,这样这个矩阵
[
3
2
−
2
1
]
\left[ \begin{array}{ccc} 3 & 2\\ -2 & 1 \end{array} \right ]
[3−221] 就表示了一次对二维空间的变换映射,其中的2个列分别为经过变换后的
i
\boldsymbol{i}
i 和
j
\boldsymbol{j}
j。
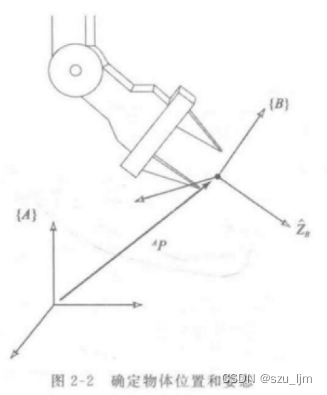
我们来讲讲位姿,位姿代表位置和姿态。任何一个刚体在空间坐标系
O
X
Y
Z
OXYZ
OXYZ 中可以用位置和姿态来精确、唯一地表示其位置状态。对于直角坐标系{A},空间任一点
p
p
p 的位置可以用3x1的列矢量
A
P
^{A}P
AP 来表示。
A
P
=
[
p
x
p
y
p
z
]
^{A}P = \left[ \begin{array}{ccc} p_{x}\\ p_{y}\\ p_{z} \end{array} \right ]
AP=
pxpypz
假设主坐标系为
A
{A}
A ,我们用
X
B
ˆ
、
Y
B
ˆ
、
Z
B
ˆ
\^{X_{B}}、\^{Y_{B}}、\^{Z_{B}}
XBˆ、YBˆ、ZBˆ来表示另一个坐标系
B
{B}
B 三个轴的单位向量,则坐标系
B
{B}
B 相对于坐标系
A
{A}
A 的旋转矩阵可以表达为
B
A
R
=
(
A
X
B
ˆ
A
Y
B
ˆ
A
Z
B
ˆ
)
=
[
X
B
ˆ
∙
X
A
ˆ
Y
B
ˆ
∙
X
A
ˆ
Z
B
ˆ
∙
X
A
ˆ
X
B
ˆ
∙
Y
A
ˆ
Y
B
ˆ
∙
Y
A
ˆ
Y
B
ˆ
∙
Y
A
ˆ
X
B
ˆ
∙
Z
A
ˆ
Y
B
ˆ
∙
Z
A
ˆ
Z
B
ˆ
∙
Z
A
ˆ
]
_{B}^{A}R = ( ^{A}\^{X_{B}} ^{A}\^{Y_{B}} ^{A}\^{Z_{B}} ) = \left[ \begin{array}{ccc} \^{X_{B}} ∙ \^{X_{A}} & \^{Y_{B}} ∙ \^{X_{A}} & \^{Z_{B}} ∙ \^{X_{A}}\\ \^{X_{B}} ∙ \^{Y_{A}} & \^{Y_{B}} ∙ \^{Y_{A}}& \^{Y_{B}} ∙ \^{Y_{A}}\\ \^{X_{B}} ∙ \^{Z_{A}} & \^{Y_{B}} ∙ \^{Z_{A}} & \^{Z_{B}} ∙ \^{Z_{A}} \end{array} \right ]
BAR=(AXBˆAYBˆAZBˆ)=
XBˆ∙XAˆXBˆ∙YAˆXBˆ∙ZAˆYBˆ∙XAˆYBˆ∙YAˆYBˆ∙ZAˆZBˆ∙XAˆYBˆ∙YAˆZBˆ∙ZAˆ
按照刚刚我们理解的矩阵的本质, X A ˆ \^{X_{A}} XAˆ 被矩阵映射后,变成单位向量 X B ˆ \^{X_{B}} XBˆ 在 X A ˆ 、 Y A ˆ 、 Z A ˆ \^{X_{A}}、\^{Y_{A}}、\^{Z_{A}} XAˆ、YAˆ、ZAˆ 三个基向量上的投影,合成后刚刚好是 X B ˆ \^{X_{B}} XBˆ; Y A ˆ \^{Y_{A}} YAˆ 被矩阵映射后,变成单位向量 Y B ˆ \^{Y_{B}} YBˆ 在 X A ˆ 、 Y A ˆ 、 Z A ˆ \^{X_{A}}、\^{Y_{A}}、\^{Z_{A}} XAˆ、YAˆ、ZAˆ 三个基向量上的投影,合成后刚刚好是 Y B ˆ \^{Y_{B}} YBˆ; Z A ˆ \^{Z_{A}} ZAˆ 被矩阵映射后,变成单位向量 Z B ˆ \^{Z_{B}} ZBˆ 在 X A ˆ 、 Y A ˆ 、 Z A ˆ \^{X_{A}}、\^{Y_{A}}、\^{Z_{A}} XAˆ、YAˆ、ZAˆ 三个基向量上的投影,合成后刚刚好是 Z B ˆ \^{Z_{B}} ZBˆ,这个旋转矩阵其实就是对坐标系 A {A} A 的空间变换,形成了坐标系 B {B} B
有了
B
{B}
B 坐标系的姿态,现在我们要还需要一个位矢
A
P
B
O
R
G
^{A}{P_{BORG}}
APBORG 来确定
B
{B}
B 坐标系相对于
A
{A}
A 坐标系的相对位置,最终可以将
B
{B}
B 坐标系的姿态表达为
B
=
B
A
R
,
A
P
B
O
R
G
{B} = {{_{B}^{A}R, ^{A}{P_{BORG}}}}
B=BAR,APBORG
学习完三维空间中的两个坐标系的位姿表达后,我们来讨论坐标系
A
{A}
A 中的一个位矢如何在坐标系
B
{B}
B 中表达出来,我们先在两个坐标系的原点重合的情况下讨论,假设坐标系
A
{A}
A 中有个位矢
P
P
P,根据矩阵的映射原理可得,位矢
P
P
P 在坐标系
A
{A}
A 中的表达等价于位矢
P
P
P 在坐标系
B
{B}
B 中的表达再从坐标系
B
{B}
B 映射到坐标系
A
{A}
A
A
P
=
B
P
B
A
R
^{A}P = ^{B}P_ {B}^{A}R
AP=BPBAR

如果两个坐标系的原点不重合,我们还要考虑两个坐标系原点的位矢 A P B O R G ^{A}{P_{BORG}} APBORG ,位矢 A P B O R G ^{A}{P_{BORG}} APBORG 是以坐标系 A {A} A 为参照给出来的,所以不需要进行坐标系映射,直接进行矢量加和即可
A
P
=
B
P
B
A
R
+
A
P
B
O
R
G
^{A}P = ^{B}P_ {B}^{A}R + ^{A}{P_{BORG}}
AP=BPBAR+APBORG
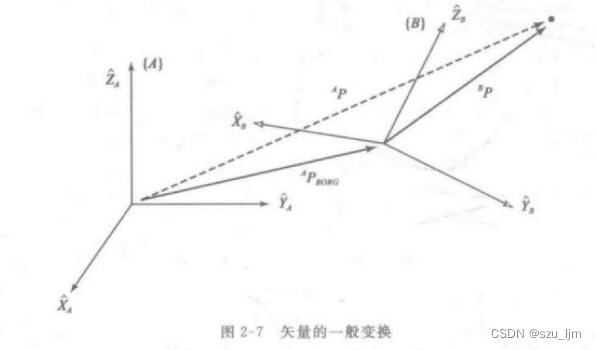
下面我们引入一个4x4的齐次变换矩阵来替换上面的式子,这样子表达更加明确简洁
[
A
P
1
]
=
[
B
A
R
A
P
B
O
R
G
[
0
0
0
]
1
]
[
B
P
1
]
\left[ \begin{array}{ccc} ^{A}P\\ 1\\ \end{array} \right ] = \left[ \begin{array}{ccc} _ {B}^{A}R & ^{A}{P_{BORG}}\\ \left[ \begin{array}{ccc} 0& 0 & 0\\ \end{array} \right ] & 1\\ \end{array} \right ]\left[ \begin{array}{ccc} ^{B}P \\ 1 \end{array} \right ]
[AP1]=[BAR[000]APBORG1][BP1]
2. 欧拉角与四元数
试着想象一架飞机,在飞机质心处有一个坐标系 B {B} B,坐标系 B {B} B 绕它的 Z Z Z 轴旋转 α \alpha α 角,再绕它的 Y Y Y 轴旋转 β \beta β 角,最后绕它的 X X X 轴旋转 γ \gamma γ 角,这一组旋转三个角的集合被称为欧拉角。欧拉角有三个分别为yaw(偏航角)、pitch(俯仰角)、roll(翻滚角),代表着绕着Z/Y/X轴旋转的角度
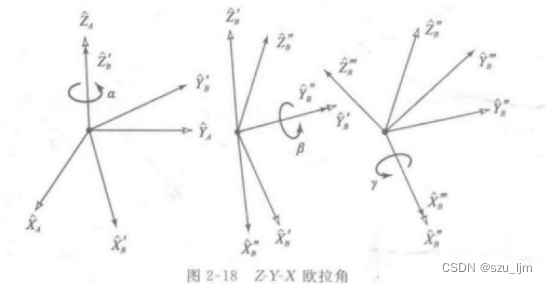
按照上面欧拉角形成的过程,我们结合旋转矩阵的原理可以给出每次旋转的数学表达式
R
Z
(
α
)
=
[
c
o
s
(
α
)
−
s
i
n
(
α
)
0
s
i
n
(
α
)
c
o
s
(
α
)
0
0
0
1
]
R_{Z}(\alpha) = \left[ \begin{array}{ccc} cos(\alpha) & -sin(\alpha) & 0\\ sin(\alpha) & cos(\alpha)& 0\\ 0 &0 & 1 \end{array} \right ]
RZ(α)=
cos(α)sin(α)0−sin(α)cos(α)0001
R
Y
(
β
)
=
[
c
o
s
(
β
)
0
s
i
n
(
β
)
0
1
0
−
s
i
n
(
β
)
0
c
o
s
(
β
)
]
R_{Y}(\beta) = \left[ \begin{array}{ccc} cos(\beta) & 0 & sin(\beta)\\ 0 & 1& 0\\ -sin(\beta) &0 & cos(\beta) \end{array} \right ]
RY(β)=
cos(β)0−sin(β)010sin(β)0cos(β)
R
X
(
γ
)
=
[
1
0
0
0
c
o
s
(
γ
)
−
s
i
n
(
γ
)
0
s
i
n
(
γ
)
c
o
s
(
γ
)
]
R_{X}(\gamma) = \left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & cos(\gamma)& -sin(\gamma)\\ 0 &sin(\gamma) & cos(\gamma) \end{array} \right ]
RX(γ)=
1000cos(γ)sin(γ)0−sin(γ)cos(γ)
最后我们整合三个旋转矩阵的乘积就可以得到坐标系
B
{B}
B 在经过一组旋转后的形成的新的坐标系
B
′
{B^{'}}
B′ 的相关参数,我们用一个旋转矩阵
B
′
B
R
^{B}_{B^{'}}R
B′BR 来表达坐标系
B
{B}
B 到坐标系
B
′
{B^{'}}
B′ 映射关系
B
′
B
R
Z
−
Y
−
X
(
α
,
β
,
γ
)
=
[
c
o
s
(
α
)
c
o
s
(
β
)
c
o
s
(
α
)
s
i
n
(
β
)
s
i
n
(
γ
)
−
s
i
n
(
α
)
c
o
s
(
γ
)
c
o
s
(
α
)
s
i
n
(
β
)
c
o
s
(
γ
)
+
s
i
n
(
α
)
s
i
n
(
γ
)
s
i
n
(
α
)
c
o
s
(
β
)
s
i
n
(
α
)
s
i
n
(
β
)
s
i
n
(
γ
)
+
c
o
s
(
α
)
c
o
s
(
γ
)
s
i
n
(
α
)
s
i
n
(
β
)
c
o
s
(
γ
)
−
c
o
s
(
α
)
s
i
n
(
γ
)
−
s
i
n
(
β
)
c
o
s
(
β
)
s
i
n
(
γ
)
c
o
s
(
β
)
c
o
s
(
γ
)
]
^{B}_{B^{'}}R_{Z-Y-X} (\alpha,\beta,\gamma )= \left[ \begin{array}{ccc} cos(\alpha)cos(\beta) & cos(\alpha)sin(\beta)sin(\gamma)-sin(\alpha)cos(\gamma) & cos(\alpha)sin(\beta)cos(\gamma)+sin(\alpha)sin(\gamma)\\ sin(\alpha)cos(\beta) & sin(\alpha)sin(\beta)sin(\gamma)+cos(\alpha)cos(\gamma)& sin(\alpha)sin(\beta)cos(\gamma)-cos(\alpha)sin(\gamma)\\ -sin(\beta) &cos(\beta)sin(\gamma) & cos(\beta)cos(\gamma) \end{array} \right ]
B′BRZ−Y−X(α,β,γ)=
cos(α)cos(β)sin(α)cos(β)−sin(β)cos(α)sin(β)sin(γ)−sin(α)cos(γ)sin(α)sin(β)sin(γ)+cos(α)cos(γ)cos(β)sin(γ)cos(α)sin(β)cos(γ)+sin(α)sin(γ)sin(α)sin(β)cos(γ)−cos(α)sin(γ)cos(β)cos(γ)
四元数与复数类似,四元数其实就是对于基
(
a
,
i
⃗
,
j
⃗
,
k
⃗
)
{(a,\vec{i},\vec{j},\vec{k})}
(a,i,j,k) 的线性组合,是由一个标量和一个3x1的矢量组成,我们以复数类比四元数,四元数的标量就是复数的实部,四元数的矢量就是复数的虚部
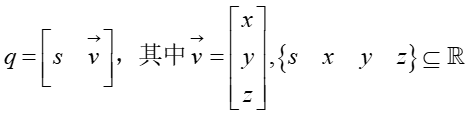
四元数的乘法遵循下面的性质,自身相乘就是-1,和其他相乘与叉乘的性质一样,遵循右手定则
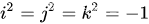
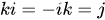
我们定义
q
\mathbf{q}
q 是一个单位四元数,又可将其表达为
q
=
w
+
x
i
+
y
j
+
z
k
\mathbf{q} = w +xi +yj+zk
q=w+xi+yj+zk,由于
q
\mathbf{q}
q 是一个单位四元数
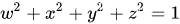
四元数
q
\mathbf{q}
q 的旋转矩阵
R
q
\mathbf{R}_{\mathbf{q}}
Rq 可以表达为
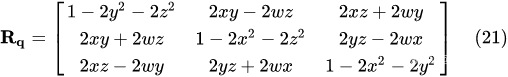
二、ROS中python实现坐标变换
1. 坐标msg消息载体
订阅发布模型中数据载体 msg 是一个重要实现环节,在坐标转换实现中常用的坐标数据消息载体msg有geometry_msgs/TransformStamped和geometry_msgs/PointStamped
下面是geometry_msgs/TransformStamped消息返回后的一些数据,我们就可以得到两个坐标系之间的位姿关系,一般这里的父级坐标系我们选择世界坐标系"world"
std_msgs/Header header #头信息
uint32 seq #|-- 序列号
time stamp #|-- 时间戳
string frame_id #|-- 坐标 ID
string child_frame_id #子坐标系的 id
geometry_msgs/Transform transform #坐标信息
geometry_msgs/Vector3 translation #偏移量
float64 x #|-- X 方向的偏移量
float64 y #|-- Y 方向的偏移量
float64 z #|-- Z 方向上的偏移量
geometry_msgs/Quaternion rotation #四元数
float64 x
float64 y
float64 z
float64 w
下面是geometry_msgs/PointStamped消息返回后的一些数据,我们就可以确定该点在所属坐标系的位置
std_msgs/Header header #头信息
uint32 seq #|-- 序号
time stamp #|-- 时间戳
string frame_id #|-- 所属坐标系的 id
geometry_msgs/Point point #点坐标
float64 x #|-- x y z 坐标
float64 y
float64 z
有了这些消息数据,我们就能实现一些好玩强大的功能,比如仿真环境中的乌龟跟随
2. 乌龟跟随的程序实现
乌龟跟随实现的核心,是乌龟A和B都要发布相对世界坐标系的坐标信息,然后订阅到该信息需要转换获取A相对于B坐标系的信息,最后生成线速度和角速度信息,并控制乌龟B运动。
首先在工作空间的src目录下,选择Create Catkin Package选项新建一个功能包,添加 tf2、tf2_ros、tf2_geometry_msgs、roscpp rospy std_msgs等依赖包,接着新建scripts文件夹用于存放python文件,创建launch文件夹用于存放launch文件
首先我们调用ROS的服务生成第二只小乌龟,创建第二只乌龟需要使用rosservice,话题使用的是 /spawn
#! /usr/bin/env python
#1.导包
import rospy
from turtlesim.srv import Spawn, SpawnRequest, SpawnResponse
if __name__ == "__main__":
# 2.初始化 ros 节点
rospy.init_node("turtle_spawn_p")
# 3.创建服务客户端
client = rospy.ServiceProxy("/spawn",Spawn)
# 4.等待服务启动
client.wait_for_service()
# 5.创建请求数据
req = SpawnRequest()
req.x = 1.0
req.y = 1.0
req.theta = 0
req.name = "turtle2"
# 6.发送请求并处理响应
try:
response = client.call(req)
rospy.loginfo("乌龟创建成功,名字是:%s",response.name)
except Exception as e:
rospy.loginfo("服务调用失败....")
接着我们需要编写坐标消息话题发布节点,我们通过话题 / 乌龟名称 / p o s e /乌龟名称/pose /乌龟名称/pose 来获取乌龟位姿,并将其解算成相对世界坐标系的坐标消息,然后发布出去
#! /usr/bin/env python
# 1.导包
import rospy
import sys
from turtlesim.msg import Pose
from geometry_msgs.msg import TransformStamped
import tf2_ros
import tf_conversions
turtle_name = ""
def doPose(pose):
# rospy.loginfo("x = %.2f",pose.x)
#1.创建坐标系广播器
broadcaster = tf2_ros.TransformBroadcaster()
#2.将 pose 信息转换成 TransFormStamped
tfs = TransformStamped()
tfs.header.frame_id = "world"
tfs.header.stamp = rospy.Time.now()
tfs.child_frame_id = turtle_name
tfs.transform.translation.x = pose.x
tfs.transform.translation.y = pose.y
tfs.transform.translation.z = 0.0
qtn = tf_conversions.transformations.quaternion_from_euler(0, 0, pose.theta)
tfs.transform.rotation.x = qtn[0]
tfs.transform.rotation.y = qtn[1]
tfs.transform.rotation.z = qtn[2]
tfs.transform.rotation.w = qtn[3]
#3.广播器发布 tfs
broadcaster.sendTransform(tfs)
if __name__ == "__main__":
# 2.初始化 ros 节点
rospy.init_node("sub_tfs_p")
# 3.解析传入的命名空间
rospy.loginfo("-------------------------------%d",len(sys.argv))
if len(sys.argv) < 2:
rospy.loginfo("请传入参数:乌龟的命名空间")
else:
turtle_name = sys.argv[1]
rospy.loginfo("///乌龟:%s",turtle_name)
rospy.Subscriber(turtle_name + "/pose",Pose,doPose)
# 4.创建订阅对象
# 5.回调函数处理订阅的 pose 信息
# 5-1.创建 TF 广播器
# 5-2.将 pose 信息转换成 TransFormStamped
# 5-3.发布
# 6.spin
rospy.spin()
最后我们需要编写坐标消息话题订阅节点,通过订阅 turtle1 和 turtle2 的 TF坐标 广播信息,查找并转换时间最近的 TF坐标 信息将 turtle1 转换成相对 turtle2 的坐标,再计算线速度和角速度并发布到乌龟运动控制话题
#! /usr/bin/env python
# 1.导包
import rospy
import tf2_ros
from geometry_msgs.msg import TransformStamped, Twist
import math
if __name__ == "__main__":
# 2.初始化 ros 节点
rospy.init_node("sub_tfs_p")
# 3.创建 TF 订阅对象
buffer = tf2_ros.Buffer()
listener = tf2_ros.TransformListener(buffer)
# 4.处理订阅到的 TF
rate = rospy.Rate(10)
# 创建速度发布对象
pub = rospy.Publisher("/turtle2/cmd_vel",Twist,queue_size=1000)
while not rospy.is_shutdown():
rate.sleep()
try:
#def lookup_transform(self, target_frame, source_frame, time, timeout=rospy.Duration(0.0)):
trans = buffer.lookup_transform("turtle2","turtle1",rospy.Time(0))
# rospy.loginfo("相对坐标:(%.2f,%.2f,%.2f)",
# trans.transform.translation.x,
# trans.transform.translation.y,
# trans.transform.translation.z
# )
# 根据转变后的坐标计算出速度和角速度信息
twist = Twist()
# 间距 = x^2 + y^2 然后开方
twist.linear.x = 0.5 * math.sqrt(math.pow(trans.transform.translation.x,2) + math.pow(trans.transform.translation.y,2))
twist.angular.z = 4 * math.atan2(trans.transform.translation.y, trans.transform.translation.x)
pub.publish(twist)
except Exception as e:
rospy.logwarn("警告:%s",e)
在终端里给python文件添加可执行权限
chmod +777 *.py
按照上次笔记的方法配置好CMakeLists.txt文件,将要编译三个.py文件声明一下,然后catkin_make:build编译后看看有没有报错,没有报错就可以编写launch文件
<launch>
<node pkg="turtlesim" type="turtlesim_node" name="turtle1" output="screen" />
<node pkg="turtlesim" type="turtle_teleop_key" name="key_control" output="screen"/>
<node pkg="xxx" type="xxx.py" name="turtle_spawn" output="screen"/>
<node pkg="xxx" type="xxx.py" name="tf_pub1" args="turtle1" output="screen"/>
<node pkg="xxx" type="xxx.py" name="tf_pub2" args="turtle2" output="screen"/>
<node pkg="xxx" type="xxx.py" name="tf_sub" output="screen"/>
</launch>
编写好launch文件后右键launch文件打开终端运行launch文件就可以看见乌龟跟随效果
roslaunch xxx(功能包) xxx.launch(launch文件)
总结
以上就是机器人坐标变换的学习笔记,本片笔记简单地介绍了机器人坐标变换的理论基础和ROS中的TF坐标变换实现过程。机器人坐标变换的重要性在于它可以使机器人在不同坐标系下保持一致的运动精度。因为在不同的坐标系下,机器人的运动轨迹和位置信息都会发生变化。例如,机器人在基座坐标系下的运动可能是直线运动,但在工具坐标系下的运动可能是旋转运动。如果不进行坐标变换,机器人的运动轨迹和位置信息就会出现偏差,导致机器人无法精确地完成任务。