1 Introduction

1.1 Policy-Based Reinforcement Learning

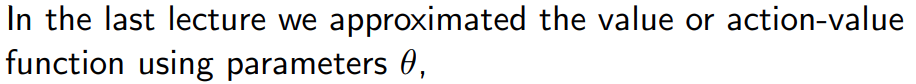
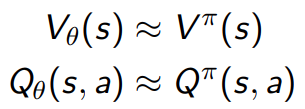
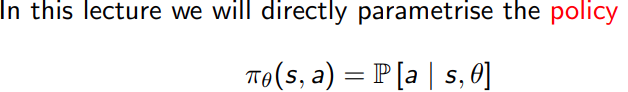
1.2 Value-based and policy based RL

基于值的强化学习
在基于值的 RL 中，目标是找到一个最优的值函数，通常是 Q 函数或 V 函数。这些函数为给定的状态或状态-动作对分配一个值，表示从该状态开始或在该状态下执行特定动作的预期回报。通过这种方式，智能体可以选择那些具有最高值的动作。

Q-Learning 和 Deep Q Network (DQN) 就是基于值的 RL 的例子。这些方法都试图优化 Q 函数，从而间接地优化策略。

基于策略的强化学习
在基于策略的 RL 中，目标是直接找到最优策略，无需通过值函数。这通常通过参数化策略并使用优化算法（如梯度上升）来最大化预期回报来实现。
基于策略的方法可以处理连续的、高维的动作空间，这在基于值的方法中往往很难处理。Policy Gradient 和 Actor-Critic 是基于策略的 RL 的例子。

区别和联系
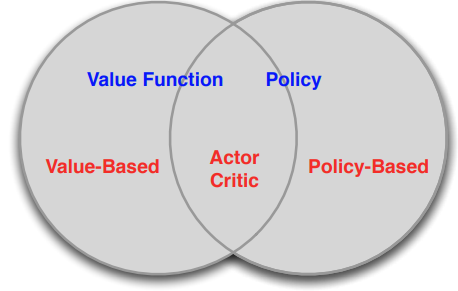
基于值的 RL 和基于策略的 RL 的主要区别在于，前者通过优化值函数间接优化策略，而后者直接优化策略。
然而，这两种类型的 RL 也可以结合在一起，形成所谓的 Actor-Critic 方法。在这种方法中，策略（Actor）和值函数（Critic）都是显式表示的，而且都在学习过程中更新。Critic 评估 Actor 的策略性能，而 Actor 根据 Critic 的反馈来更新策略。这种方法结合了基于值和基于策略的 RL 的优点。

我们之前接触到的mento carlo和sarsa($\lambda$)都属于value based RL.

• Policy based RL
  

1.3 examples

• rock-paper-scissors game
  
• alias gridworld game
  
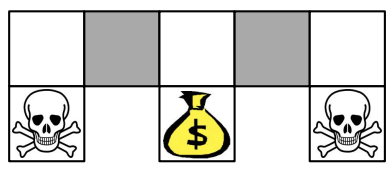
  对于没有全局定位的机器人来说，两种灰色的状态是类似的，alias state
  

value based RL 的值函数为每个状态-动作对分配一个值。然而，在这两个别名化的状态中，智能体应该采取不同的行动，但由于状态看起来是相同的，智能体会将同一个值分配给这两个状态，这导致智能体无法正确行动。

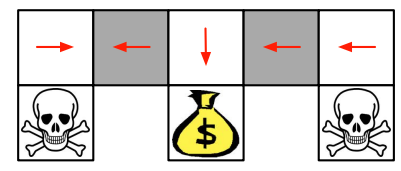
举例来说，对于右侧grey state，应该向左移动，但是对于左侧的grey state如果还往左移动就出错了。这就是value based RL的最大局限性。

采用policy based RL

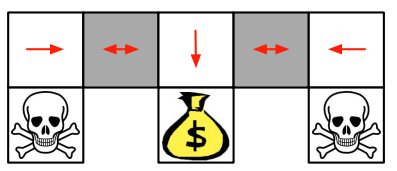
在灰色状态的时候，采用随机概率，就可能能达到最终目标。

1.4 Policy Search

看一个cartpole的问题，试图控制一个小车，使其上方的倒立杆保持直立。如果杆开始倾斜，我们需要移动小车以防止杆倒下。问题的目标是使杆尽可能长时间地保持直立。
这个问题的状态是一个四维向量，包含小车的位置、小车的速度、杆的角度和杆的角速度。每一步，我们可以选择两个动作之一：向左或向右推小车。
在策略梯度中，我们直接优化参数化的策略以获取更多的奖励。这是通过在每个时间步中对策略的参数应用梯度上升来完成的，其中梯度是奖励信号的函数。

代码的整体思路：通过收集到的经验(奖励和行为)来改进策略。

这是通过计算策略梯度并使用优化器对策略进行梯度上升来实现的。这个过程的背后有一个关键的概念：我们想要增加我们得到好奖励的动作的概率，减少我们得到坏奖励的动作的概率。
在函数中，首先初始化一个总回报R为0，并创建一个空的策略损失列表。然后我们遍历所有的奖励（从最后一步开始反向遍历），对每一步计算一个折扣回报R，并将这个回报乘以那一步的动作的负log概率。这个值被加入到策略损失列表中。这个过程实际上就是在计算策略梯度的公式：
策略梯度方法中，我们使用参数化的策略 πθ，其中 θ 是神经网络的参数。我们希望找到一组参数 θ，使得在这个策略下，累积回报的期望值最大。πθ，其中 θ 是神经网络的参数。
在训练过程中，我们基于已经采取的动作和得到的回报计算策略梯度，然后使用这个梯度来更新神经网络的参数。具体来说，我们计算每一步的策略梯度为 ${\nabla }_{\theta }log{\pi }_{\theta }(a_t|s_t)G_t$，然后将所有步骤的策略梯度加起来作为整个轨迹的策略梯度。这就相当于计算了一个误差信号，这个误差信号表示在当前策略下，如何改变参数 θ 才能使得回报的期望值增大。
在策略梯度中，我们定义的“损失函数”实际上是一个优化目标，这个目标是基于经验回报的。具体来说，我们使用的损失是 $-log{\pi }_{\theta }(a_t|s_t)G_t$，其中 Gt 是从时间步 t 到轨迹结束的累积回报，${\pi }_{\theta }(a_t|s_t)$ 是在状态 st 下采取动作 at 的概率，负号表示我们希望最大化这个量（因为优化算法通常是最小化损失函数）。$-log{\pi }_{\theta }(a_t|s_t)G_t$，其中 Gt 是从时间步 t 到轨迹结束的累积回报，${\pi }_{\theta }(a_t|s_t)$ 是在状态 st 下采取动作 $-log{\pi }_{\theta }(a_t|s_t)G_t$
这样定义损失函数的原因是，我们希望在策略产生好的结果（高回报）时，增加导致这个结果的动作的概率；反之，如果策略产生的结果不好（低回报），我们希望降低导致这个结果的动作的概率。而 $-log{\pi }_{\theta }(a_t|s_t)G_t$这个量的梯度正好满足这个需求

import gym
import torch
import torch.nn as nn
import torch.optim as optim

class Policy(nn.Module):
    def __init__(self):
        super(Policy, self).__init__()
        self.affine1 = nn.Linear(4, 128)
        self.dropout = nn.Dropout(p=0.6)
        self.affine2 = nn.Linear(128, 2)

    def forward(self, x):
        x = self.affine1(x)
        x = self.dropout(x)
        x = torch.relu(x)
        action_scores = self.affine2(x)
        return torch.softmax(action_scores, dim=1)

def select_action(policy, state):
    state = torch.from_numpy(state).float().unsqueeze(0)
    probs = policy(state)
    m = torch.distributions.Categorical(probs)
    action = m.sample()
    return action.item(), m.log_prob(action)

def train(policy, optimizer, rewards, log_probs):
    R = 0
    policy_loss = []
    for r in rewards[::-1]:
        R = r + 0.99 * R
        policy_loss.append(-log_prob * R)
    optimizer.zero_grad()
    policy_loss = torch.cat(policy_loss).sum()
    policy_loss.backward()
    optimizer.step()

def main():
    env = gym.make('CartPole-v0')
    policy = Policy()
    optimizer = optim.Adam(policy.parameters(), lr=1e-2)
    for i_episode in range(1000):
        state = env.reset()
        rewards = []
        log_probs = []
        for t in range(10000):  # Don't infinite loop while learning
            action, log_prob = select_action(policy, state)
            state, reward, done, _ = env.step(action)
            rewards.append(reward)
            log_probs.append(log_prob)
            if done:
                break

        train(policy, optimizer, rewards, log_probs)

    env.close()

if __name__ == '__main__':
    main()

1.4.1 policy objective functions

policy objective functions:

• 收集数据
  
• 优化模型
  

2 Finite Difference policy Gradient

2.1 Policy Gradient

通过policy gradient 方法进行数值迭代

通过数值差分的方法，计算gradient进行优化

对于刚才那个神经网络的问题，定义loss function，进行神经网络的训练。

2.2 AIBO example

2.3 Likelihood Ratios

• score function
  通过似然比技巧，将策略梯度的表达式转换成更容易处理的形式。由技巧
  $${\Delta }_{\theta }f(x)=f(x)\ast {\Delta }_{\theta }log(f(x))$$
  可以得到转换后的policy gradient
  
  在我们刚才那个例子中，通过pytorch的log_prob来实现

def select_action(policy, state):
    state = torch.from_numpy(state).float().unsqueeze(0)
    probs = policy(state)
    m = torch.distributions.Categorical(probs)
    action = m.sample()
    return action.item(), m.log_prob(action)

• softmax policy
  我们首先定义动作的概率分布为softmax函数的形式。假设我们有动作值函数 Q(s,a;θ)，对于状态 s 和动作 a，动作概率被定义为
  $$\pi (a|s;\theta )=\frac{exp(Q(s,a;\theta ))}{{\sum }_{a^{\prime }}exp(Q(s,a^{\prime };\theta ))}$$
  在这种情况下，策略梯度定理会稍微变形。在softmax策略下，策略梯度的形式为：
  $${\Delta }_{\theta }J(\theta )=E_{\pi }[{\Delta }_{\theta }log\pi (a|s;\theta )\ast Q^{\pi }(s,a)]$$
  得到score function是：
  

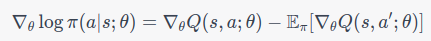
根据GPT给出的推导的过程：

然而，这个形式在实践中并不好计算，因为计算动作值函数 Qπ(s,a) 通常是困难的。因此，我们通常使用一个称为优势函数的替代项：
$$A^{\pi }(s,a)=Q^{\pi }(s,a)-V^{\pi }(s)$$

这里的 Vπ(s) 是状态值函数。优势函数表示选择动作 a 而不是平均情况下的预期回报。因此，策略梯度定理在实践中常常被写为：Vπ(s) 是状态值函数。优势函数表示选择动作 a 而不是平均情况下的预期回报
$${\Delta }_{\pi }J(\theta )=E_{\pi }[{\Delta }_{\theta }log\pi (a|s;\theta )\ast A^{\pi }(s,a)]$$

对于线性feature $\varphi (s,a{)}^T\theta$, 根据score function的公式，可以得到下面的结论

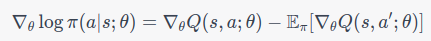
• Gaussian policy
  
  推导过程如下：
  
  

2.4 policy gradient theorem

• one-step MDPs
  
  
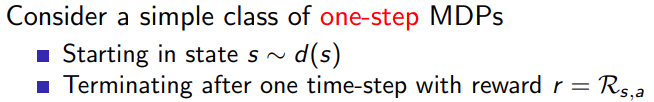
  替换公式中的瞬时reward到long-term value $Q^{\pi }(s,a)$
  
  作用
  

在某些强化学习算法中，会同时训练两个网络，一个用来近似价值函数（通常是动作价值函数Q(s,a)），另一个用来近似策略函数。这种方法通常被称为Actor-Critic方法。Q(s,a)），另一个用来近似策略函数。这种方法通常被称为Actor-Critic方法
在Actor-Critic方法中，“Actor”部分是用来近似策略函数的网络，它根据当前状态s选择动作a；而“Critic”部分是用来近似价值函数的网络，它评估在给定状态s下采取动作a的预期回报。"Critic"通过计算TD-error来更新价值函数，而"Actor"则通过使用策略梯度方法（如您之前提到的$Q^{\pi }(s,a)$）来更新策略函数。s选择动作a；而“Critic”部分是用来近似价值函数的网络，它评估在给定状态s下采取动作a的预期回报。"Critic"通过计算TD-error来更新价值函数，而"Actor"则通过使用策略s选择动作a；而“Critic”部分是用来近似价值函数的网络，它评估在给
Actor-Critic方法确实可以说是混合了value based和policy based的RL方法，因为它同时使用了价值函数和策略函数。这种方法的优点在于，它可以利用价值函数的稳定性和策略函数的灵活性，从而在强化学习任务中实现更好的性能。

3 Monte Carlo Policy Gradient

3.1 mente-carlo policy gradient

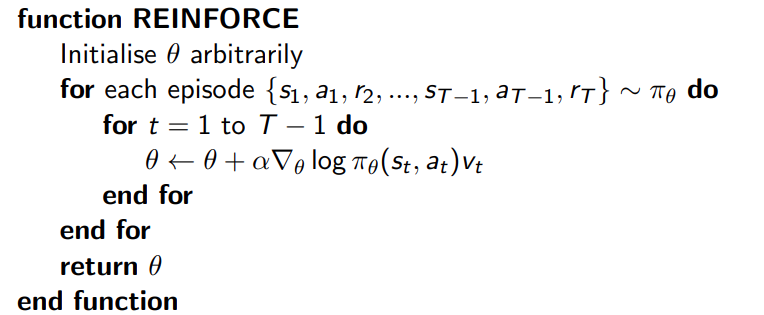
import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim

class PolicyNetwork(nn.Module):
    def __init__(self, n_inputs, n_outputs):
        super(PolicyNetwork, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(n_inputs, 64),
            nn.ReLU(),
            nn.Linear(64, n_outputs),
            nn.Softmax(dim=-1)
        )

    def forward(self, x):
        return self.model(x)

def train(env, policy, optimizer, gamma=0.99, max_episodes=1000):
    for episode in range(max_episodes):
        state = env.reset()
        log_probs = []
        rewards = []

        # Generate an episode
        done = False
        while not done:
            state = torch.FloatTensor(state)
            action_probs = policy(state)
            action_dist = torch.distributions.Categorical(action_probs)
            action = action_dist.sample()
            log_prob = action_dist.log_prob(action)
            state, reward, done, _ = env.step(action.item())

            log_probs.append(log_prob)
            rewards.append(reward)

        # Compute discounted returns
        returns = []
        R = 0
        for r in rewards[::-1]:
            R = r + gamma * R
            returns.insert(0, R)
        returns = torch.tensor(returns)
        returns = (returns - returns.mean()) / (returns.std() + 1e-5)

        # Compute policy gradient
        policy_loss = []
        for log_prob, R in zip(log_probs, returns):
            policy_loss.append(-log_prob * R)
        policy_loss = torch.cat(policy_loss).sum()

        # Update policy
        optimizer.zero_grad()
        policy_loss.backward()
        optimizer.step()

        if episode % 100 == 0:
            print('Episode {}\tLoss: {:.2f}'.format(episode, policy_loss.item()))

def main():
    env = gym.make('CartPole-v0')
    policy = PolicyNetwork(env.observation_space.shape[0], env.action_space.n)
    optimizer = optim.Adam(policy.parameters(), lr=1e-2)
    train(env, policy, optimizer)

if __name__ == '__main__':
    main()

4 Actor Critic Policy Gradient

4.1 说明

• Reducing Variance using a Critic
  
• Estimating the action-value function
  
• Action-Value Actor-Critic
  

对于Actor-Critic方法，我们需要同时更新Actor和Critic。其中Actor负责选择动作，Critic负责评估当前状态-动作对的值。这个过程可以看作是一种动态的、交互式的过程，Actor基于Critic的反馈来更新自己的策略，而Critic则基于Actor的动作来更新状态-动作对的估计值。

在这个CartPole问题中，我们采用的Sarsa(λ)算法，它是一种时序差分学习方法，这意味着它在更新状态-动作对的值时，同时考虑了当前的奖励和下一个状态-动作对的估计值。

在代码中，每一个episode开始时，我们首先重置环境和资格迹。在每一步中，我们首先根据当前的状态选择一个动作，然后执行这个动作并观察环境的反馈。接着，我们计算TD误差，这是实际的奖励和我们的估计值之间的差距。然后，我们使用这个TD误差来更新Critic的参数。

对于Actor的更新，我们使用了策略梯度方法。这里的损失函数是-log(action_prob) * td_error，这实际上就是对策略梯度公式的一种实现。在计算损失函数后，我们使用反向传播来计算梯度，然后应用这个梯度来更新Actor的参数。

需要注意的是，在更新Actor的参数时，我们使用了资格迹。这是因为在Sarsa(λ)中，我们不仅考虑了当前的状态-动作对，还考虑了之前的状态-动作对。这样可以更好地将未来的奖励反向传播到之前的状态-动作对，从而提高学习效率。

在实际训练的过程中，通过储存replay buffer，复用过去的经验来更新网络。用这种方式sarsa(\lambda)也可以使用batch training的方法来更新q-table的网络和policy \theta的网络。
两者分别用value error和 policy gradient来更新网络。

import torch
import torch.nn as nn
import torch.optim as optim
import gym
import numpy as np
from collections import deque
import random

class Actor(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(Actor, self).__init__()
        self.linear1 = nn.Linear(input_dim, 128)
        self.linear2 = nn.Linear(128, output_dim)
        
    def forward(self, state):
        x = torch.relu(self.linear1(state))
        x = torch.softmax(self.linear2(x), dim=-1)
        return x

class Critic(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(Critic, self).__init__()
        self.linear1 = nn.Linear(input_dim, 128)
        self.linear2 = nn.Linear(128, output_dim)
        
    def forward(self, state):
        x = torch.relu(self.linear1(state))
        x = self.linear2(x)
        return x

class ActorCritic:
    def __init__(self, input_dim, action_dim, gamma=0.99):
        self.actor = Actor(input_dim, action_dim)
        self.critic = Critic(input_dim, 1)
        self.optimizer_actor = optim.Adam(self.actor.parameters())
        self.optimizer_critic = optim.Adam(self.critic.parameters())
        self.gamma = gamma
        self.replay_buffer = deque(maxlen=10000)

    def get_action(self, state):
        state = torch.tensor(state, dtype=torch.float).unsqueeze(0)
        probs = self.actor(state)
        action = np.random.choice(len(probs[0]), p=probs.detach().numpy()[0])
        return action

    def update(self, batch_size):
        if len(self.replay_buffer) < batch_size:
            return

        minibatch = random.sample(self.replay_buffer, batch_size)
        states, actions, rewards, next_states, dones = zip(*minibatch)
        states = torch.tensor(states, dtype=torch.float)
        actions = torch.tensor(actions, dtype=torch.long)
        rewards = torch.tensor(rewards, dtype=torch.float)
        next_states = torch.tensor(next_states, dtype=torch.float)
        dones = torch.tensor(dones, dtype=torch.float)

        Q_vals = self.critic(states).squeeze()
        next_Q_vals = self.critic(next_states).squeeze()
        Q_target = rewards + self.gamma * next_Q_vals * (1 - dones)

        # update critic
        loss_critic = nn.MSELoss()(Q_vals, Q_target.detach())
        self.optimizer_critic.zero_grad()
        loss_critic.backward()
        self.optimizer_critic.step()
		# update actor
        action_probs = self.actor(states)
        chosen_action_probs = action_probs.gather(1, actions.unsqueeze(1)).squeeze()
        loss_actor = -torch.sum(torch.log(chosen_action_probs) * Q_target.detach())

        self.optimizer_actor.zero_grad()
        loss_actor.backward()
        self.optimizer_actor.step()

    def store_transition(self, state, action, reward, next_state, done):
        self.replay_buffer.append((state, action, reward, next_state, done))

def main():
    env = gym.make("CartPole-v0")
    input_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n

    agent = ActorCritic(input_dim, action_dim)

    num_episodes = 500
    batch_size = 32

    for ep in range(num_episodes):
        state = env.reset()
        total_reward = 0
        done = False
        while not done:
            action = agent.get_action(state)
            next_state, reward, done, _ = env.step(action)
            agent.store_transition(state, action, reward, next_state, done)
            agent.update(batch_size)
            state = next_state
            total_reward += reward

        print(f"Episode {ep}, Reward: {total_reward}")

if __name__ == "__main__":
    main()

4.2 Compatible function Approximation

• bias in actor-critic algorithms
  
• Compatible Function Approximation
  
• Proof of Compatible Function Approximation Theorem

"Compatible Function Approximation"是一个在强化学习中用来确保策略梯度有一个良好性质的方法。这个性质就是当我们使用一个特定类型的值函数近似时（具体来说，这个值函数近似和我们的策略有一定的兼容性），策略梯度就是真实的策略梯度的一个无偏估计。这意味着在平均意义下，我们的策略梯度的估计是准确的。
这个方法的关键思想就是，我们的值函数近似（Q函数）应该和我们的策略有一定的兼容性。具体来说，我们的值函数近似的梯度应该与我们的策略的梯度有关。为了满足这个条件，我们使用以下的值函数近似：

策略网络和值函数网络往往是独立的，它们各自有自己的参数，它们的梯度不一定有任何直接的关系。但这并不妨碍我们使用"Compatible Function Approximation"的理论去指导我们的算法设计。
首先，需要明确的是，"Compatible Function Approximation"的理论并不一定需要在实际应用中严格遵守。这个理论是一个理想的情况，它给出了一个理想的值函数近似应该满足的性质。在实际应用中，我们可能无法（或者不需要）严格满足这些性质，但我们可以尽量接近它。
其次，尽管在实际应用中，我们的策略网络和值函数网络可能是独立的，但我们可以通过训练过程去使它们尽量接近"Compatible Function Approximation"的理论。具体来说，我们可以通过以下方式去做：

1. 我们可以通过优化目标函数去促使策略网络和值函数网络的梯度尽可能接近。具体来说，我们可以使用一个目标函数，它包含了策略网络和值函数网络的梯度的差的平方。这样，我们的优化过程就会尽量使得策略网络和值函数网络的梯度接近。
2. 我们可以在训练过程中共享一部分网络结构。具体来说，我们的策略网络和值函数网络可以共享一部分底层的网络结构，这样，它们的梯度就有可能更接近。

需要注意的是，这些都是尽量接近"Compatible Function Approximation"的理论的方法，它们并不能保证我们的策略网络和值函数网络的梯度完全一致。但在实际应用中，这些方法已经足够好了，它们可以使我们的训练过程更稳定，更容易收敛。

4.3 Advantage Function Critic

• Reducing Variance Using a Baseline
  
  Advantage Function的直观理解是，在状态s下采取动作a相比于在状态s下按照策略π采取动作的平均优势。
  减少方差：相比于使用原始的回报（reward-to-go）或者Q值，使用Advantage Function可以减少方差，使得学习过程更加稳定。因为Advantage Function已经减去了值函数V(s)，这相当于减去了一个基线（baseline），可以减少估计的方差。

更好的指导策略优化：Advantage Function可以更好地指导策略优化。因为Advantage Function表示的是采取某个动作相对于平均水平的优势，所以我们在优化策略的时候，应该更倾向于增加那些有正优势（positive advantage）的动作的概率，减少那些有负优势（negative advantage）的动作的概率。

有助于解决探索与利用的问题：通过使用Advantage Function，我们可以更好地平衡探索与利用的问题。因为Advantage Function可以指示我们哪些动作可能比平均水平更好，哪些动作可能比平均水平更差，这可以帮助我们在选择动作的时候，既考虑到利用已知的知识，也考虑到探索未知的动作。

4.3.1 estimating the advantage function

• 直接法
  计算advantage function，通过直接计算Q值和V值，然后相减。

• 通过TD间接计算

在实际应用中，我们确实需要计算动作值函数Q和状态值函数V来获取优势函数（Advantage Function）。然而，直接计算Q值和V值可能需要大量的样本和计算资源，因此在实践中，我们通常采用一些近似的方法。

一个常见的方法是使用Temporal Difference (TD) 学习的方法估计Advantage Function。这种方法不需要显式地计算Q值和V值，而是通过对即时奖励和未来奖励的估计进行比较来计算Advantage Function。具体来说，TD学习的优势函数可以通过以下公式进行定义：

A(s, a) = r(s, a) + γV(s’) - V(s)

其中，r(s, a)是采取动作a在状态s下获得的即时奖励，γ是折扣因子，V(s’)是在下一状态s’下的值函数估计，V(s)是在当前状态s下的值函数估计。

这种方法的好处是，它不需要显式地计算Q值，可以直接通过TD误差来估计Advantage Function，从而大大减少了计算和存储的需求。但是，它也有一个缺点，那就是它需要对环境的动态性有一个较好的估计，以便计算出准确的TD误差。

• 使用TD($\lambda$)计算advantage function.
  
  其中，α_w和α_θ分别是值函数和策略的学习率，γ是折扣因子，λ是资格迹参数，e是资格迹量。

这种方法的一个主要优点是，它可以利用资格迹量来有效地处理迟延奖励问题，即当奖励在时间步上被延迟时，通过保持一个资格迹量来“记住”过去的状态和动作，并利用这些信息来更新值函数和策略。

4.4 Eligibility Traces

4.4.1 Critic at different time-scale

另一个常见的方法是使用Actor-Critic方法来估计Advantage Function。在这种方法中，我们使用一个称为Actor的模型来估计策略，使用另一个称为Critic的模型来估计值函数。通过这种方式，我们可以在每个时间步中同时更新策略和值函数，从而更准确地估计Advantage Function。

4.4.2 actors at Different Time-scales

4.4.3 policy gradient with eligibility traces

4.5 Natural Policy Gradient

4.5.1 Alternative Policy Gradient Directions

Natural Policy Gradient是一种优化策略的方法，它是Policy Gradient的一种变体。它的主要思想是在优化策略时，不仅要考虑奖励的增加，还要考虑策略改变的大小，也就是说，它试图在保证策略改变不大的情况下，最大化奖励。为了衡量策略改变的大小，Natural Policy Gradient引入了一种名为Fisher信息度量的概念，它能够在某种意义上度量两个策略之间的距离。

具体来说，普通的Policy Gradient方法是基于梯度上升的思想来优化策略的，它每一步都沿着梯度的方向改变策略参数。然而，这种方法可能会导致策略改变过大，从而影响到学习的稳定性。相比之下，Natural Policy Gradient则是通过在优化过程中引入Fisher信息度量来限制策略改变的大小，从而提高了学习的稳定性。
Natural Policy Gradient的优点主要包括：

1.它能够提高学习的稳定性。通过限制策略改变的大小，它可以避免策略的过度更新，从而使学习过程更加稳定。

2.它能够更好地利用信息。由于它考虑了策略改变的大小，因此它能够在一定程度上利用更多的信息来优化策略。

Natural Policy Gradient主要适用于那些需要保持策略稳定性的场景，特别是在复杂的、连续的动作空间中，Natural Policy Gradient通常可以提供更好的性能。此外，由于它的优化过程涉及到Fisher信息度量的计算，因此它在计算资源有限的情况下也可能会表现得更好。

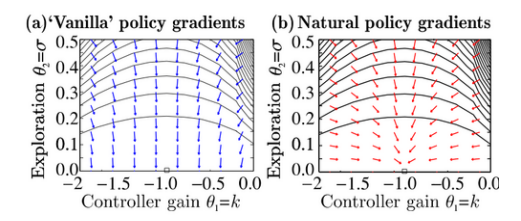
$G_{\theta }$ 是 Fisher Information Matrix，$G_{\theta }$^(-1) 是 $G_{\theta }$ 的逆矩阵。通过这种方式，NPG 能够考虑到参数空间的结构，从而使得更新步骤在所有方向上都更加均衡。

直观地说，标准的 Policy Gradient 方法可能会在参数空间的某些方向上更新过快，而忽略了其他方向。而 Natural Policy Gradient 方法则能够保证在所有方向上都有均匀的更新，从而使得学习过程更加稳定。

4.5.2 natural actor-critic

4.5.3 summary of policy Gradient Algorithms