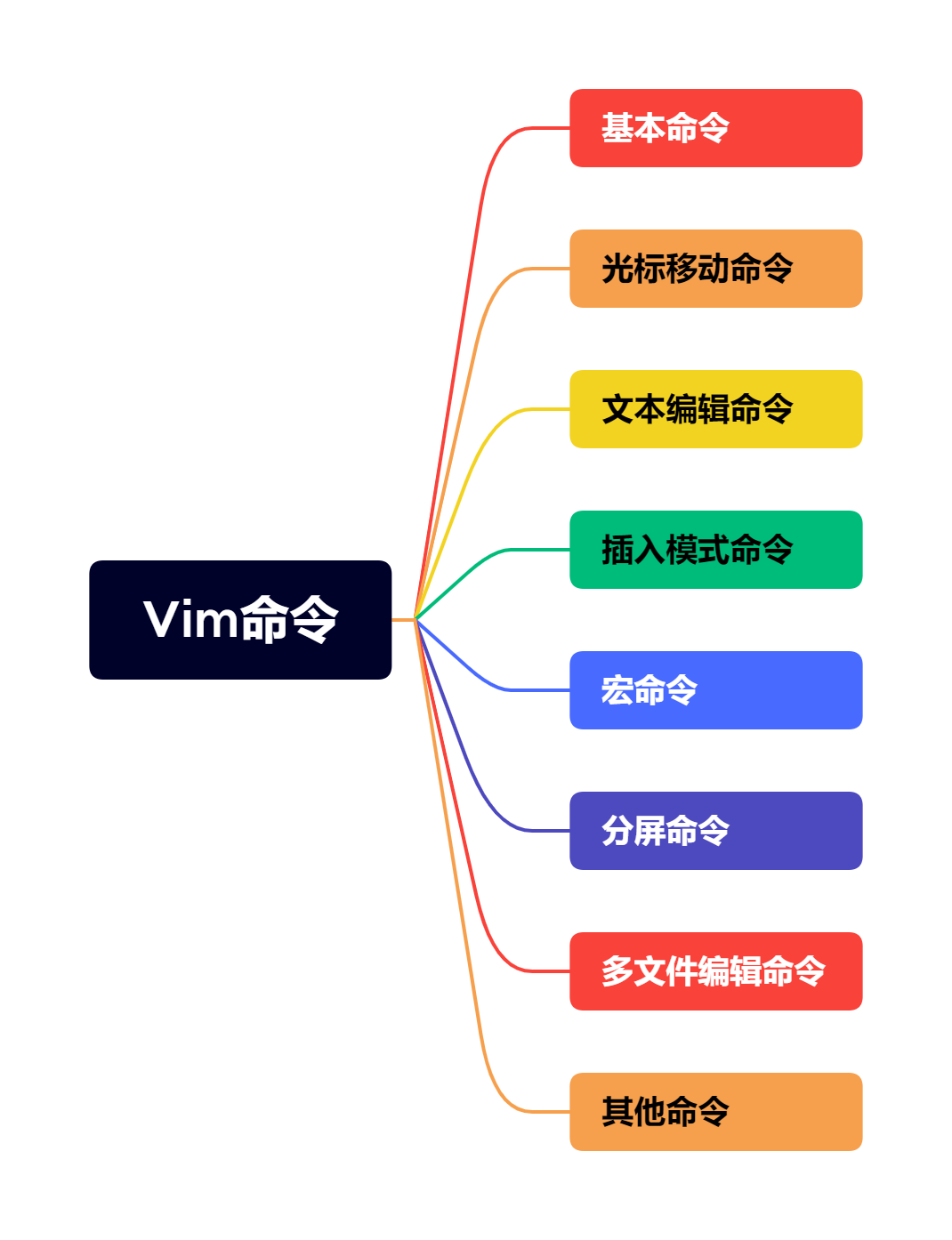
张量的谱表示

基于特征多项式：

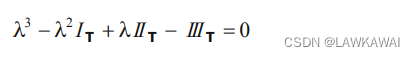
如果$T$ 是对称二阶张量，那么有三个实数特征值：$T_1,T_2,T_3$, 对应有特征向量：

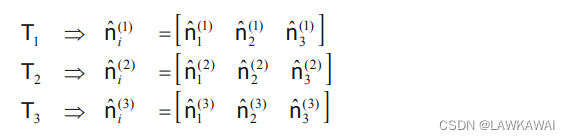
主空间由特征向量构成的正交基${\hat{n}}^{(1)},{\hat{n}}^{(2)},{\hat{n}}^{(3)}$ 所张成，张量的分量则由特征值表示：

特征向量形成的变换矩阵$A$:
$$T^{\prime }=AT{A}^{\prime }$$
由于$A^{-1}=A^T$， 所以：
$$T=A^T{T}^{\prime }A$$
其中：

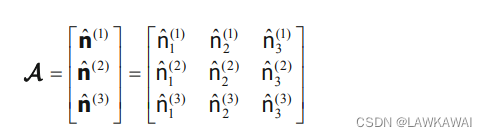
将$T=A^T{T}^{\prime }A$，显式表示出来：

其中：

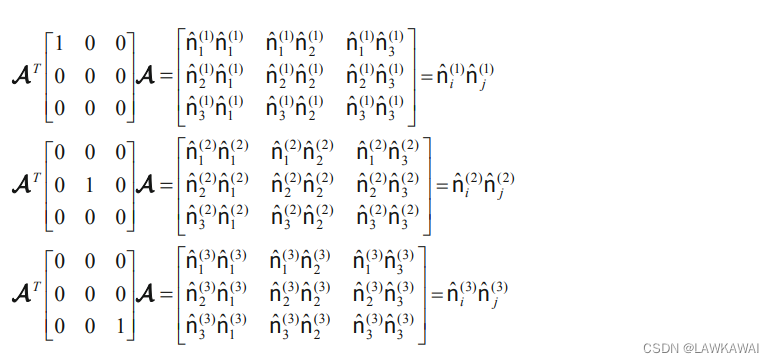
因此，可以将二阶张量的分量用特征值和特征向量的函数表示（谱表示）：
$$T_{ij}=T_1{\hat{n}}_i^{(1)}{\hat{n}}_j^{(1)}+T_2{\hat{n}}_i^{(2)}{\hat{n}}_j^{(2)}+T_3{\hat{n}}_i^{(3)}{\hat{n}}_j^{(3)}$$
张量表示：
$$T=T_1{\hat{n}}^{(1)}⨂{\hat{n}}^{(1)}+T_2{\hat{n}}^{(2)}⨂{\hat{n}}^{(2)}+T_3{\hat{n}}^{(3)}⨂{\hat{n}}^{(3)}$$

张量可以表示成并矢的线性组合：
$$\boxed{T=\sum _{a=1}^3{T}_a{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}}(二阶张量的谱表示)$$
NOTE： 也可以从定义得到：
因为$1={\hat{n}}_i⨂{\hat{n}}_i$， 所以表示成$1={\sum }_{a=1}^3{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}$，那么：
$$\begin{gathered} T=T\cdot 1=T\cdot (\sum _{a=1}^3{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}) \\ =\sum _{a=1}^{3}T\cdot {\hat{n}}^{(a)}⨂{\hat{n}}^{(a)} \\ =\sum _{a=1}^3{T}_a{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)} \end{gathered}$$

其中，用到了特征值和特征向量的定义：$T\cdot {\hat{n}}^{(a)}=T_a{\hat{n}}^{(a)}$

现在，考虑一个正交张量$R$，将正交变换作用到一个单位向量$\hat{N}$，得到一个单位向量$\hat{n}$， $\hat{n}=R\cdot \hat{N}$，因此，可以将正交张量$R$ 表示成：
$$\begin{gathered} R=R\cdot 1=R\cdot (\sum _{a=1}^3{\hat{N}}^{(a)}⨂{\hat{N}}^{(a)}) \\ =\sum _{a=1}^{3}R\cdot {\hat{N}}^{(a)}⨂{\hat{N}}^{(a)} \\ =\sum _{a=1}^3{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)} \end{gathered}$$

张量的谱表示在张量代数操作种是非常有用的，比如在主空间的张量的幂可以表示成：

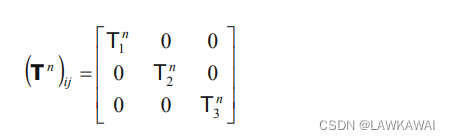
所以$T^n$ 的谱表示为：
$$T^n=\sum _{a=1}^3{T}_a^n{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}$$

同样，$\sqrt{T}$的谱表示为：
$$\sqrt{T}=\sum _{a=1}^3\sqrt{T_a}{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}$$

然后，我们考虑一个正定张量，有正的特征值，条件是: $\hat{x}\cdot T\cdot \hat{x}\ge 0$，将此条件转化成谱表示：

$$\begin{gathered} \hat{x}\cdot T\cdot \hat{x}\ge 0 \\ ⟹\hat{x}\cdot (\sum _{a=1}^3{T}_a{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)})\cdot \hat{x}\ge 0 \\ ⟹\sum _{a=1}^3{T}_a\hat{x}\cdot {\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}\cdot \hat{x}\ge 0 \\ ⟹\sum _{a=1}^3{T}_a[\hat{x}\cdot {\hat{n}}^{(a)}{]}^2\ge 0 \\ ⟹T_1(\hat{x}\cdot {\hat{n}}^{(1)}{)}^2+T_2(\hat{x}\cdot {\hat{n}}^{(2)}{)}^2+T_3(\hat{x}\cdot {\hat{n}}^{(3)}{)}^2\ge 0 \end{gathered}$$

以上表达式在$\hat{x}\ne 0$才成立

当$\hat{x}=\hat{n}$，上式变成 $T_1({\hat{n}}^{(1)}\cdot {\hat{n}}^{(1)}{)}^2=T_1\ge 0$， 表示当张量是半正定，特征值大于等于0。因此张量是正定的，当且仅当特征值都为正的，不等于0

小结：正定张量的迹大于0，如果正定张量的迹为0，表示张量是个零张量

四阶张量的谱表示：
四阶张量$II$的定义：

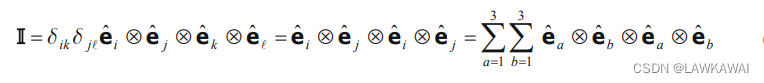
由于$II$ 是各向同性张量，所以也可以把它表示成任何正交基${\hat{n}}^{(a)}$：
$$II=\sum _{a=1}^3\sum _{b=1}^3{\hat{n}}^{(a)}⨂{\hat{n}}^{(b)}⨂{\hat{n}}^{(a)}⨂{\hat{n}}^{(b)}$$

同理，可以得到$\overline{II}和\underline{II}$的谱表示：

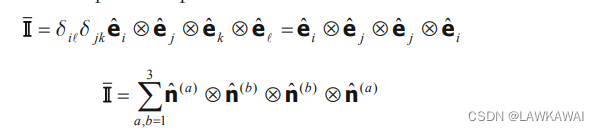
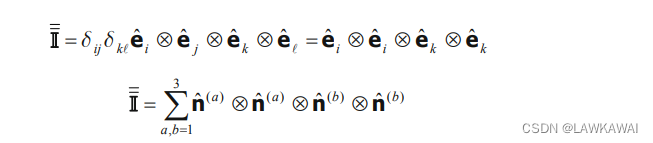
问题1.34 $W$是反对称二阶张量，$V$ 是正定对称张量，其谱表示为：$V={\sum }_{a=1}^3{\lambda }_a{\hat{n}}^{(a)}⨂{\hat{n}}^{(a)}$，证明：$W$ 可以表示成：$W={\sum }_{a,b=1,a\ne b}^3{W}_{ab}{\hat{n}}^{(a)}⨂{\hat{n}}^{(b)}$； 且证明：$W\cdot V-V\cdot W={\sum }_{a,b=1,a\ne b}^3{W}_{ab}({\lambda }_b-{\lambda }_a){\hat{n}}^{(a)}⨂{\hat{n}}^{(b)}$

Cayley-Hamilton 定理

Cayley-Hamilton 定理： 对于任意张量$T$，满足特征方程，特征值满足${\lambda }^3-{\lambda }^2{I}_T+\lambda I{I}_T-II{I}_T=0$，所以张量$T$：
$$T^3-T^2{I}_T+TI{I}_T-II{I}_T=0$$

Cayley-Hamilton 定理的应用：表示张量的幂
$$\begin{gathered} T^3\cdot T-T^2\cdot T{I}_T+T\cdot TI{I}_T-II{I}_{T}1\cdot T=0 \\ ⟹T^4=T^3{I}_T-T^{2}I{I}_T+TII{I}_T \end{gathered}$$

应用Cayley-Hamilton 定理， 可以将第三不变量表示成迹的函数：
$$T^3:1-T^2:1I_T+T:1I{I}_T-II{I}_{T}1:1=0:1$$
由于：
$$\begin{gathered} T^3:1=Tr(T^3); \\ {T}^2:1=Tr(T^2); \\ T:1=Tr(T); \\ 1:1=Tr(1)=3; \\ 0:1=Tr(0)=0 \end{gathered}$$
所以：
$$\begin{gathered} Tr(T^3)-I_{T}Tr(T^2)+I{I}_{T}Tr(T)-3II{I}_T=0 \\ ⟹II{I}_T=\frac{1}{3}(Tr(T^3)-I_{T}Tr(T^2)+I{I}_{T}Tr(T)) \end{gathered}$$

将不变量代入：

得到：
$II{I}_T=\frac{1}{3}(Tr(T^3)-\frac{3}{2}Tr(T^2)Tr(T)+\frac{1}{2}[Tr(T){]}^3)$
指标形式：
$II{I}_T=\frac{1}{3}(T_{ij}{T}_{jk}{T}_{ki}-\frac{3}{2}{T}_{ij}{T}_{ji}{T}_{kk}+\frac{1}{2}{T}_{ii}{T}_{jj}{T}_{kk})$

问题1.35 基于Cayley-Hamilton 定理，用张量幂求出张量的逆

n×n矩阵$A_{n\times n}$，那么特征行列式为：
$$|\lambda 1_{n\times n}-A|=0$$
展开，得：
$${\lambda }^n-I_1{\lambda }^{n-1}+I_2{\lambda }^{n-2}-...(-1{)}^n{I}_n=0$$
其中$I_1,I_2,...,I_n$是A的不变量，n=3是二阶张量的情况

应用Cayley-Hamilton 定理，
$$A^n-I_1{A}^{n-1}+I_2{A}^{n-2}-...+(-1{)}^n{I}_{n}1=0$$
通过乘以$A^{-1}$，可以得到：
$$\begin{gathered} A^n{A}^{-1}-I_1{A}^{n-1}{A}^{-1}+I_2{A}^{n-2}{A}^{-1}-...+(-1{)}^n{I}_{n}1A^{-1}=0 \\ ⟹A^{n-1}-I_1{A}^{n-2}+I_2{A}^{n-3}-...+(-1{)}^{n-1}{I}_{n-1}1+(-1{)}^n{I}_n{A}^{-1}=0 \end{gathered}$$

那么：
$$A^{-1}=\frac{(-1{)}^{n-1}}{I_n}(A^{n-1}-I_1{A}^{n-2}+I_2{A}^{n-3}-...+(-1{)}^{n-1}{I}_{n-1}1)$$
只有当$I_n=\det A\ne 0$，$A^{-1}$才存在

问题1.36 验证Cayley-Hamilton 定理

参考教材：
Eduardo W.V. Chaves， Notes On Continuum Mechanics