算法示例:LeetCode300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
法一:利用算法套路十五——最长公共子序列LCS求最长公共子序列
对原数组 nums 去重并排序,存储在数组 sorted_nums 中,并求sorted_nums与nums的最长公共子序列,这即是最长递增子序列
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n=len(nums)
if n==1:
return 1
# 将原问题转化为求最长公共子序列
sorted_nums = sorted(list(set(nums)))
return self.longestCommonSubsequence(nums,sorted_nums)
# 求最长公共子序列
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
n, m = len(text1), len(text2)
dp = [[0]*(m+1) for _ in range(n + 1)]
for i in range(n):
for j in range(m):
if text1[i]==text2[j]:
dp[i+1][j+1]=dp[i][j]+1
else:
dp[i+1][j+1]=max(dp[i][j + 1], dp[i + 1][j])
return dp[n][m]
法二:递归+记忆化搜索
法一:选或不选的思路
定义一个函数 dfs,从大问题往子问题递归,它返回从数组开头到第 i 个位置(包括第 i 个位置)的最长上升子序列的长度,num记录当前递增子序列的最小值,之后加入的数需要小于num。
- 在每个位置 i 上,都要枚举两种情况:若满足条件可以将 nums[i] 加入递增子序列;不加入子序列。
- 如果nums[i]<num,可以选择将 nums[i] 加入,更新num为当前的nums[i],递归dfs(i-1,nums[i]),
- 选择不加入,那么忽略当前元素,不需要更新num,向前递归dfs(i-1,num)。
- 取两者中较大的值作为结果。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
@cache
def dfs(i:int,num: int)->int:
if i<0:
return 0
#选
len1=0
if nums[i]<num:
len1=dfs(i-1,nums[i])+1
#不选
len2=dfs(i-1,num)
return max(len1,len2)
return dfs(len(nums)-1,100000)
法二:选哪个的思路
- 定义函数 dfs,它将递归计算以第 i个位置结尾的 LIS 的长度,并将结果缓存。对于数组中每个位置,我们检查在这个位置之前的所有元素中是否有小于当前位置的元素,如果存在,则可以选择这个元素并继续递归计算以其结尾的 LIS;否则,当前位置自成长度为1的 LIS。
- 在计算过程中使用了缓存级联性。具体来说,假设现在需要求出从某个位置 i 开始的值,则需要用到从位置 0到位置 i - 1所有位置计算出的结果。由于从位置 0开始开始的值可能会被多次调用,缓存机制确保了不必重复计算已经计算过的子问题。
- 在主函数中,对于数组中的每个元素,都递归调用一次dfs(i)`函数计算从该位置结尾的 LIS 长度。最后,返回所有 LIS 长度中的最大值即可。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
@cache
def dfs(i: int) -> int:
res = 0 # 初始答案 0
for j in range(i):
# 枚举选哪个,如果 nums[j] < nums[i],则将 nums[j] 加入该递增序列,并继续递归dfs(j)
if nums[j] < nums[i]:
res = max(res, dfs(j))
return res + 1 # 最后返回以 nums[i] 结尾的 LIS 的长度
# 对于数组中的每个位置,都递归调用一次 dfs 函数计算以该位置结尾的 LIS 长度,然后返回最大值
return max(dfs(i) for i in range(len(nums)))
法三:动态规划
- 初始化 dp 数组,
dp[i] 为仅考虑前 i 个元素,且以nums[i] 结尾的最长上升子序列的长度,且子序列需要与原始数组中数的顺序不变,即使第i个元素之后的元素小于nums[i] ,也不能加入到上升子序列。因此整个数组中以nums[i]结尾的最长上升子序列的长度就是仅考虑前 i 个元素的最长上升子序列的长度,故dp[i]就是整个数组中以nums[i]结尾的最长上升子序列的长度。 - 采用选哪个的思路,遍历每个元素 nums[i],在其前面的所有元素 nums[ j ]中查找比它小的元素,更新 dp[i] 的值。如果 nums[i] > nums[j],则说明 nums[i] 可以接在 nums[j] 后面构成一个更长的上升子序列,此时需要更新 dp[i] 的值为 dp[j] + 1,表示以 nums[i] 结尾的最长上升子序列的长度为 dp[j] + 1。其中 dp[j] 表示以 nums[j] 结尾的最长上升子序列的长度。
- 最后返回 dp 数组中的最大值即可,即整个数组的最长上升子序列的长度。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# 初始化 dp 数组,dp[i] 表示以 nums[i] 结尾的最长上升子序列的长度
dp = [1] * len(nums) # 初始值都为 1
# 遍历每个元素,在其前面的所有元素中查找小于它的元素
for i in range(len(nums)):
#j的范围从0到i-1,故在更新dp[i]=dp[j]+1时dp[j]已经代表以nums[j]结尾的最长上升子序列的长度
for j in range(i):
if nums[j]<nums[i] :
#判断是否更新dp[i]
dp[i] = max(dp[i], dp[j] + 1)
# 返回 dp 数组中的最大值即可,即整个数组的最长上升子序列的长度
return max(dp)
时间优化:贪心+二分查找
具体来说,我们维护一个变量ng记录当前最长的上升子序列的长度,然后遍历整个nums 数组,对于每个元素x,使用二分查找找到第一个大于等于x的位置j,如果j等于当前最长上升子序列长度ng,说明x大于nums[:ng]中的所有元素,因此将x插入到nums的末尾并将ng加1,保证nums[:ng]中的所有元素都是当前最长的上升子序列。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
ng = 0 # 记录当前最长的上升子序列的长度
for x in nums: # 遍历 nums 数组
j = bisect_left(nums, x, 0, ng) # 找到第一个大于等于 x 的位置 j
nums[j] = x # 将 nums[j] 修改为 x
if j == ng: # 如果 j 等于当前的最长上升子序列的长度,则更新 ng
ng += 1
return ng # 返回最长上升子序列的长度
算法练习一:LeetCode1964. 找出到每个位置为止最长的有效障碍赛跑路线
你打算构建一些障碍赛跑路线。给你一个 下标从 0 开始 的整数数组 obstacles ,数组长度为 n ,其中 obstacles[i] 表示第 i 个障碍的高度。
对于每个介于 0 和 n - 1 之间(包含 0 和 n - 1)的下标 i ,在满足下述条件的前提下,请你找出 obstacles 能构成的最长障碍路线的长度:
你可以选择下标介于 0 到 i 之间(包含 0 和 i)的任意个障碍。
在这条路线中,必须包含第 i 个障碍。
你必须按障碍在 obstacles 中的 出现顺序 布置这些障碍。
除第一个障碍外,路线中每个障碍的高度都必须和前一个障碍 相同 或者 更高 。
返回长度为 n 的答案数组 ans ,其中 ans[i] 是上面所述的下标 i 对应的最长障碍赛跑路线的长度。
该题就是求以每个数结尾的最长上升子序列,对示例返回值稍作修改直接调用
func longestObstacleCourseAtEachPosition(obstacles []int) []int {
return lengthOfIS(obstacles)
}
func lengthOfIS(nums []int)[]int{
n:=len(nums)
dp:=make([]int,n)
for i:=0;i<n;i++{
dp[i]=1
}
for i:=0;i<n;i++{
for j:=0;j<i;j++{
if nums[j]<=nums[i]{
dp[i]=max(dp[i],dp[j]+1)
}
}
}
return dp
}
func max(a,b int)int{if a>b{return a};return b}
算法练习二:LeetCode354. 俄罗斯套娃信封问题
给你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
注意:不允许旋转信封。
本题可以看做就是二维层面的最长递增问题,只需要在判断是否满足递增时注意判断宽度与高度是否都满足条件即可。
其次,需要注意本题不需要满足套娃的信封是子序列,即信封的顺序可以改变,因此我们可以在求最长递增之前将二维数组按某一维进行升序排列,这样就可以直接套用最长递增子序列的求解思路。
func maxEnvelopes(envelopes [][]int) int {
n := len(envelopes)
dp := make([]int, n)
for i := 0; i < n; i++ {
dp[i] = 1 // 初始值为 1(每个信封自身也算一个 LIS)
}
// 按照宽度升序排序,若宽度相同则按照高度升序排序
sort.Slice(envelopes, func(i, j int) bool {
if envelopes[i][0] == envelopes[j][0] {
return envelopes[i][1] < envelopes[j][1]
}
return envelopes[i][0] < envelopes[j][0]
})
// 计算 LIS 长度
for i := 1; i < n; i++ {
for j := 0; j < i; j++ {
if envelopes[j][0] < envelopes[i][0] && envelopes[j][1] < envelopes[i][1] {
dp[i] = max(dp[i], dp[j]+1)
}
}
}
// 取 dp 数组的最大值作为答案
return max(dp...)
}
func max(nums ...int) int {
// 不定参数函数,返回所有参数中的最大值
res := nums[0]
for _, num := range nums[1:] {
if num > res {
res = num
}
}
return res
}
算法练习三:LeetCode1626. 无矛盾的最佳球队
假设你是球队的经理。对于即将到来的锦标赛,你想组合一支总体得分最高的球队。球队的得分是球队中所有球员的分数 总和 。
然而,球队中的矛盾会限制球员的发挥,所以必须选出一支 没有矛盾 的球队。如果一名年龄较小球员的分数 严格大于 一名年龄较大的球员,则存在矛盾。同龄球员之间不会发生矛盾。
给你两个列表 scores 和 ages,其中每组 scores[i] 和 ages[i] 表示第 i 名球员的分数和年龄。请你返回 所有可能的无矛盾球队中得分最高那支的分数 。
此题与上题类似,也是二维的最长递增子序列问题,按照分数从小到大排序,分数相同的按照年龄从小到大排序,之后计算所有位置的最长递增子序列。
不过此题的状态转移方程有所不同,为
d
p
[
i
]
=
m
a
x
(
d
p
[
j
]
)
+
s
c
o
r
e
s
[
i
]
dp[i]=max(dp[j])+scores[i]
dp[i]=max(dp[j])+scores[i]
\func bestTeamScore(scores []int, ages []int) int {
n := len(scores)
dp := make([]int, n) // dp[i] 表示前 i 个球员中,最后一个球员年龄为 i 时的得分最大值
ballplayer := make([][]int, n) // 将每个球员的分数和年龄组成二元组,用于排序
for i := 0; i < n; i++ {
ballplayer[i] = []int{scores[i], ages[i]} // 初始化二元组
}
// 按照分数升序排序,若分数相同则按照年龄升序排序
sort.Slice(ballplayer, func(i, j int) bool {
if ballplayer[i][0] == ballplayer[j][0] {
return ballplayer[i][1] < ballplayer[j][1]
}
return ballplayer[i][0] < ballplayer[j][0]
})
// 计算所有以当前位置为结尾的最大得分
for i := 0; i < n; i++ {
for j := 0; j < i; j++ {
// 如果第 j 名球员的年龄不超过第 i 名球员,则可以将第 i 名球员加入到以第 j 名球员结尾的最优子序列中
if ballplayer[j][1] <= ballplayer[i][1] {
dp[i] = max(dp[i], dp[j])
}
}
dp[i] += ballplayer[i][0] // 加上第 i 名球员的得分
}
// 返回所有最大得分中的最大值
return max(dp...)
}
func max(nums ...int) int {
// 不定参数函数,返回所有参数中的最大值
res := nums[0]
for _, num := range nums[1:] {
if num > res {
res = num
}
}
return res
}
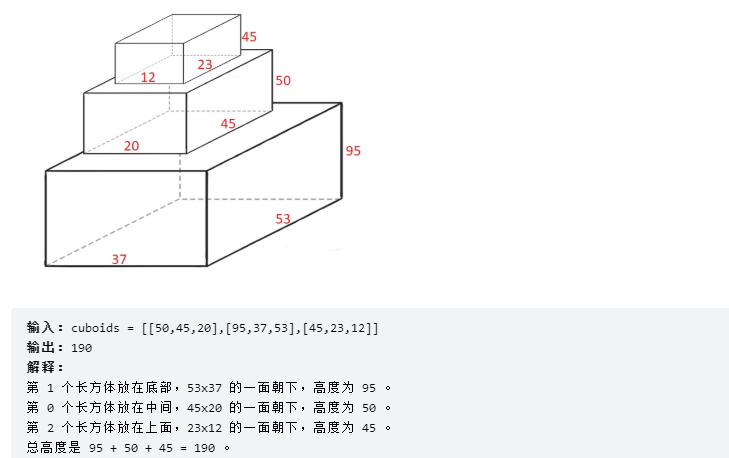
算法练习四:LeetCode1691. 堆叠长方体的最大高度
给你 n 个长方体 cuboids ,其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti](下标从 0 开始)。请你从 cuboids 选出一个 子集 ,并将它们堆叠起来。
如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ,你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列,以将它放在另一个长方体上。
返回 堆叠长方体 cuboids 可以得到的 最大高度 。
此题与上题类似,不过是三维的最长递增子序列问题,且本题的三个维度可以相互转变。
因此我们首先将每个立方体的长、宽、高都按从小到大的顺序排列,并且按照边长从小到大排列所有立方体,之后按照求解最长递增子序列的思路来求该题的最高高度。
func maxHeight(cuboids [][]int) (ans int) {
// 将每个立方体的长、宽、高从小到大排序
for _, c := range cuboids {
sort.Ints(c)
}
// 将立方体按照边长排序
sort.Slice(cuboids, func(i, j int) bool {
a, b := cuboids[i], cuboids[j]
return a[0] < b[0] || a[0] == b[0] && (a[1] < b[1] || a[1] == b[1] && a[2] < b[2])
})
//经过以上处理保证了每个立方体的长、宽、高都按从小到大的顺序排列,并且按照边长从小到大排列所有立方体
// dp[i] 表示选取第 i 个立方体作为堆栈底部时,可以构成的最大高度
dp := make([]int, len(cuboids))
for i, c2 := range cuboids {
for j, c1 := range cuboids[:i] {
if c1[1] <= c2[1] && c1[2] <= c2[2] { // 满足垒叠条件,则更新状态
dp[i] = max(dp[i], dp[j]) // c1 可以堆在 c2 上
}
}
dp[i] += c2[2] // c2 的高度加上上面堆起来的立方体的高度,就是总高度
ans = max(ans, dp[i]) // 更新最大高度
}
return
}
func max(a,b int)int{if a>b{return a};return b}
算法进阶一:LeetCode673. 最长递增子序列的个数
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
注意 这个数列必须是 严格 递增的。
- 定义 dp[i] 表示以第 i 个元素为结尾的最长上升子序列的长度,求解过程与上题一样。
- 同时定义 cnt[i] 表示以第 i 个元素为结尾的最长上升子序列的数量(可能包含多个)。
- 遍历 nums 数组,对于每个位置 i 和其前面的位置 j,如果当前元素 nums[i] 大于 nums[j],则可以将 nums[i] 加入以 nums[j] 结尾的 LIS 中。此时比较 dp[i] 和 dp[j]+1 的大小:如果 dp[j]+1 大于 dp[i],说明以 j 结尾的 LIS 加上 num[i] 更优,则更新 dp[i] 和 cnt[i];如果 dp[j]+1 等于 dp[i],则说明多了一个以 i 结尾的 LIS,则仅更新 cnt[i](不更新 dp[i]),且注意更新 cnt[i]时都是加上cnt[j],而不是1。
- 遍历 dp 数组,计算最大的 dp[i] 值作为整个数组的 LIS 长度,并统计拥有该长度的最长上升子序列的数量之和。
func findNumberOfLIS(nums []int) int {
n := len(nums)
// 初始化动态规划数组和计数数组,长度均为 n
dp := make([]int, n) // dp[i] 表示以 nums[i] 结尾的最长递增子序列长度
cnt := make([]int, n) // cnt[i] 表示以 nums[i] 结尾且长度为 dp[i] 的递增子序列数量
for i := 0; i < n; i++ {
dp[i] = 1 // 初始值为 1(每个数自身也算一个 LIS)
cnt[i] = 1 // 初始值为 1,表示单独一个数也构成一个长度为 1 的 LIS
}
// 计算所有以当前位置为结尾的递增子序列
for i := 0; i < n; i++ {
for j := 0; j < i; j++ {
if nums[j] < nums[i] {
// 如果可以将 nums[i] 接在 nums[j] 后面形成一个更长的递增子序列,
// 则更新 dp[i] 并将 cnt[i] 设为 cnt[j],即以 nums[j] 结尾的递增子序列可以延续到 nums[i]
if dp[j]+1 > dp[i] {
dp[i] = dp[j] + 1
cnt[i] = cnt[j]
} else if dp[j]+1 == dp[i] {
// 如果接上 nums[i] 后仍然是 dp[i] 长度的递增子序列,则将以 nums[j] 结尾的递增子序列数量累加到 cnt[i]
cnt[i] += cnt[j]
}
}
}
}
// 找到最长递增子序列的长度和数量
maxLen := 0 // 最长递增子序列的长度
res := 0 // 最长递增子序列的数量
for i := 0; i < n; i++ {
if dp[i] > maxLen {
maxLen = dp[i]
res = cnt[i]
} else if dp[i] == maxLen {
res += cnt[i]
}
}
return res
}
func max(a, b int) int {if a > b { return a}; return b}
算法进阶二:LeetCode1671. 得到山形数组的最少删除次数
我们定义 arr 是 山形数组 当且仅当它满足:
arr.length >= 3
存在某个下标 i (从 0 开始) 满足 0 < i < arr.length - 1 且:
arr[0] < arr[1] < … < arr[i - 1] < arr[i]
arr[i] > arr[i + 1] > … > arr[arr.length - 1]
给你整数数组 nums ,请你返回将 nums 变成 山形状数组 的 最少 删除次数。
使用最长递增子序列(LIS)的方法来解决得到山形数组的最少删除次数问题,可以先将该问题转化为求最长的单峰子序列长度。
具体地,我们可以对于原山形数组,将其分为左右两个方向,每个部分都计算出最长递增子序列(LIS),分别用left[i]表示原数组的前i个元素的最长递增子序列长度,right[i]表示原数组的后n-i个元素的最长递减子序列长度(即将原数组反转后求得)。然后,对于一个山形数组,可以确定一个峰值,使得左半部分的LIS和右半部分的LIS能够在这个峰值处拼接成为单峰子序列。
那么,我们可以枚举峰值的位置(注意峰值需要满足不在第一个或最后一个位置,且左、右的最长递增子序列长度都大于1),分别计算其左右部分的LIS,并将它们相加作为单峰子序列的长度。最终,我们可以取所有可能峰值位置所得长度中的最大值即为所求的最短删除次数。
func minimumMountainRemovals (nums []int) int {
n := len(nums)
left, right := make([]int, n), make([]int, n)
// 计算左半部分最长递增子序列
for i := range nums {
left[i] = 1
for j := 0; j < i; j++ {
if nums[j] < nums[i] {
left[i] = max(left[i], left[j]+1)
}
}
}
// 计算右半部分最长递增子序列
for i := n - 1; i >= 0; i-- {
right[i] = 1
for j := n - 1; j > i; j-- {
if nums[j] < nums[i] {
right[i] = max(right[i], right[j]+1)
}
}
}
ans := 0
// 枚举峰值位置,且峰值不能在第一个或者最后一个位置,计算单峰子序列长度
for i := 1; i < n-1; i++ {
//只有当左、右的最长递增子序列长度都大于1时,当前节点才能作为峰值
if left[i] > 1 && right[i] > 1 {
ans = max(ans, left[i]+right[i]-1)
}
}
return n - ans
}
func max(a, b int) int {if a > b {return a};return b
}