区间预测 | MATLAB实现QRCNN-BiGRU卷积双向门控循环单元分位数回归时间序列区间预测

news2024/10/5 13:40:57

区间预测 | MATLAB实现QRCNN-BiGRU卷积双向门控循环单元分位数回归时间序列区间预测

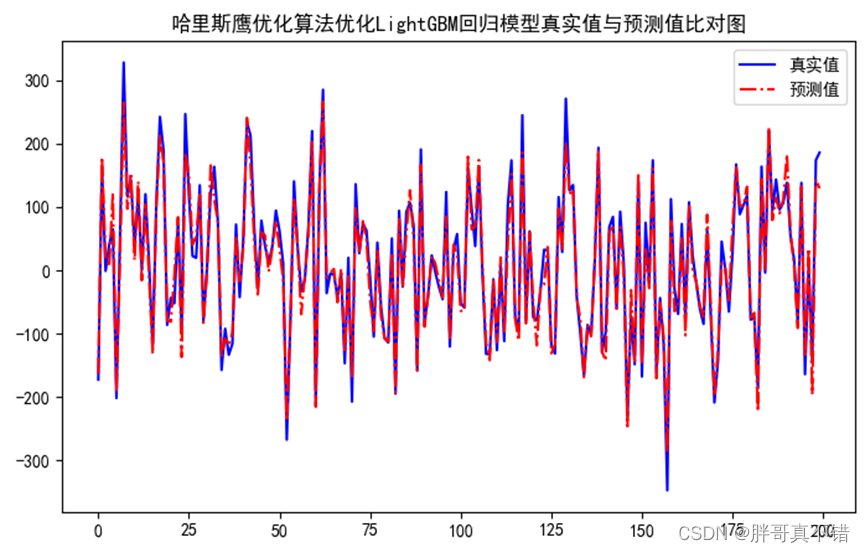
效果一览

基本介绍

1.Matlab实现基于QRCNN-BiGRU分位数回归卷积双向门控循环单元的时间序列区间预测模型；
2.多图输出、多指标输出(MAE、RMSE、MSE、R2)，多输入单输出，含不同置信区间图、概率密度图；
3.data为数据集，功率数据集，用过去一段时间的变量，预测目标，目标为最后一列，也可适用于负荷预测、风速预测；MainQRCNN_BiGRUTS为主程序，其余为函数文件，无需运行；
4.代码质量高，注释清楚，含数据预处理部分，处理缺失值，如果为nan，用上一行替代，也含核密度估计。

模型描述

QRCNN-BiGRU模型结合了卷积神经网络和双向门控循环单元，用于时间序列数据的分位数回归和区间预测。
分位数回归是一种回归分析方法，用于预测数据在不同分位数下的值，比如中位数、上四分位数、下四分位数等。区间预测则是指预测数据在一个给定的时间范围内的取值范围。
因此，QRCNN-BiGRU模型可以用于时间序列数据的分位数回归和区间预测，具有较好的预测性能。
QRCNN-BiGRU模型的具体公式可以分为两部分，一部分是QRCNN的公式，另一部分是BiGRU的公式。

QRCNN部分的公式如下：
输入数据为 $\in R^{n \times p}$ ，其中 $n$ 是时间序列的长度， $p$ 是每个时间步的特征数。
卷积层：
$z^c_{i,j} = f(\sum_{k=1}^p W^c_{j,k} \ast x_{i,k} + b^c_j)$
其中 $z^c_{i,j}$ 是第 $i$ 个时间步的第 $j$ 个卷积核的输出， $W^c_{j,k}$ 是第 $j$ 个卷积核的第 $k$ 个权重， $\ast$ 表示卷积操作， $b^c_j$ 是第 $j$ 个卷积核的偏置， $f$ 是激活函数。
最大池化层：
$z^p_{i,j} = \max_{k=1}^{l}(z^c_{i,j+k-1})$
其中 $z^p_{i,j}$ 是第 $i$ 个时间步的第 $j$ 个卷积核的最大池化输出， $l$ 是池化窗口大小。
全连接层：
$z^f_i = g(\sum_{j=1}^q W^f_{i,j} z^p_{i,j} + b^f_i)$
其中 $z^f_i$ 是第 $i$ 个时间步的全连接层输出， $W^f_{i,j}$ 是第 $i$ 个神经元连接到第 $j$ 个池化输出的权重， $b^f_i$ 是第 $i$ 个神经元的偏置， $g$ 是激活函数。
输出层：
$\hat{y}_i = \sum_{j=1}^k q_j z^f_i + b$
其中 $\hat{y}_i$ 是第 $i$ 个时间步的预测值， $q_j$ 是第 $j$ 个分位数的权重， $b$ 是偏置。
BiGRU部分的公式如下：
输入数据为 $\in R^{n \times p}$ ，其中 $n$ 是时间序列的长度， $p$ 是每个时间步的特征数。
前向GRU：
$z^f_t = \sigma(W^f x_t + U^f h_{t-1} + b^f) \\ r^f_t = \sigma(W_r^f x_t + U_r^f h_{t-1} + b_r^f) \\ \tilde{h}_t^f = \tanh(W_h^f x_t + r_t^f \odot U_h^f h_{t-1} + b_h^f) \\ h_t^f = (1 - z_t^f) \odot h_{t-1}^f + z_t^f \odot \tilde{h}_t^f$
其中 $z^f_t$ 是前向GRU的更新门， $r^f_t$ 是重置门， $\tilde{h}_t^f$ 是候选隐藏状态， $h_t^f$ 是前向GRU的隐藏状态。
后向GRU：
$z^b_t = \sigma(W^b x_t + U^b h_{t+1} + b^b) \\ r^b_t = \sigma(W_r^b x_t + U_r^b h_{t+1} + b_r^b) \\ \tilde{h}_t^b = \tanh(W_h^b x_t + r_t^b \odot U_h^b h_{t+1} + b_h^b) \\ h_t^b = (1 - z_t^b) \odot h_{t+1}^b + z_t^b \odot \tilde{h}_t^b$
其中 $z^b_t$ 是后向GRU的更新门， $r^b_t$ 是重置门， $\tilde{h}_t^b$ 是候选隐藏状态， $h_t^b$ 是后向GRU的隐藏状态。
将前向和后向GRU的隐藏状态拼接起来：
$h_t = [h_t^f ; h_t^b]$
最终输出层的公式为：
$\hat{y}_i = \sum_{j=1}^k q_j h_i + b$
其中 $\hat{y}_i$ 是第 $i$ 个时间步的预测值， $q_j$ 是第 $j$ 个分位数的权重， $b$ 是偏置。

程序设计

完整程序和数据获取方式：私信博主。

% 加载数据
load example_data.mat

% 分割数据集
train_ratio = 0.7;
validation_ratio = 0.2;
test_ratio = 0.1;
[train_data, validation_data, test_data] = split_data(data, train_ratio, validation_ratio, test_ratio);

% 设置超参数
num_epochs = 100;
batch_size = 32;
learning_rate = 0.001;
num_conv_filters = 32;
conv_filter_size = 3;
pooling_size = 2;
num_hidden_units = 64;
num_quantiles = 3;

% 训练模型
model = train_qrcnn_bigru(train_data, validation_data, num_epochs, batch_size, learning_rate, num_conv_filters, conv_filter_size, pooling_size, num_hidden_units, num_quantiles);

% 测试模型
[test_loss, test_predictions] = test_qrcnn_bigru(model, test_data);

% 可视化结果
plot_results(test_data, test_predictions);
function [train_data, validation_data, test_data] = split_data(data, train_ratio, validation_ratio, test_ratio)
% 分割数据集
total_length = size(data, 1);
train_length = floor(total_length * train_ratio);
validation_length = floor(total_length * validation_ratio);
test_length = total_length - train_length - validation_length;

train_data = data(1:train_length, :);
validation_data = data(train_length+1:train_length+validation_length, :);
test_data = data(train_length+validation_length+1:end, :);
end

function model = train_qrcnn_bigru(train_data, validation_data, num_epochs, batch_size, learning_rate, num_conv_filters, conv_filter_size, pooling_size, num_hidden_units, num_quantiles)
% 训练QRCNN-BiGRU模型
input_size = size(train_data, 2) - 1;

% 构建模型
input_layer = sequenceInputLayer(input_size);
conv_layer = convolution1dLayer(conv_filter_size, num_conv_filters, 'Padding', 'same');
pool_layer = maxPooling1dLayer(pooling_size, 'Stride', 2);
flatten_layer = flattenLayer();
fc_layer = fullyConnectedLayer(num_hidden_units);
gru_layer = bidirectionalgruLayer(num_hidden_units, 'OutputMode', 'last');
output_layer = qrcnnRegressionLayer(num_quantiles);

% 组装网络层
layers = [input_layer;
          conv_layer;
          pool_layer;
          flatten_layer;
          fc_layer;
          gru_layer;
          output_layer];

% 设置训练选项
options = trainingOptions('adam', ...
                          'MaxEpochs', num_epochs, ...
                          'MiniBatchSize', batch_size, ...
                          'InitialLearnRate', learning_rate, ...
                          'ValidationData', validation_data, ...
                          'ValidationFrequency', 10, ...
                          'ValidationPatience', 5, ...
                          'CheckpointPath', tempdir);

% 训练模型
model = trainNetwork(train_data, layers, options);
end

function [test_loss, test_predictions] = test_qrcnn_bigru(model, test_data)
% 测试QRCNN-BiGRU模型
test_sequences = test_data(:, 2:end)';
num_test_samples = size(test_sequences, 2);
test_labels = test_data(:, 1);

% 测试模型
test_predictions = predict(model, test_sequences, 'MiniBatchSize', 1);

% 计算测试集损失
test_loss = qrcnnLoss(test_labels', test_predictions);

% 将预测结果转换为列向量
test_predictions = test_predictions(:);
end

function plot_results(test_data, test_predictions)
% 可视化测试结果
test_labels = test_data(:, 1);
num_test_samples = length(test_labels);

% 绘制真实值和预测值的对比图
figure;
plot(1:num_test_samples, test_labels, 'b-', 1:num_test_samples, test_predictions, 'r-');
xlabel('Time Step');
ylabel('Value');
legend('True', 'Predicted');

% 绘制预测误差的直方图
prediction_errors = test_predictions - test_labels;
figure;
histogram(prediction_errors);
xlabel('Prediction Error');
ylabel('Frequency');
end