hunan Problem E. 矩阵游戏

Attachments - 2023 CCPC Henan Provincial Collegiate Programming Contest - Codeforces

 

 

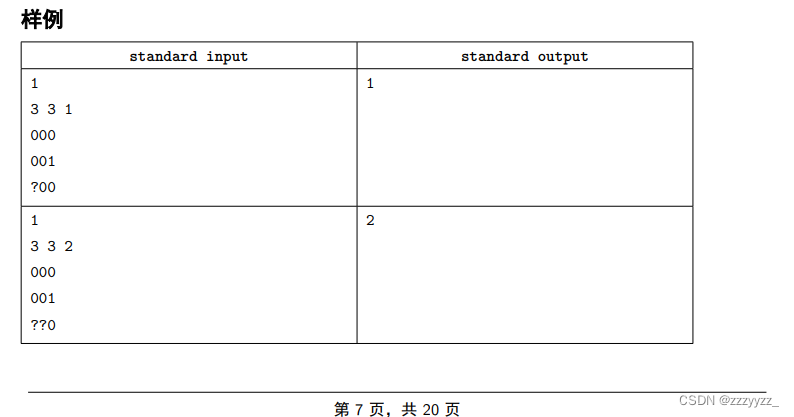
思路：

我们考虑用dp,定义f[i][j][k],代表从1,1走到i,j并且使用k次变换操作能够获得的最大

价值，那么类似于01背包，接下来是转移方程

if(str[i][j]=='0') f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k]);

else if(str[i][j]=='1') f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k])+1;

else {

        if(k-1>=0) f[i][j][k]=max(f[i-1][j][k-1],f[i][j-1][k-1])+1;

        else f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k]);

}

但是直接用三维数组会mle，然后我们观察到，ｄｐ数组使用i-１与ｉ所以我们可以使用滚动数组优化掉一维，那么接下来就是ｄｐ了　        

#include<iostream>
#include<cstring>
#include<string>
#include<sstream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<vector> 
#include<set>
#include<unordered_map>
#include<ctime>
#include<cstdlib>
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
typedef pair<int,pair<int,int> > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
char str[510][510];
int f[2][510][1010];

void solve() {
	n=read(),m=read();
	int x=read();
	
	for(int i=1;i<=n;i++) scanf("%s",str[i]+1);
	
	for(int i=0;i<2;i++) {
		for(int j=1;j<=m;j++) {
			for(int k=0;k<=x;k++) {
				f[i][j][k]=0;
			}
		}
	}
	 
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			for(int k=0;k<=x;k++) {
				int a=i&1,b=(i-1)&1;
				if(str[i][j]=='0') f[a][j][k]=max(f[b][j][k],f[a][j-1][k]);
				else if(str[i][j]=='1') f[a][j][k]=max(f[b][j][k],f[a][j-1][k])+1;
				else {
					if(k-1>=0) f[a][j][k]=max(f[b][j][k-1],f[a][j-1][k-1])+1;
					else f[a][j][k]=max(f[b][j][k],f[a][j-1][k]);
				}
			}
		}
	}
	
	printf("%d\n",f[n&1][m][x]);
}   

int main() {
    // init();
    // stin();

    scanf("%d",&T);
    // T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}