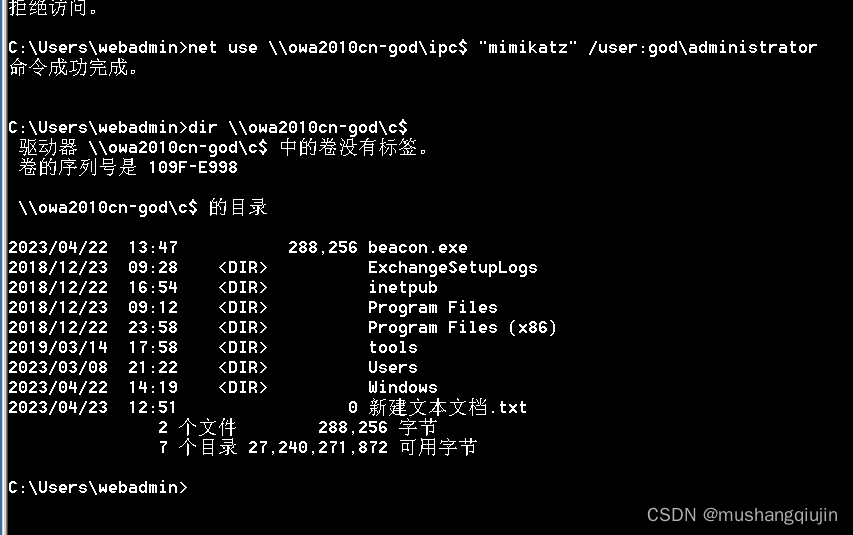
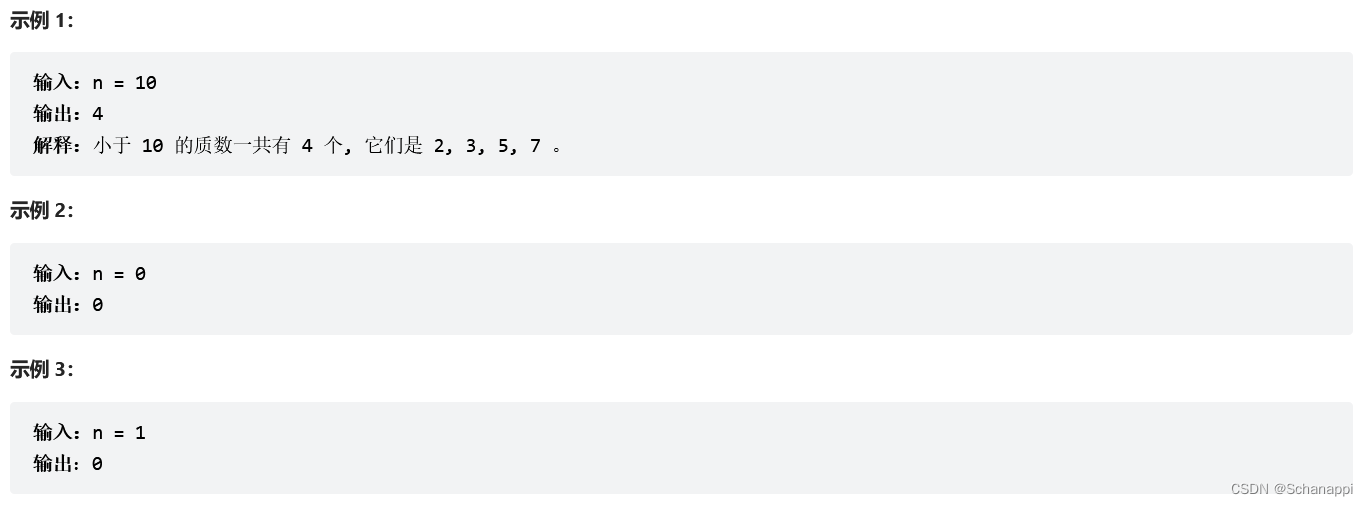
204.计数质数（中等）

在这里插入图片描述

思路

埃拉托斯特斯筛法（简称埃氏筛法），适用于「判断一个整数是否是质数」，该方法可以在判断一个整数 n 时，同时判断所有小于 n 的整数。

从 1 到 n 进行遍历，假设当前遍历的数字为 m，则把所有小于 n 、且是 m 的倍数的整数标记为合数；遍历完成后，没有被标记的数字就是质数。

代码

class Solution {
public:
    int countPrimes(int n) {
        if(n <= 1)  return 0;
        int ans = n - 2; // 1 不是质数，小于n，所以n也不能计入
        vector<bool> prime(n, true); // 是否是质数
        for(int i=2; i<n; ++i){
            if(prime[i]){
                // 考虑i的倍数
                for(int j=2*i; j<n; j+=i){
                    if(prime[j]){
                        // j 是 i 的倍数，因此不是质数
                        prime[j] = false;
                        --ans;
                    }
                }
            }
        }
        return ans;
    }
};

优化

显然，这个算法过于繁琐，有些数字我们很容易就能确定它不是质数，比如偶数一定不是质数，一开始就可以将它们排除。

此外，最小的质因数一定小于被开方数，基于这两个理论，我们可以对算法进行优化。

为什么从x² 开始？

因为计算 i² 之前就计算了 i * 2 ，i * 3 , … , i*(i-1)。

假如我们要判断9是不是质数。如果它不是质数，一定有两个数相乘等于它。这两个因数一定有一个因数小于等于根号9。也就是3。

那么反过来，我们已经把比3小的数的所有的倍数都排除了。

那么对于3到9之间的数，比如7，如果不是质数，它的一个因子应该是小于3。但是小于3的数的所有倍数都被我们排除了。所以当我们验证到3的倍数的时候，最小的倍数就是3的平方。

代码

class Solution {
public:
    int countPrimes(int n) {
        if(n <= 2)  return 0;
        int ans = n/2; // 排除偶数
        vector<bool> prime(n, true); // 是否是质数
        int i = 3, sqrtn = sqrt(n);
        // 最小质因数一定小于等于开方数
        while(i <= sqrtn){
            for(int j=i*i; j<n; j+=2*i){ // 避免偶数和重复遍历
                if(prime[j]){
                    --ans;
                    prime[j] = false;
                }
            }
            do{
                i += 2;
            }while(i <= sqrtn && !prime[i]); // 避免偶数和重复遍历
        }
        return ans;
    }
};