一、ORM框架介绍

ORM框架，把类和数据进行映射，通过类和对象操作它对应表格中的数据，进行增删改查（CRUD)

ORM框架中

数据库：需要提前手动创建数据库

数据表：与OMR框架中的模型类对应

字段：模型类中的类属性（Field子类）

记录：一行数据，多个模型类（字段）的实例。

二、Django配置数据库

2.1 在本地mysql中创建数据库与用户

1、启动本地的mysql

我本地使用的docker ，启动mysql（先启动docker,再启动docker中的myql)

2、在本地mysql中创建数据库与用户

创建my_django的数据库

CREATE DATABASE my_django charset=utf8mb4;

创建用户??

GRANT ALL PRIVILEGES ON *.* TO 'miaojiang'@'%' IDENIFIED BY '123456';

flush privileges; 

2.2 django 连接本地mysql

1、本地安装 mysqlclient

pip install mysqlclient

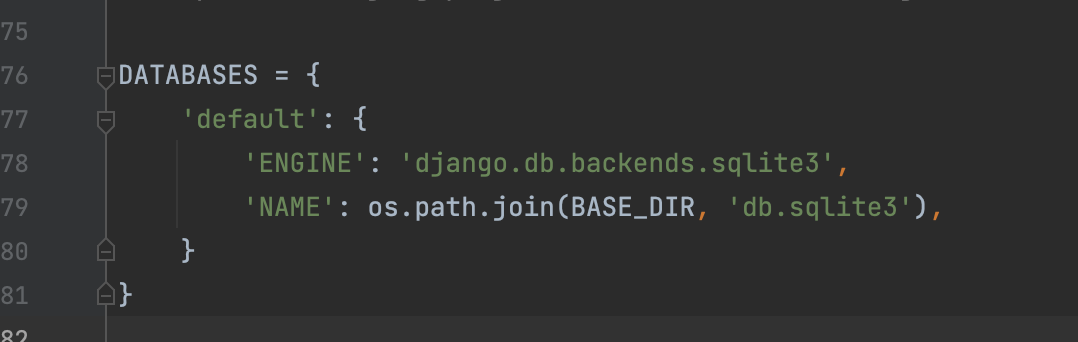
在settings.py 文件中，DATABASES 配置数据库信息