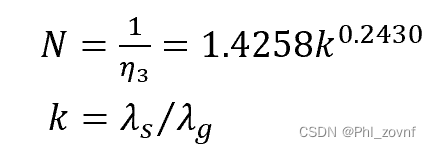前面两篇博客介绍了双层优化的基本原理和使用KKT条件求解双层优化的方法，以及使用yalmip工具箱求解双层优化的方法：

双层优化入门(1)—基本原理与求解方法

双层优化入门(2)—基于yalmip的双层优化求解(附matlab代码)

除了数学规划方法之外，还可采用智能优化算法求解双层优化问题，一般在上层优化中采用智能优化算法，下层优化使用数学规划方法；也可以在上下层优化中都采用智能优化算法，这篇博客将进行详细介绍。

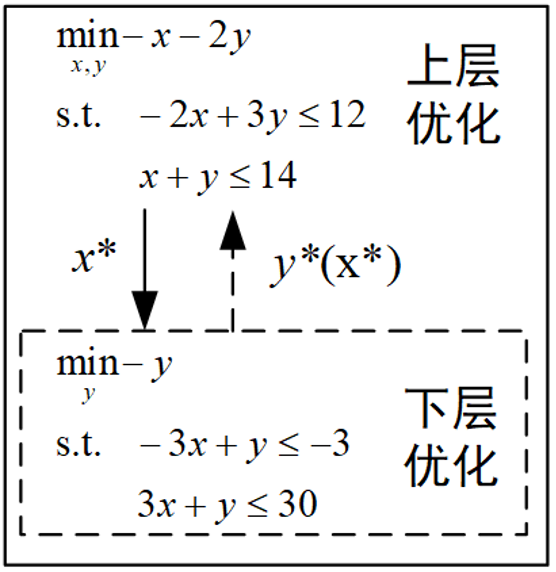
算例依旧使用上面两篇博客中的线性双层优化问题，由于这个优化问题比较简单，我们采用最基础的粒子群算法进行求解。

1.粒子群算法

1995年，受到鸟群觅食行为的规律性启发，James Kennedy和Russell Eberhar建立了一个简化算法模型，经过多年改进最终形成了粒子群优化算法(Particle Swarm Optimization, PSO) ，也可称为粒子群算法。

关于算法的原理及步骤可以参考这篇博客：

粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)

我们假设目标函数是平方和最小，也就是：

假设种群数为200，问题维度为10，最大迭代次数为200，位置上下限分别为10，-10，速度上下限为5，-5，惯性权重取固定值0.9，自我学习因子以及群体学习因子都取1.5，Matlab代码如下：

%% 清除变量
clc
clear
close all
warning off
%% 设置种群参数
sizepop = 200;                      % 初始种群个数
dim = 10;                           % 空间维数
ger = 200;                          % 最大迭代次数    
x_max = 10*ones(1,dim);             % 位置上限
x_min = -10*ones(1,dim);            % 位置下限
v_max = 5*ones(1,dim);              % 速度上限
v_min = -5*ones(1,dim);             % 速度下限
w=0.9;                              % 惯性权重
c_1 = 1.5;                          % 自我学习因子
c_2 = 1.5;                          % 群体学习因子 
%% 种群初始化
pop=x_min+rand(sizepop,dim).*(x_max-x_min);     % 初始化种群
pop_v=v_min+rand(sizepop,dim).*(v_max-v_min);   % 初始化种群速度        
pop_zbest=pop(1,:);                             % 初始化群体最优位置
pop_gbest=pop;                                  % 初始化个体最优位置
fitness=zeros(1,sizepop);                       % 所有个体的适应度
fitness_zbest=inf;                              % 初始化群体最优适应度
fitness_gbest=inf*ones(1,sizepop);              % 初始化个体最优适应度
% 初始的适应度
for k=1:sizepop
    % 计算适应度值
    fitness(k)=sum(pop(k,:).^2);
    if fitness(k)<fitness_zbest
        fitness_zbest=fitness(k);
        pop_zbest=pop(k,:);
    end
end
history_pso=zeros(1,ger);            % 粒子群历史最优适应度值
%% 迭代求最优解
iter=1;
while iter <= ger
    for k=1:sizepop
        % 更新速度并对速度进行边界处理 
        pop_v(k,:)= w * pop_v(k,:) + c_1*rand*(pop_gbest(k,:)-pop(k,:))+c_2*rand*(pop_zbest-pop(k,:));
        for kk=1:dim
            if  pop_v(k,kk) > v_max(kk)
                pop_v(k,kk) = v_max(kk);
            end
            if  pop_v(k,kk) < v_min(kk)
                pop_v(k,kk) = v_min(kk);
            end
        end
        % 更新位置并对位置进行边界处理
        pop(k,:)=pop(k,:)+pop_v(k,:);
        for kk=1:dim
            if  pop(k,kk) > x_max(kk)
                pop(k,kk) = x_max(kk);
            end
            if  pop(k,kk) < x_min(kk)
                pop(k,kk) = x_min(kk);
            end
        end
        % 更新适应度值
        fitness(k)=sum(pop(k,:).^2);
        if fitness(k)<fitness_zbest
            fitness_zbest=fitness(k);
            pop_zbest=pop(k,:);
        end
        if fitness(k)<fitness_gbest(k)
            fitness_gbest(k)=fitness(k);
            pop_gbest(k,:)=pop(k,:);
        end
    end
    history_pso(iter)=fitness_zbest;
    disp(['PSO第',num2str(iter),'次迭代最优适应度=',num2str(fitness_zbest)])
    iter=iter+1;
end
disp(['最优解：x=',num2str(pop_zbest)])
disp(['最优函数值=',num2str(fitness_zbest)])
plot(history_pso,'linewidth',1)
ylabel('最优适应度值')
xlabel('迭代次数')

运行结果如下：

我们知道最优解是当所有变量都取0时，最优函数值为0，上面显示采用粒子群算法求出的显然并不是全局最优解，只是一个局部最优解。这也是智能优化算法无法避免的问题，即使是一个非常简单的目标函数，求出的结果也无法保证是全局最优，那么当目标函数变复杂时，情况将会更糟糕。现在对智能优化算法的研究非常多，各种动植物园算法、各种改进都层出不穷，但还是无法从根本上解决算法无法保证全局收敛的问题。

所以，只有在数学模型比较复杂，非线性条件很多，而且对结果的误差是可以接受的情况下，才建议使用智能优化算法进行求解。

下面以粒子群算法为例，介绍采用智能优化算法求解双层优化问题的方法。

2.智能优化算法中对约束条件的处理

上面提供的代码中，含有的约束条件是x∈[-10,10]，直接可以通过粒子位置的上下限进行约束，但其他形式的约束就没办法这样处理了，常用的处理方式有三类，以上面提到的双层优化问题的上层优化为例，分别介绍这几种方法：

1）通过加罚函数的方式将有约束的问题转为无约束问题：

首先定义罚函数：

然后将罚函数加入原来的目标函数中形成新的目标函数：

其中，p是惩罚因子。这样处理，可以使得违反约束的粒子目标函数值变得很大，从而促使粒子朝着遵守约束的区域聚集。这种方式在过去非常常用，但我自己不太喜欢这种方式，原因待会我会解释。假设惩罚因子为1，新的目标函数可以用matlab代码表示出来：

function fitness=fitness_fun_method1(pop)
    x=pop(1);
    y=pop(2);
    punish=0;
    p=1;
    if -2*x+3*y > 12
        punish=punish+p*(-2*x+3*y-12);
    end
    if x+y > 14
        punish=punish+p*(x+y-14);
    end
    fitness=-x-2*y+punish;
end

运行结果如下：

很奇怪的是，明明最优解是x=6,y=8,最优函数值是-22，但求出的结果却完全不一样，甚至是违反约束条件的。

这就是罚函数的缺点，因为你把约束条件当作罚函数加进目标函数里，当惩罚因子选的不合适时，实际上是改变了目标，很有可能导致最优解和最优函数值都发生了变化，和你原来的目标背道而驰了。解决的办法就是要选择一个合适的惩罚因此，比如我改成9，再重新求解：

这时候得到的结果就是正常的了。

但说实话，我在运行之前也不知道我滴惩罚因子到底多大合适，如果要求解的问题比较复杂，运行时间很长，可能一个错误的惩罚因子就能让你白忙活半天。所以我不太喜欢这种方式。

2）当约束被违反时，给这个粒子赋一个很差的适应度值；

第二种方式说起来就很简单，就是让违反约束的粒子适应度很差。如果是最小化问题就给他赋一个很大的值，如果是最大化问题就赋一个很小的值。这时候目标函数Matlab代码可以这样写：

function fitness=fitness_fun_method2(pop)
    x=pop(1);
    y=pop(2);
    if -2*x+3*y > 12
        fitness=999;
    end
    if x+y > 14
        fitness=999;
    end
    if -2*x+3*y <= 12 && x+y <= 14
        fitness=-x-2*y;
    end
end

运行时可以求出最优解：

3）初始化粒子时，仅产生满足约束条件的粒子，当约束被违反时，重新生成一个满足约束的粒子。

这种方式和其他两种方式的角度不同，是从粒子的初始化和更新的角度进行考虑，而不是从适应度函数的角度出发。

首先，在初始化种群时，保证生成的粒子都是满足约束条件的，可以采用下面的代码：

while true
    pop0=x_min+rand(sizepop*10,dim).*(x_max-x_min);
    x = pop0(:,1);
    y = pop0(:,2);
    % 使用逐元素运算检查约束条件
    mask = (-2*x+3*y<=12) & (x+y<=14) ;
    % 如果点的数量已经足够了，则退出循环
    if nnz(mask) >= sizepop
        pop=[x(mask), y(mask)];
        break;
    end
end
pop=pop(1:sizepop,:);                           % 初始化种群

目标函数可以不考虑任何约束条件：

function fitness=fitness_fun_method3(pop)
    x=pop(1);
    y=pop(2);
    fitness=-x-2*y;
end

但是当更新粒子之后如果不满足约束条件，需要将该粒子修复为满足约束的粒子：

% 更新位置并对位置进行边界处理
pop(k,:)=pop(k,:)+pop_v(k,:);
x=pop(k,1);
y=pop(k,2);
% 修复不满足约束的粒子
if (-2*x+3*y > 12 )|| (x+y > 14)
    while true
        pop0=x_min+rand(10,dim).*(x_max-x_min);
        x = pop0(:,1);
        y = pop0(:,2);
        % 使用逐元素运算检查约束条件
        mask = (-2*x+3*y<=12) & (x+y<=14) ;
        % 如果数量已经足够了，则退出循环
        if nnz(mask) >= 1
            pop_test=[x(mask), y(mask)];
            pop(k,:)=pop_test(1,:);
            break;
        end
    end
end

优化结果如下：

我们可以看到，在初始化种群以及更新粒子时都考虑约束条件时，也可以求出较优的解。

此外根据所求优化问题的实际情况不同，也可以将上面几种对约束条件的不同处理方式相结合。例如，在初始化以及更新种群时考虑一部分约束，另一部分约束采用罚函数的方式添加到目标函数中，此处不再赘述。

3.上层优化采用粒子群算法，下层优化使用yalmip或粒子群算法进行求解

对于双层优化的问题求解，第一种方式是上层优化采用智能优化算法，下层问题使用yalmip等工具箱直接求出最优解。第二种方式是上下层优化都采用智能优化算法。还是以上面那个线性双层优化问题为例，采用第二种方法处理约束条件，说明一下采用智能优化算法求解双层优化问题的具体步骤：

1)设置算法参数

采用智能优化算法求解上层优化问题时，由于上下层需同时优化，并进行迭代，为避免求解时间过长，种群规模和迭代次数不宜过大，在这里设置为30和50。另外，变量y的取值需要在下层优化中进行决策，上层优化只需要决策变量x，因此上层优化的粒子群算法问题维度设置为1。

%% 设置种群参数
sizepop = 30;                       % 初始种群个数
dim = 1;                            % 空间维数
ger = 50;                           % 最大迭代次数    
x_max = 14*ones(1,dim);             % 位置上限
x_min = zeros(1,dim);               % 位置下限
v_max = 7*ones(1,dim);              % 速度上限
v_min = -7*ones(1,dim);             % 速度下限
w=0.9;                              % 惯性权重
c_1 = 1.5;                          % 自我学习因子
c_2 = 1.5;                          % 群体学习因子

2)初始化种群

%% 种群初始化
pop=x_min+rand(sizepop,dim).*(x_max-x_min);     % 初始化种群
pop_v=v_min+rand(sizepop,dim).*(v_max-v_min);   % 初始化种群速度        
pop_zbest=pop(1,:);                             % 初始化群体最优位置
pop_gbest=pop;                                  % 初始化个体最优位置
fitness=zeros(1,sizepop);                       % 所有个体的适应度
fitness_zbest=inf;                              % 初始化群体最优适应度
fitness_gbest=inf*ones(1,sizepop);              % 初始化个体最优适应度

3)计算种群初始适应度

for k=1:sizepop
    % 计算适应度值
    fitness(k)=up_fitness_fun(pop(k,:));
    if fitness(k)<fitness_zbest
        fitness_zbest=fitness(k);
        pop_zbest=pop(k,:);
    end
end
history_pso=zeros(1,ger);            % 粒子群历史最优适应度值

粒子的适应度函数(也就是优化问题的目标函数取值)取决于变量x和y的值，而y的取值又由下层优化决定，因此求适应度函数的过程其实就是一个迭代过程，上层优化向下层优化传递变量x，下层优化根据x的取值和自身的目标函数以及约束条件，得到y的取值，然后向上层优化传递，最终根据x和y的取值综合得到目标函数，我们这里选择yalmip求解下层优化问题，代码如下：

%% up_fitness_fun.m
function fitness=up_fitness_fun(pop)
    x=pop;
    y=main_down(x);
    punish=0;
    if -2*x+3*y > 12
        punish=punish+999;
    end
    if x+y > 14
        punish=punish+999;
    end
    fitness=-x-2*y+punish;
end
%% main_down.m
function best_y=main_down(x)
    y=sdpvar(1);
    Constraints=[-3*x+y <= -3 , 3*x+y <= 30 ];
    objective=-y;
    ops=sdpsettings('verbose', 0 , 'solver', 'cplex');
    optimize(Constraints,objective,ops);
    best_y=value(y);
end

4)迭代求最优解

最终优化结果如下：

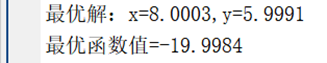
求解结果和前两篇博客都一样(非常接近全局最优解x=8,y=6)，但是因为每次迭代时，每个上层粒子都需要将自身的参数传递给下层粒子求解下层优化问题，意味着完成计算过程需要sizepop×ger=1500次下层优化，所以需要的时间很长。如果问题规模更大，模型更复杂，采用智能优化算法求解双层优化问题所需的时间将会更多，这时候就可以考虑将非线性双层优化问题模型简化为线性双层优化，然后再使用KKT条件转为单层优化问题进行求解。这样求解时间会大大缩短，可能也会提高计算精度（智能优化算法的局部收敛问题）