---

s.substr(n, m) // 从字符串s的索引n开始，向后截取m个字符
例：
string s = "aaabbbcccddd";
string s1 = s.substr(2,3);
此时s1为abb

1 131 分割回文串

切割问题，前文均为组合问题。组合问题与切割问题的区别在于for每层的选择：

例如，对于字符串abcdef：
组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…。
切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…。

随着递归深入for循环，每次截取的字符串长度不同。
此题操作的数组也很关键
vector<string> path
vector<vector<string>> res

1、返回条件
回溯作为深度优先遍历，每次都会线递归到最深处，然后在回溯到for的i++
而返回条件为到达递归的最深处才返回，此时的path可能已经包含了不止一个回文串了（每次进入新的for中都有可能有回文串加入path）

if(startIndex == s.size()){
	res.push_back(path);
	return;
}

2、单层for循环条件
如何截取子串？for (int i = startIndex; i < s.size(); i++)循环中， [startIndex, i] 这个区间就是截取的子串。
startIndex一定需要，记录下一层递归分割的起始位置。

for (int i = startIndex; i < s.size(); i++) {
    if (判断输入字符串s从startIndex到i的部分是不是回文子串) { // 是回文子串 isPalindrome(s, startIndex, i)
        // 获取[startIndex,i]在s中的子串
        string str = s.substr(startIndex, i - startIndex + 1);
        path.push_back(str);
    } else {                // 如果不是则直接跳过
        continue;
    }
    dfs(s, i + 1); // 寻找i+1为起始位置的子串
    path.pop_back();        // 回溯过程，弹出本次已经填在的子串
}

判断是否是回文串isPalindrome函数：双指针

 bool isPalindrome(const string& s, int start, int end) {
     for (int i = start, j = end; i < j; i++, j--) {
         if (s[i] != s[j]) {
             return false;
         }
     }
     return true;
 }

3、输入
void dfs(string s, int startIndex)

2 93 复原 IP 地址

此题与1题为同类型题

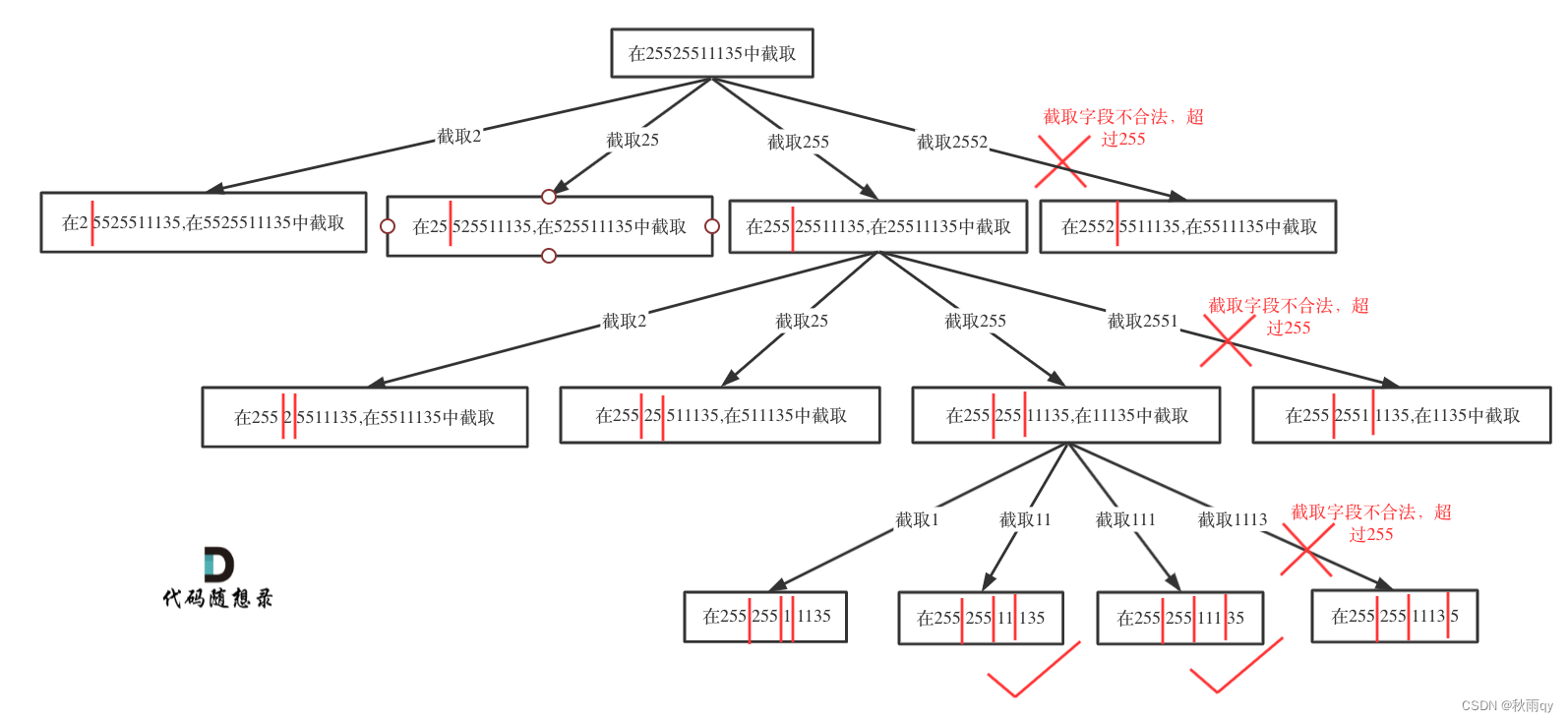
0、此题输入为
void dfs(string& s, int startIndex, int pointNum)
其中会原地修改字符串s（加入.），startIndex需要+2，pointNum记录.的数量。

使用vector<string> result记录结果。
其中塞入的是原地修改的输出字符串s
1、返回条件
终止条件和题1情况不同，本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，以分割的段数作为终止条件。
故使用逗号数量来判断。pointNum表示逗点数量，pointNum为3说明字符串分成了4段了。

然后验证一下第四段是否合法，如果合法就加入到结果集里。

if (pointNum == 3) { // 逗点数量为3时，分隔结束
    // 判断第四段子字符串是否合法，如果合法就放进result中
    if (isValid(s, startIndex, s.size() - 1)) {
        result.push_back(s);
    }
    return;
}

2、单层for循环逻辑

如题1相同，for (int i = startIndex; i < s.size(); i++)循环中， [startIndex, i]这个区间就是截取的子串，需要一个isValid()函数判断这个子串是否合法。
如果合法就在字符串后面加上符号.表示已经分割。
如果不合法就结束本层循环，如图中剪掉的分支：

递归和回溯：
递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointNum 要 +1。
回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。

for (int i = startIndex; i < s.size(); i++) {
    if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
        s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一个逗点
        pointNum++;
        dfs(s, i + 2, pointNum);   // 插入逗点之后下一个子串的起始位置为i+2
        pointNum--;                         // 回溯
        s.erase(s.begin() + i + 1);         // 回溯删掉逗点
    } else break; // 不合法，直接结束本层循环
}

判断子串是否合法
考虑到如下三点：

1 段位以0为开头的数字不合法
2 段位里有非正整数字符不合法
3 段位如果大于255了不合法

// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法
bool isValid(const string& s, int start, int end) {
    if (start > end) {
        return false;
    }
    if (s[start] == '0' && start != end) { // 只有一位且以0开头的数字不合法
            return false;
    }
    int num = 0;
    for (int i = start; i <= end; i++) {
        if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
            return false;
        }
        num = num * 10 + (s[i] - '0');
        if (num > 255) { // 如果大于255了不合法
            return false;
        }
    }
    return true;
}