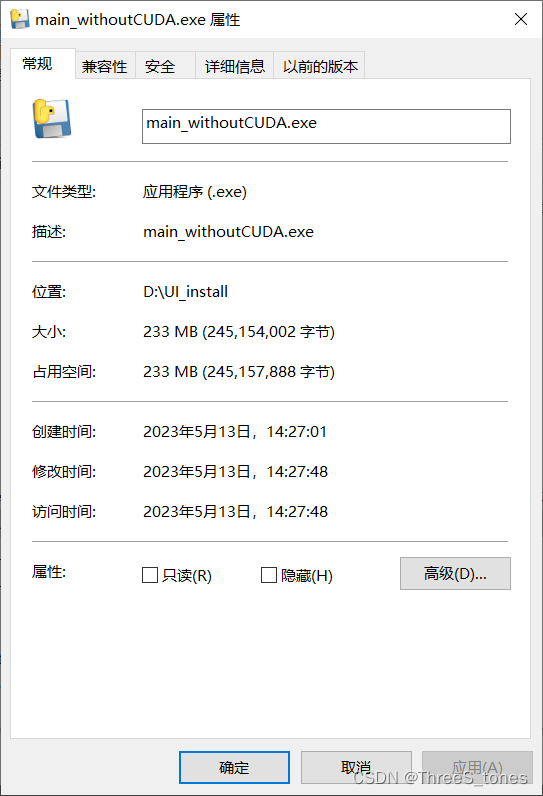
问题一：.exe文件过大

打包命令：

pyinsatller -F -w main.py

解决方法：
新建了一个虚拟环境，在其中重新安装了所需的库。

安装虚拟环境依赖包：

pip install virtualenv
pip install virtualenvwrapper-win

找到自己python.exe所在位置，创建虚拟环境

mkvirtualenv -p="E:\\Python\python.exe" pyinenv

在需要打包的文件目录上输入cmd，使用如下命令切换到虚拟环境中

workon pyinenv

使用命令python main.py运行要打包的主程序，根据弹出缺少的模块依次下载。
注意：需要重新安装pyqt5和pyqt5-tools，以及pyinstaller等，这些运行过程中不会报错。

在下载的时候发现torch里面的cuda占的内存很大，索性在代码中取消了使用cuda加速的部分，并把torch-cuda删除，重新下了个没有cuda的torch、torchvision等

参考：解决打包exe文件过大问题

问题二：pyinstaller与opencv-python版本不兼容

打包完成后出现下面窗口。
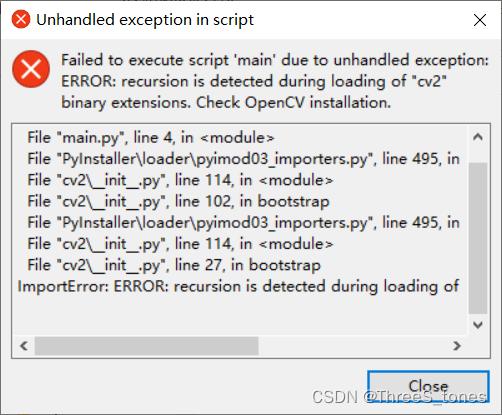
在这里插入图片描述
解决：修改opencv-python的版本pip install opencv-python==4.5.1.48
我是用的python和pyinstaller的版本如下：

PyInstaller: 5.1
Python: 3.9.0
opencv-python：4.5.1.48

问题三：打开文件时提示***.pyd文件已存在

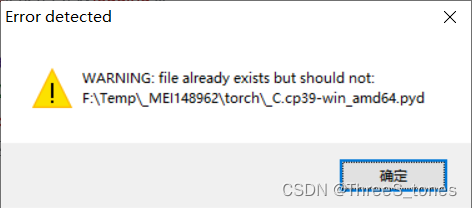
在这里插入图片描述
在a和p之间加入下面代码：

for b in a.binaries.copy():  # Traver the binaries.
    for d in a.datas:  #  Traverse the datas.
        if b[1].endswith(d[0]):  # If duplicate found.
            a.binaries.remove(b)  # Remove the duplicate.
            break

操作完之后换成这个打包命令：

pyinstaller main.spec

参考：Pyinstaller --onefile warning file already exists but should not
参考：WARNING: file already exists but should not: C:\Users\workAI\AppData\Local\Temp_MEI132522\torch_C
参考：【Python】Python打包exe报错makespec options not valid when a.spec file is given

问题四：pyinstaller打包时提示UPX is not available.

解决：
(1) 到官网 https://upx.github.io/ 下载了UPX(我的是Window 64版本), 下载下来是一个压缩包

(2) 解压得到 upx.exe文件

(3) 把exe文件拷贝到pyinstaller.exe目录下, 我的是 C:\Users\HASEE\Envs\pyinenv\Scripts

参考：pyinstaller打包时提示UPX is not available

最终，打包完成并能成功使用。（打包过程用了4分钟左右）
在这里插入图片描述

另：查看CUDA成功配置的方法

（1）在cmd里，注意是配置cuda的环境，我这里是在pytorch环境中，所以要先激活pytorch环境。
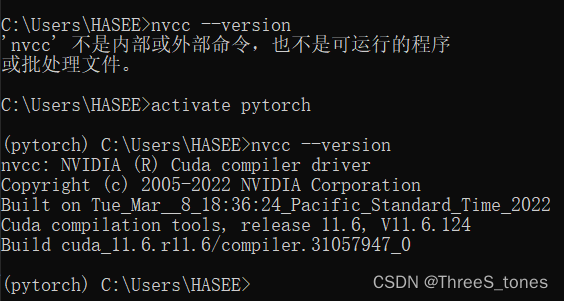
在这里插入图片描述
（2）在python文件中输入

import torch
print(torch.cuda.is_available())

返回True说明配置好了。

之前安装CUDA和pytorch的参考
参考：
1：CUDA版本与显卡驱动版本对照表（更新至2022.10.26 - CUDA11.8）
2：查看已经安装的CUDA的版本
3：win10+Anaconda+pytorch+CUDA11.1 详细安装指南
4：【Pytorch】pytorch安装（包含cuda详细安装教程）

$y_{i,j}=\sum_{m=0}^{h-1}\sum_{n=0}^{w-1}\sum_{k=0}^{c-1}w_{m,n,k}x_{i+m,j+n,k}+b$