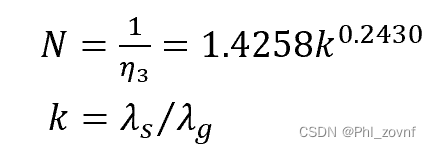区间预测 | MATLAB实现QRCNN-GRU卷积门控循环单元分位数回归时间序列区间预测

news2025/2/23 6:13:52

区间预测 | MATLAB实现QRCNN-GRU卷积门控循环单元分位数回归时间序列区间预测

效果一览

基本介绍

1.Matlab实现基于QRCNN-GRU分位数回归卷积门控循环单元的时间序列区间预测模型；
2.多图输出、多指标输出(MAE、RMSE、MSE、R2)，多输入单输出，含不同置信区间图、概率密度图；
3.data为数据集，功率数据集，用过去一段时间的变量，预测目标，目标为最后一列，也可适用于负荷预测、风速预测；MainQRCNN_GRUTS为主程序，其余为函数文件，无需运行；
4.代码质量高，注释清楚，含数据预处理部分，处理缺失值，如果为nan，用上一行替代，也含核密度估计；

模型描述

QRCNN-GRU是一种神经网络模型，主要用于时间序列区间预测任务。它的全称为Quantile Regression Convolutional Gated Recurrent Unit，其中包含了卷积、门控循环单元和分位数回归等技术。
卷积层用于提取时间序列中的局部特征，门控循环单元则用于捕捉序列之间的长期依赖关系，分位数回归则用于估计预测值的不确定性。这些技术的结合使得QRCNN-GRU能够在时间序列预测中取得较好的效果。
具体而言，QRCNN-GRU首先利用卷积层提取时间序列的局部特征，然后利用门控循环单元对这些特征进行建模，得到一个高维的时间序列表示。接着，QRCNN-GRU使用分位数回归来学习预测值的不确定性，从而得到一个预测值的分布。最后，根据需要，可以利用这个分布来进行区间预测。
总之，QRCNN-GRU利用卷积、门控循环单元和分位数回归等技术，能够有效地处理时间序列数据，并且在时间序列区间预测任务中表现出较好的性能。

QRCNN-GRU的具体公式如下：
首先，输入时间序列 $x_{1:T}$ 经过卷积层得到局部特征表示 $c_{1:T'}$ ：

$c_t = \sum_{i=1}^k w_i x_{t+i-1},\qquad t=1,\ldots,T'$

其中， $k$ 为卷积核大小， $w_i$ 为卷积核参数。
接着，将局部特征表示 $c_{1:T'}$ 输入门控循环单元，得到一个高维的时间序列表示 $h_{1:T''}$ ：

$r_t = \sigma(W_r x_t + U_r h_{t-1} + b_r)$

$z_t = \sigma(W_z x_t + U_z h_{t-1} + b_z)$

$\tilde{h}_t = \tanh(W x_t + U(r_t \odot h_{t-1}) + b)$

$h_t = (1-z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t$

其中， $\sigma$ 为sigmoid函数， $\odot$ 表示逐元素相乘， $W_r$ 、 $U_r$ 、 $b_r$ 、 $W_z$ 、 $U_z$ 、 $b_z$ 、 $W$ 、 $U$ 、 $b$ 分别为门控循环单元的参数。
最后，利用分位数回归来学习预测值的分布 $P(y|x_{1:T})$ ：

$\hat{y}(\tau|x_{1:T}) = f_\tau(h_{T''})$

其中， $\tau$ 为分位数， $f_\tau$ 为分位数回归模型。
根据需要，可以利用预测值的分布 $P(y|x_{1:T})$ 来进行区间预测。例如，对于置信度为 $1-\alpha$ 的区间预测，可以计算 $\hat{y}(\tau_1|x_{1:T})$ 和 $\hat{y}(\tau_2|x_{1:T})$ ，其中 $\tau_1 = \alpha/2$ ， $\tau_2 = 1-\alpha/2$ ，然后得到区间 $[\hat{y}(\tau_1|x_{1:T}), \hat{y}(\tau_2|x_{1:T})]$ 。

程序设计

完整程序和数据获取方式：私信博主。

% 定义QRCNN-GRU模型
num_filters = 16;
kernel_size = 3;
hidden_size = 32;
num_layers = 2;
num_quantiles = 3;
model = qrcnn_gru(num_filters, kernel_size, hidden_size, num_layers, num_quantiles);

% 定义损失函数和优化器
criterion = @(y_pred, y) mean((y_pred - y).^2);
optimizer = @(params, lr) adam(params, lr);

% 训练模型
num_epochs = 100;
batch_size = 32;
lr = 0.001;
params = model.get_params();
for epoch = 1:num_epochs
    for i = 1:num_batches
        x_batch = train_data(i, :, :);
        y_batch = train_labels(i, :);
        y_pred_batch = model.forward(x_batch);
        loss = criterion(y_pred_batch, y_batch);
        grad = model.backward(x_batch, y_pred_batch - y_batch);
        params = optimizer(params, grad, lr);
        model.set_params(params);
    end
end

% 预测
y_pred = model.forward(x_test);
lower = y_pred(:, 1);  % 取第一个分位数
upper = y_pred(:, end);  % 取最后一个分位数

以下是一个基于MATLAB的示例代码，用于实现QRCNN-GRU模型的训练和预测：

% 定义QRCNN-GRU模型
num_filters = 16;
kernel_size = 3;
hidden_size = 32;
num_layers = 2;
num_quantiles = 3;
model = qrcnn_gru(num_filters, kernel_size, hidden_size, num_layers, num_quantiles);

% 定义损失函数和优化器
criterion = @(y_pred, y) mean((y_pred - y).^2);
optimizer = @(params, lr) adam(params, lr);

% 训练模型
num_epochs = 100;
batch_size = 32;
lr = 0.001;
params = model.get_params();
for epoch = 1:num_epochs
    for i = 1:num_batches
        x_batch = train_data(i, :, :);
        y_batch = train_labels(i, :);
        y_pred_batch = model.forward(x_batch);
        loss = criterion(y_pred_batch, y_batch);
        grad = model.backward(x_batch, y_pred_batch - y_batch);
        params = optimizer(params, grad, lr);
        model.set_params(params);
    end
end

% 预测
y_pred = model.forward(x_test);
lower = y_pred(:, 1);  % 取第一个分位数
upper = y_pred(:, end);  % 取最后一个分位数

在这个示例代码中，我们首先定义了一个qrcnn_gru函数，用于构建QRCNN-GRU模型。在训练时，我们使用均方误差作为损失函数，使用Adam优化器进行模型更新。在预测时，我们使用训练好的模型对测试数据进行前向传播，然后根据预测结果得到区间的上下界。
需要注意的是，由于QRCNN-GRU是一种比较新的模型，它的具体实现可能会根据不同的论文和作者有所不同。因此，在实现QRCNN-GRU模型时，需要结合具体的论文和实验结果进行调整和优化。此外，由于MATLAB并不是深度学习领域的主流编程语言，因此在实现QRCNN-GRU模型时可能会受到一定的限制。