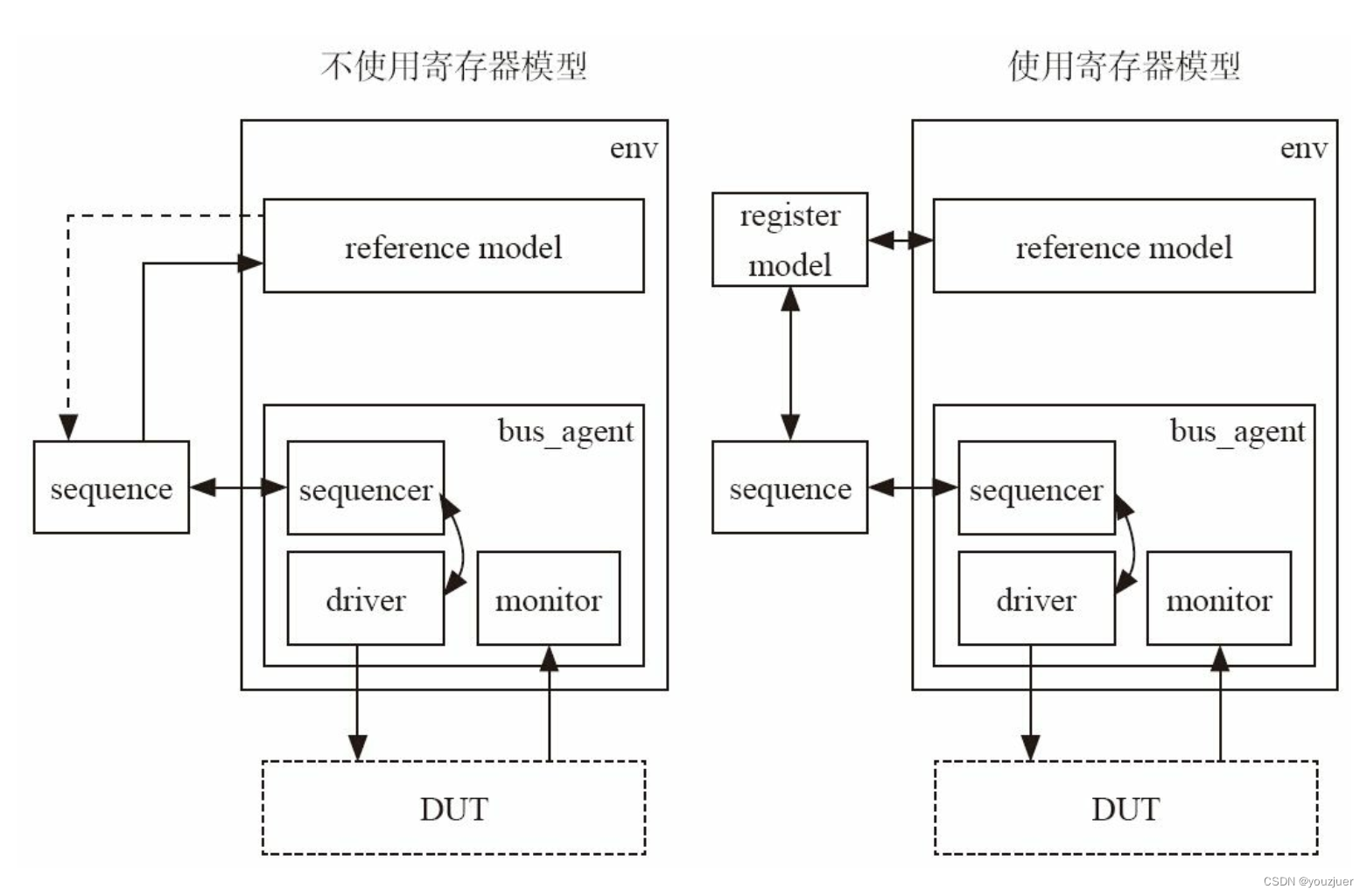
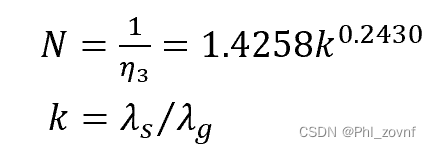最近看到一篇有关“储氢合金/金属氢化物床层有效导热系数的数学模型”的论文,文章DOI:10.1016/j.energy.2023.127085,文章提到的数学物理模型还算好理解一些,特意分享给各位感兴趣的大佬。
一、物理模型简图和假设
文章里,对储氢合金床层作了以下几个假设:
- 金属合金颗粒是球型,储氢合金床层是简单的立方堆积;
- 颗粒之间为点接触;
- 忽略上述点接触的热传导,这是因为真空中床层有效导热系数非常低;
- 传热过程为稳态。
下面是设想的特征单元体,也就是本次文章储氢合金床层的数学模型,其特点就是一个边长为颗粒直径D的立方体中,有两个半径为R的半球形,D=L=2R。通过截面图分析,导热路径经过固体颗粒的路径长度为Ls,经过气体路径长为Lg,Lg+Ls=D=L。
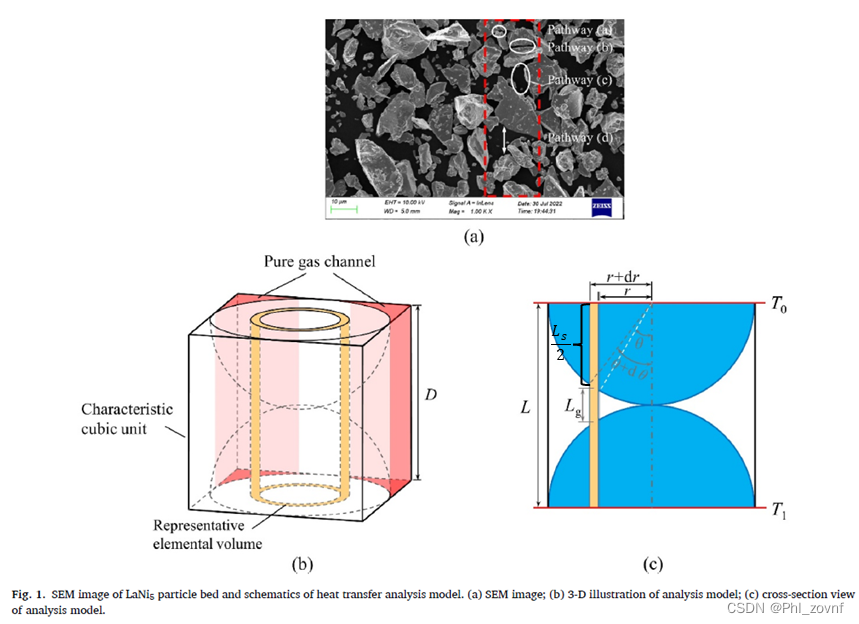
二、一些热流量等物理量的数学推导
根据截面图,通过几何数学关系,得到以下关系,但是根据原文,在算
的时候,本人得不到文章里面的
结果,而是它的倒数
。
由于文章后面很多都是基于
结果展开的,因此先按文章结果来吧。

再根据傅立叶定律,得到以下等式:

通过dФ从0到θ(0≤θ≤π/2)的积分,得到文章里面的等式
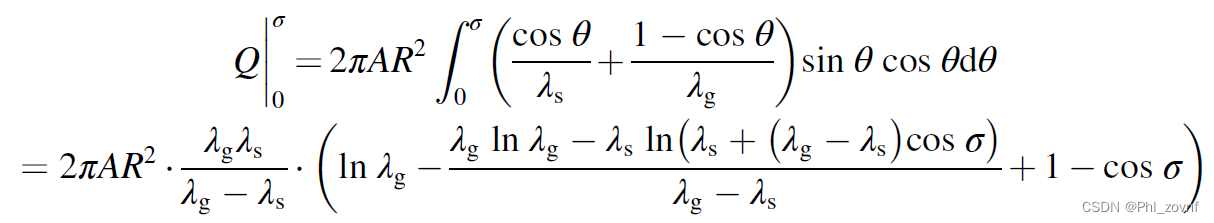
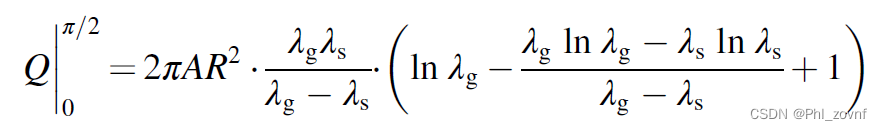
分析纯气体的导热路径,易得以下等式


特征单元体中总的热流量是以下两者的和Qall,并定义η1、η2和η3,η1和η2是超越方程。注意η3中,是指η2=0.9时的有效气体的圆柱体体积/特征单元体总气体体积。
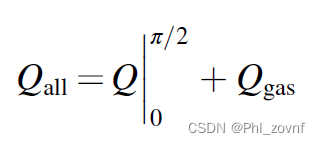
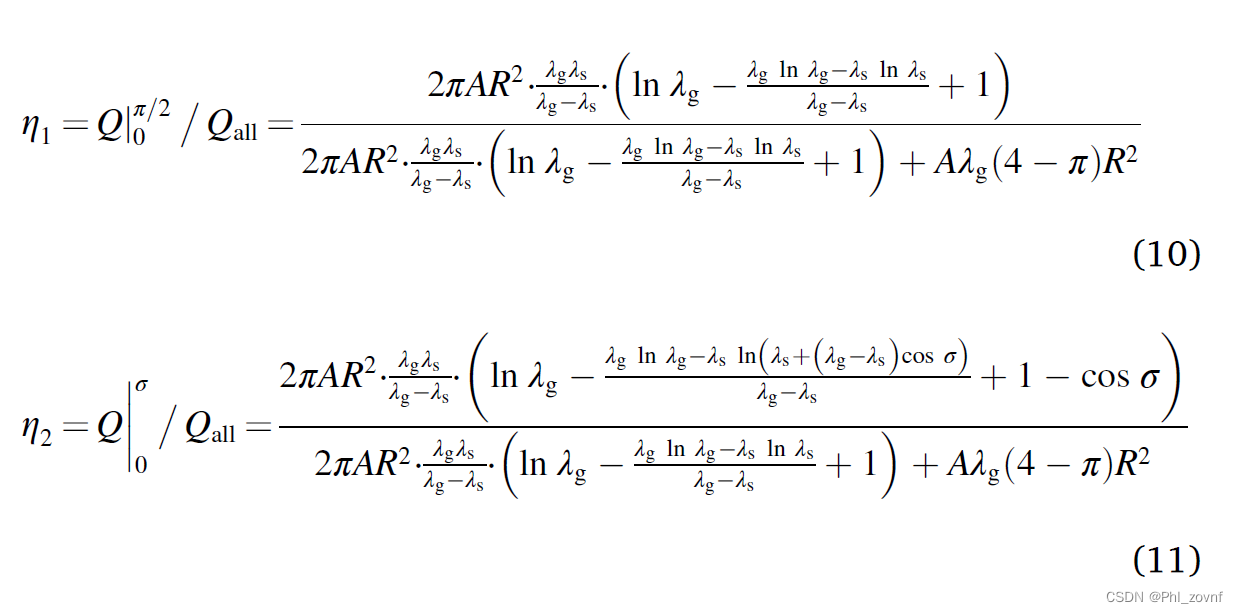
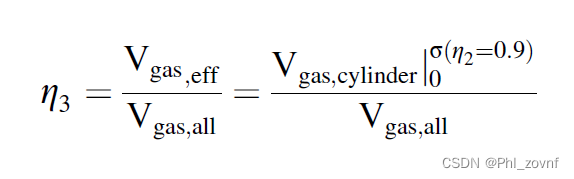
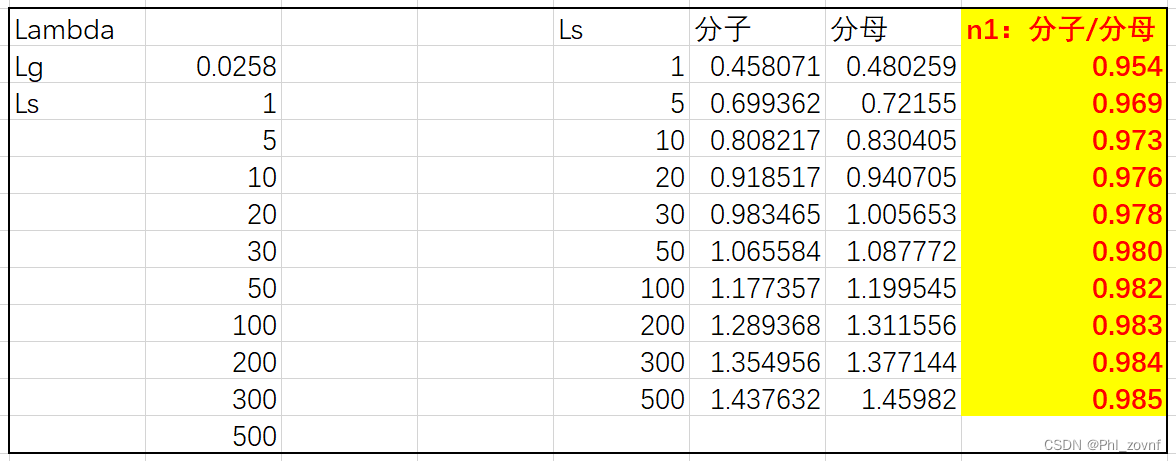
通过带人具体的λs和λg的值,可解出η1的值,在Excel中输入公式,便可获得与文献表格中的η1数据。同时可以看到,η1均大于0.95,由于λs一般都大于1W/(m·K),因此,可以说是等效传热路径中,纯气路传热只占<5%,而95%以上均是“颗粒—气膜——颗粒”路径。

根据文献,η2的公式简化成如下表达式,η2=0.9时,求出θ,得到对应Vgas,eff的值,再用η3的定义式求出η3的值。对于Vgas,eff的几何体积如下,我是圆柱体减去球缺的体积,Vgas,all是正方体减去球型的体积。
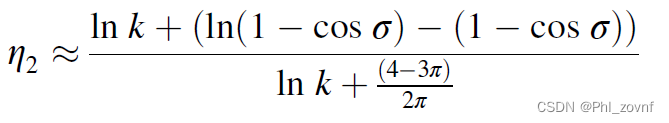

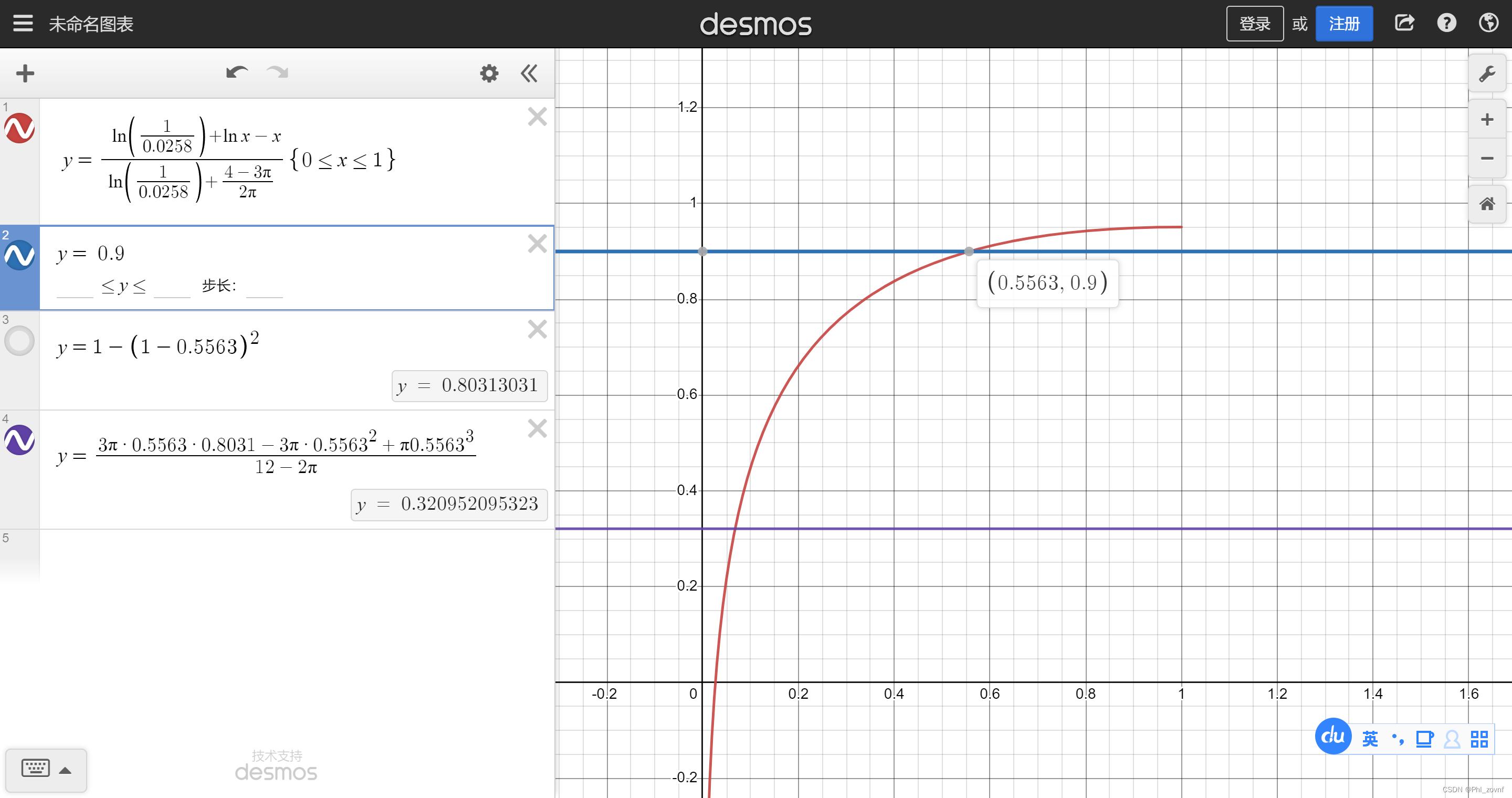
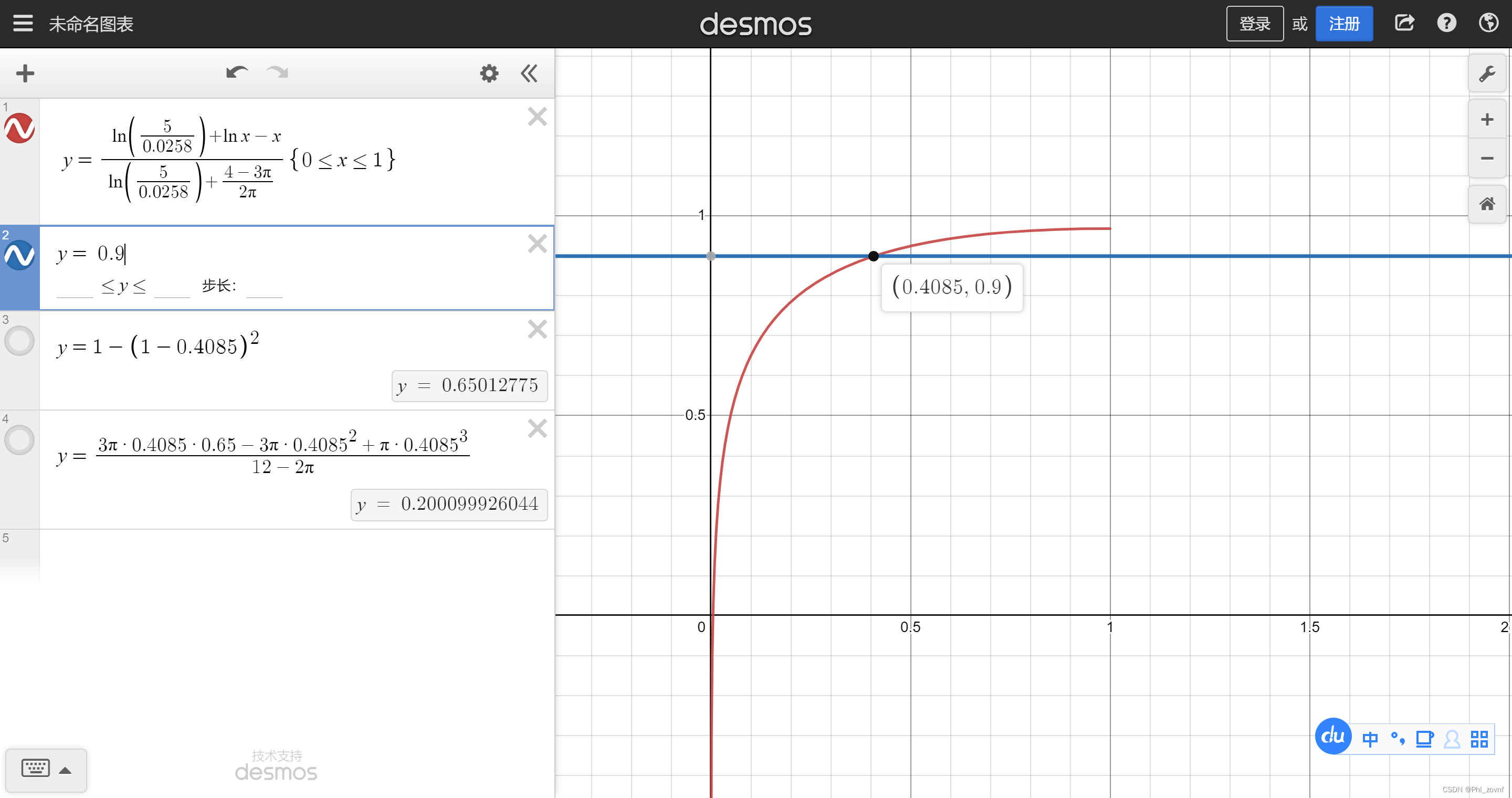
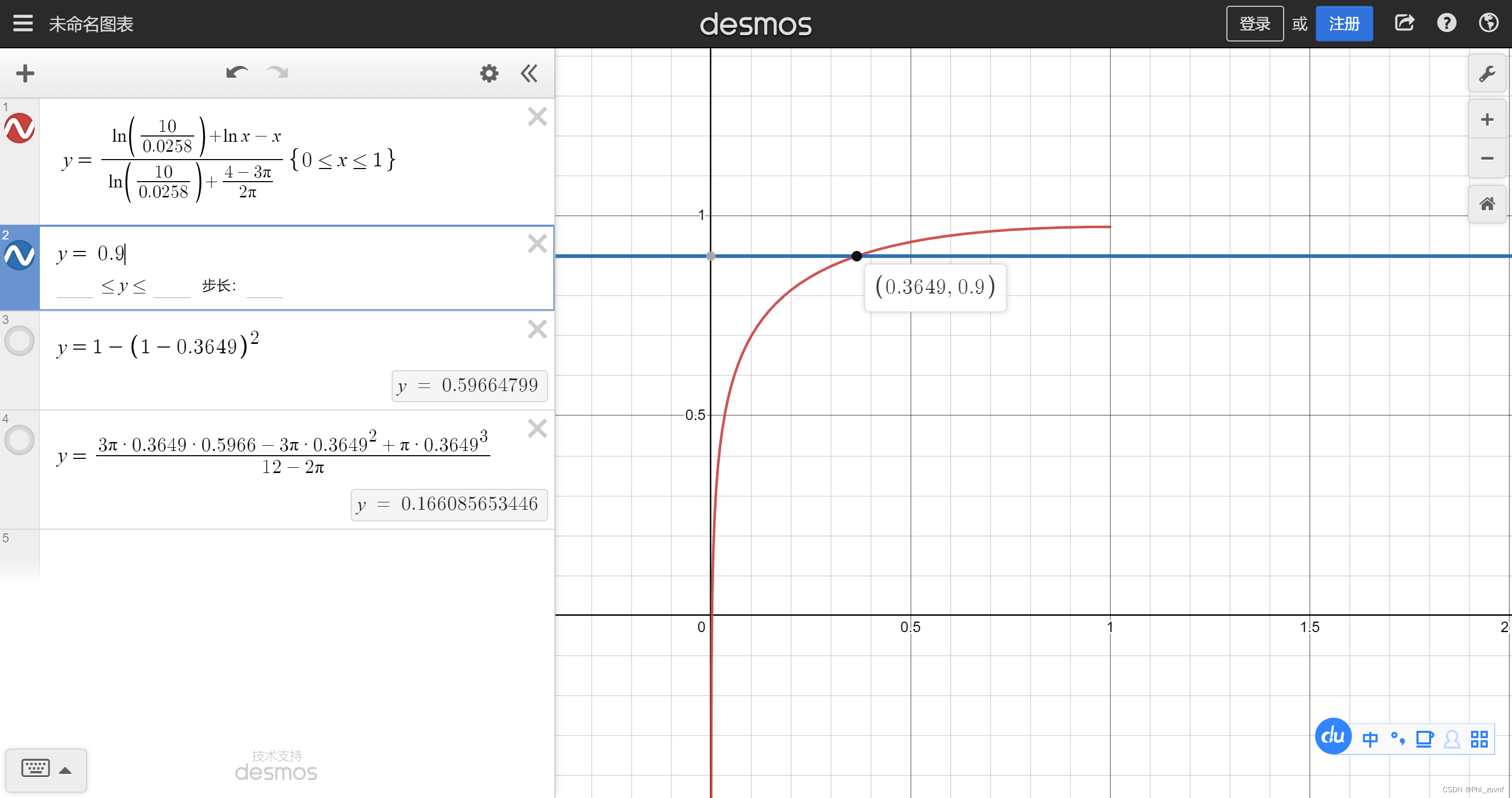
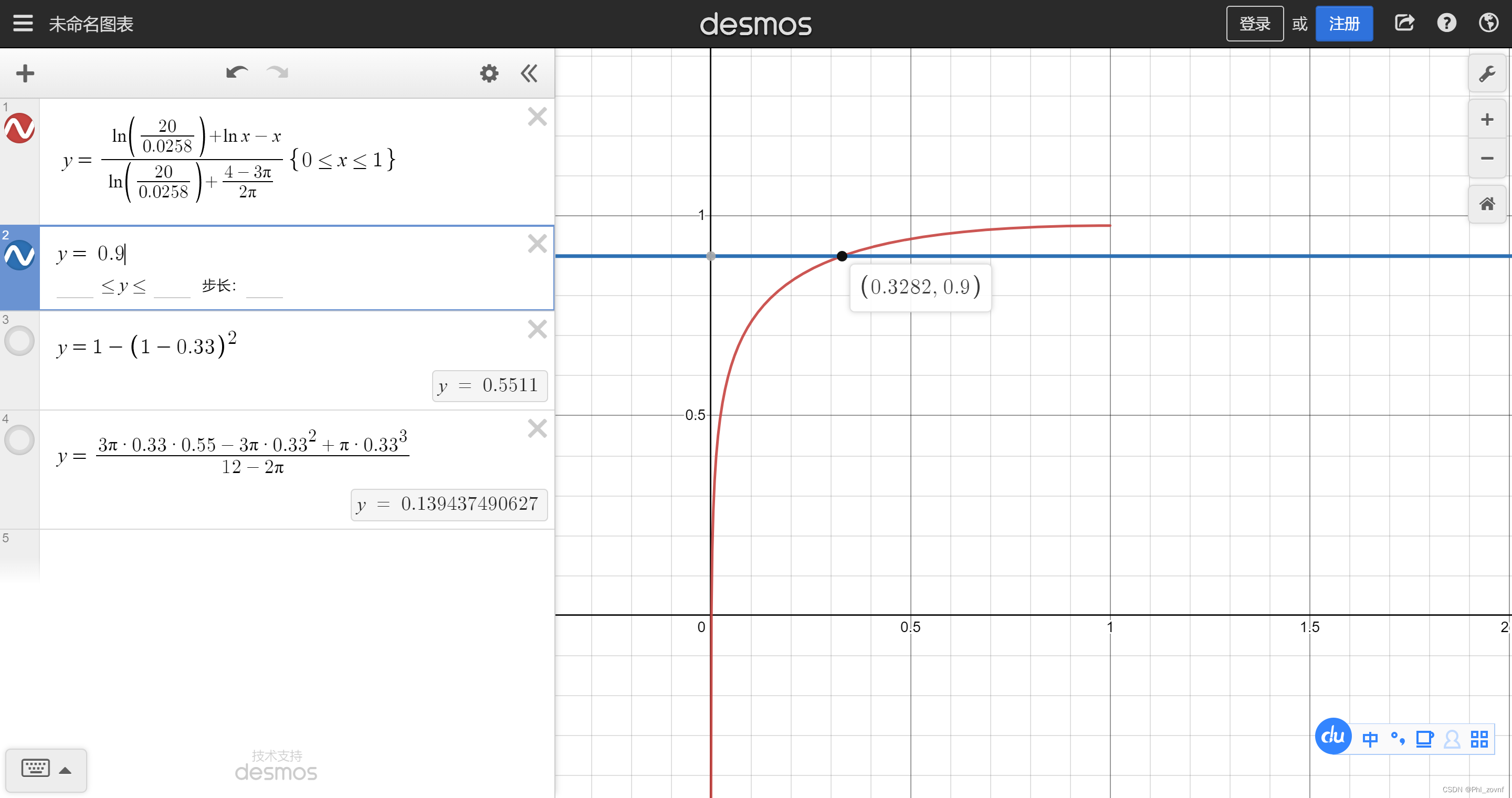
由于本人不太会解lnx-x=C的方程,因此借助数学工具desmos,当η2=0.9,、λs=1,λg=0.0258时,解得1-cosθ=0.5563,(sinθ)^2=1-(1-(1-cosθ))^2=0.80313031。因此得η3=0.321,与文献里表格1的η3=0.306接近,但不相近。我们在算一下 λs=5,λg=0.0258时,η3=2.00,文献η3=1.98; λs=10,λg=0.0258时,η3=0.166,文献η3=1.65; λs=20,λg=0.0258时,η3=0.139,文献η3=1.41。
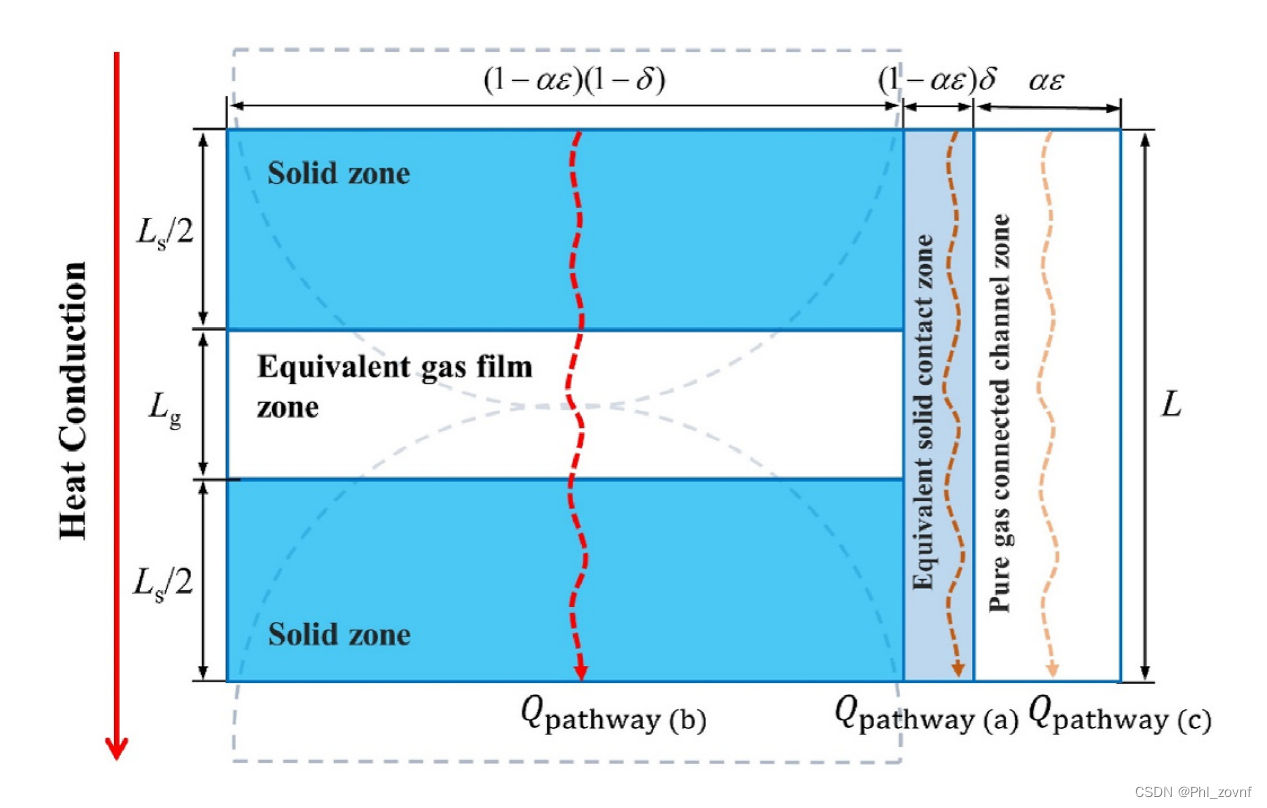
三、等效导热系数的计算
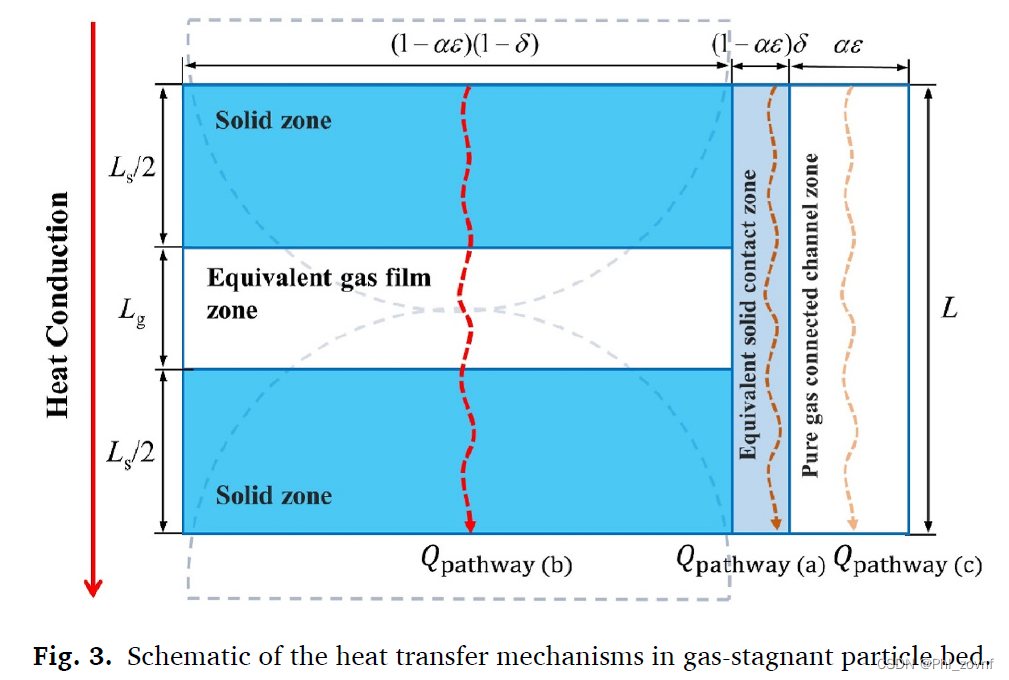
根据上面这个图的分析,有三种导热路径,情况(b)是通过颗粒之间接触的纯颗粒之间导热,情况(a)是“颗粒-气膜-颗粒”路径,根据之前分析,这种情况占据主要地位(>95%),最后的情况(c)是纯气体路径。
热流密度q=λΔT/Δx,假设床层孔隙率为ε,颗粒之间接触比为δ,α为床单元中纯气体占总气体的比例。当接触比为1时,等效导热系数为λs,由于接触比为δ,因此路径体积比为λs*δ,由于孔隙率为ε,即有ε的比例非纯颗粒之间传递热量,又由于ε的比例的体积中,有α比例为纯气体,因此折算有αε为真正纯气体的导热比例,颗粒之间为(1-αε)的比例,所以总的路径体积比为δ*(1-αε),所以情况(b):q_b=λs*δ*(1-αε)*ΔT/L=λs(1-αε)δΔT/L。同理,情况(c):q_c=λg*αε*ΔT/L=λgαεΔT/L。
情况(a)中,根据之前分析,
,因为非接触比为(1-δ),颗粒之间为(1-αε)的比例,所以该情况总的路径体积比为(1-αε)*(1-δ),所以情况(a):q_a=λe*(1-δ)*(1-αε)*ΔT/L=(1-αε)(1-δ)/(Ls/L/λs+Lg/L/λg)ΔT/L。
总热流密度q=q_a+q_b+q_c,根据之前分析,q_a占95%以上,纯气体路径合并到路径(a)中,所以路径(a)的总路径体积比为1-(1-ε)δ,真空中,纯靠颗粒之间导热量很低,推断δ≈0,因此还是得到
,
。
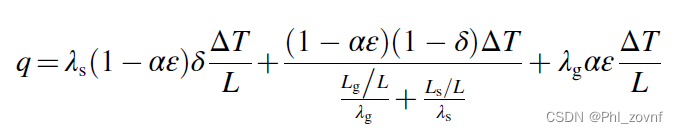
同时,定义N=1/η3,由于Lg'=Lg*η3=Lg/N,L'=Lg'+Ls,ψ'=Lg'/L'=Lg/N/(Lg/N+Ls)=ε/N/(ε/N+(1-ε))

N=1/η3,文献作者通过拟合数据得到以下关系式。因此只需知道孔隙率ε,颗粒导热系数λs,气体导热系数λg,即可得到等效导热系数λe。