半正定Toeplitz矩阵的范德蒙德分解
Toeplitz矩阵的定义:Matrices whose entries are constant along each diagonal are called Toeplitz matrices.
形如
T = [ r 0 r 1 r 2 r 3 r − 1 r 0 r 1 r 2 r − 2 r − 1 r 0 r 1 r − 3 r − 2 r − 1 r 0 ] (1) \boldsymbol{T}=\left[ \begin{matrix} r_0& r_1& r_2& r_3\\ r_{-1}& r_0& r_1& r_2\\ r_{-2}& r_{-1}& r_0& r_1\\ r_{-3}& r_{-2}& r_{-1}& r_0\\ \end{matrix} \right] \tag{1} T=⎣⎢⎢⎡r0r−1r−2r−3r1r0r−1r−2r2r1r0r−1r3r2r1r0⎦⎥⎥⎤(1)
半正定的Toeplitz矩阵:Positive-Semi-Definite Toeplitz, PSD
形如
T = [ r 0 r 1 r 2 r 3 r 1 ∗ r 0 r 1 r 2 r 2 ∗ r 1 ∗ r 0 r 1 r 3 ∗ r 2 ∗ r 1 ∗ r 0 ] , T ≽ 0 (2) \boldsymbol{T}=\left[ \begin{matrix} r_0& r_1& r_2& r_3\\ r_{1}^{*}& r_0& r_1& r_2\\ r_{2}^{*}& r_{1}^{*}& r_0& r_1\\ r_{3}^{*}& r_{2}^{*}& r_{1}^{*}& r_0\\ \end{matrix} \right] , \ \ \ \boldsymbol{T} \succcurlyeq \boldsymbol 0 \tag{2} T=⎣⎢⎢⎡r0r1∗r2∗r3∗r1r0r1∗r2∗r2r1r0r1∗r3r2r1r0⎦⎥⎥⎤, T≽0(2)
其中 T ≽ 0 \boldsymbol{T} \succcurlyeq \boldsymbol 0 T≽0表示 T \boldsymbol{T} T是半正定矩阵。
定理:半正定Toeplitz矩阵的范德蒙德分解
Any PSD Toeplitz matrix T ( u ) ∈ C N × N \boldsymbol T(\boldsymbol u) \in \mathbb C^{N \times N} T(u)∈CN×N of rank r ≤ N r \leq N r≤N admits the following r-atomic Vandermonde decomposition:
T = ∑ k = 1 r p k a ( f k ) a H ( f k ) = A ( f ) d i a g ( p ) A H ( f ) (3) \boldsymbol T = \sum_{k=1}^r p_k \boldsymbol a (f_k) \boldsymbol a^H(f_k) = \boldsymbol A( \boldsymbol f ) diag(\boldsymbol p) \boldsymbol A^H( \boldsymbol f ) \tag{3} T=k=1∑rpka(fk)aH(fk)=A(f)diag(p)AH(f)(3)
where p k > 0 p_k >0 pk>0, and f k ∈ T f_k \in \mathbb T fk∈T, T = ( − 1 2 , 1 2 ] \mathbb T=(-\frac{1}{2}, \frac{1}{2}] T=(−21,21], k = 1 , 2 , ⋯ , r k=1,2,\cdots,r k=1,2,⋯,r are distinct. Moreover, the decompostion above is unique if r < N r < N r<N.
其中
a ( f ) = [ 1 , e i 2 π f , ⋯ , e i 2 π ( N − 1 ) f ] T ∈ C N × 1 \boldsymbol a(f) = [1, e^{i 2 \pi f}, \cdots, e^{i 2 \pi (N-1) f} ]^T \in \mathbb C^{N \times 1} a(f)=[1,ei2πf,⋯,ei2π(N−1)f]T∈CN×1
证明:
(1)首先考虑
r
=
rank
(
T
)
≤
N
−
1
r=\text{rank}(\boldsymbol T) \leq N - 1
r=rank(T)≤N−1的情况
因为
T
≽
0
\boldsymbol T \succcurlyeq 0
T≽0,因此存在
V
∈
C
N
×
r
\boldsymbol V \in \mathbb C^{N \times r}
V∈CN×r满足:
T
=
V
V
H
\boldsymbol T= \boldsymbol {VV}^H
T=VVH。
令
V
−
N
\boldsymbol V_{-N}
V−N为
V
\boldsymbol V
V去掉第
N
N
N行(最后一行)的矩阵:
V
−
N
∈
C
(
N
−
1
)
×
r
\boldsymbol V_{-N} \in \mathbb{C}^{(N-1) \times r}
V−N∈C(N−1)×r,
令
V
−
1
\boldsymbol V_{-1}
V−1为
V
\boldsymbol V
V去掉第
1
1
1行(第一行)的矩阵:
V
−
1
∈
C
(
N
−
1
)
×
r
\boldsymbol V_{-1} \in \mathbb{C}^{(N-1) \times r}
V−1∈C(N−1)×r
因为半正定Toeplitz矩阵的特殊结构,必然有:
V
−
N
V
−
N
H
=
V
−
1
V
−
1
H
\boldsymbol V_{-N} \boldsymbol V^H_{-N}=\boldsymbol V_{-1} \boldsymbol V^H_{-1}
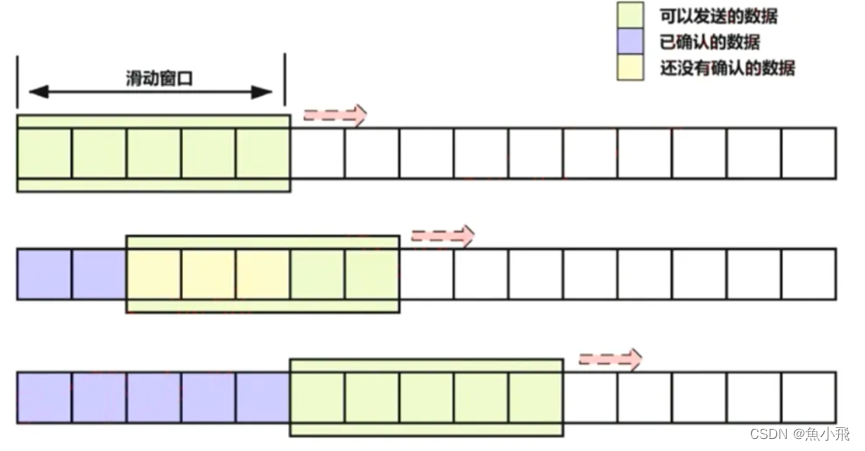
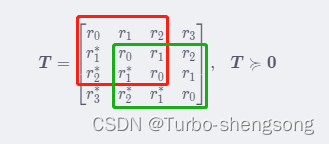
V−NV−NH=V−1V−1H (下图给了一个直观解释,
V
−
N
V
−
N
H
\boldsymbol V_{-N} \boldsymbol V^H_{-N}
V−NV−NH对应红色方框中的矩阵,
V
−
1
V
−
1
H
\boldsymbol V_{-1} \boldsymbol V^H_{-1}
V−1V−1H对应绿色方框中的矩阵,两者是一样的)
因此,一定存在某个酉阵
Q
∈
C
r
×
r
\boldsymbol Q \in \mathbb C^{r \times r}
Q∈Cr×r,使得
V
−
1
=
V
−
N
Q
\boldsymbol V_{-1} = \boldsymbol V_{-N} \boldsymbol Q
V−1=V−NQ,据此我们可以进一步得到(=> it follows that)
V
j
,
:
=
V
1
,
:
Q
j
−
1
,
j
=
2
,
⋯
,
N
\boldsymbol V_{j,:}=\boldsymbol V_{1,:} \boldsymbol Q^{j-1},j=2,\cdots,N
Vj,:=V1,:Qj−1,j=2,⋯,N,因此
u
j
=
V
1
,
:
(
V
j
,
:
)
T
=
V
1
,
:
(
Q
j
−
1
)
H
(
V
1
,
:
)
H
=
V
1
,
:
Q
1
−
j
(
V
1
,
:
)
H
(4)
\begin{aligned} u_j &= \boldsymbol V_{1,:} (\boldsymbol V_{j,:}) ^T \\ &= \boldsymbol V_{1,:} (\boldsymbol Q^{j-1})^H (\boldsymbol V_{1,:})^H \\ &= \boldsymbol V_{1,:} \boldsymbol Q^{1-j} (\boldsymbol V_{1,:})^H \end{aligned} \tag{4}
uj=V1,:(Vj,:)T=V1,:(Qj−1)H(V1,:)H=V1,:Q1−j(V1,:)H(4)
我们可以将
Q
∈
C
r
×
r
\boldsymbol Q \in \mathbb C^{r \times r}
Q∈Cr×r特征分解为(注意
Q
\boldsymbol Q
Q是酉阵,特征分解必然存在):
Q
=
Q
~
d
i
a
g
(
z
1
,
z
2
,
⋯
,
z
r
)
Q
~
H
(5)
\boldsymbol Q = \tilde{\boldsymbol Q} diag(z_1, z_2, \cdots, z_r) \tilde{\boldsymbol Q}^H \tag{5}
Q=Q~diag(z1,z2,⋯,zr)Q~H(5)
其中
Q
~
∈
C
r
×
r
\tilde{\boldsymbol Q} \in \mathbb C^{r \times r}
Q~∈Cr×r是酉阵。因为酉阵的特征值的模都等于1,因此我们可以找到
f
k
∈
T
,
k
=
1
,
2
,
⋯
,
r
f_k \in \mathbb T, k= 1,2,\cdots,r
fk∈T,k=1,2,⋯,r满足
z
k
=
e
i
2
π
f
k
,
k
=
1
,
2
,
⋯
,
r
z_k=e^{i 2 \pi f_k}, k=1,2,\cdots,r
zk=ei2πfk,k=1,2,⋯,r。令
p
k
=
∣
V
1
,
:
Q
~
:
,
k
∣
2
>
0
,
k
=
1
,
⋯
,
r
p_k = \vert \boldsymbol V_{1,:} \tilde{\boldsymbol Q}_{:,k} \vert^2 > 0, k =1,\cdots,r
pk=∣V1,:Q~:,k∣2>0,k=1,⋯,r,将式(5)代入式(4),我们得到
u
j
=
V
1
,
:
Q
~
d
i
a
g
(
z
1
,
z
2
,
⋯
,
z
r
)
1
−
j
Q
~
H
(
V
1
,
:
)
H
=
∑
k
=
1
r
p
k
z
k
1
−
j
=
∑
k
=
1
r
p
k
e
−
i
2
π
(
j
−
1
)
f
k
(6)
\begin{aligned} u_j &= \boldsymbol V_{1,:} \tilde{\boldsymbol Q} diag(z_1, z_2, \cdots, z_r)^{1-j} \tilde{\boldsymbol Q}^H (\boldsymbol V_{1,:})^H \\ &= \sum_{k=1}^r p_k z_k^{1-j} \\ &= \sum_{k=1}^r p_k e^{-i 2 \pi (j-1) f_k} \end{aligned} \tag{6}
uj=V1,:Q~diag(z1,z2,⋯,zr)1−jQ~H(V1,:)H=k=1∑rpkzk1−j=k=1∑rpke−i2π(j−1)fk(6)
由此可以得出式(3)是成立的。另外, f k 1 ≠ f k 2 , k 1 ≠ k 2 f_{k_1} \neq f_{k_2}, k_1 \neq k_2 fk1=fk2,k1=k2,否则 rank ( T ) < r \text{rank}(\boldsymbol T) < r rank(T)<r(与假设矛盾)。
(2)然后考虑
r
=
rank
(
T
)
=
N
r=\text{rank}(\boldsymbol T) = N
r=rank(T)=N的情况
这时,
T
≻
0
\boldsymbol T \succ 0
T≻0。我们随机地选
f
N
∈
T
f_N \in \mathbb T
fN∈T,并且令
p
N
=
(
a
H
(
f
N
)
T
−
1
a
(
f
N
)
)
p_N= { \left ( \boldsymbol a^H(f_N) \boldsymbol T^{-1} \boldsymbol a (f_N) \right ) }
pN=(aH(fN)T−1a(fN))。另外,我们定义一个新的向量
u
′
∈
C
N
×
1
\boldsymbol u^{\prime} \in \mathbb C^{N \times 1}
u′∈CN×1
u
j
′
=
u
j
−
p
N
e
−
i
2
π
(
j
−
1
)
f
N
u^{\prime}_j = u_j - p_N e^{-i 2 \pi (j-1) f_N}
uj′=uj−pNe−i2π(j−1)fN
可以被证明:
T
(
u
′
)
=
T
(
u
)
−
p
N
a
(
f
N
)
a
H
(
f
N
)
T
(
u
′
)
≽
0
rank
(
T
(
u
′
)
)
=
N
−
1
\begin{aligned} \boldsymbol T(\boldsymbol u^{\prime}) &= \boldsymbol T(\boldsymbol u) - p_N \boldsymbol a (f_N) \boldsymbol a^H(f_N) \\ \boldsymbol T(\boldsymbol u^{\prime}) & \succcurlyeq \boldsymbol 0 \\ \text{rank} \left ( \boldsymbol T(\boldsymbol u^{\prime}) \right ) &= N-1 \end{aligned}
T(u′)T(u′)rank(T(u′))=T(u)−pNa(fN)aH(fN)≽0=N−1
因此, T ( u ′ ) \boldsymbol T(\boldsymbol u^{\prime}) T(u′)满足第一种 r ≤ N − 1 r \leq N-1 r≤N−1的情况。因此,当 r = N r=N r=N时,分解并不唯一。
最后我们来证明
r
≤
N
−
1
r \leq N-1
r≤N−1时分解的唯一性,如果假设存在另一种分解形式:
T
=
A
(
f
′
)
P
′
A
H
(
f
′
)
,
p
j
′
>
0
\boldsymbol T = \boldsymbol A(f^{\prime}) \boldsymbol P^{\prime} \boldsymbol A^H(f^{\prime}), \ p^{\prime}_j > 0
T=A(f′)P′AH(f′), pj′>0,且
f
j
′
∈
T
f_j^{\prime} \in \mathbb T
fj′∈T各不相同,这时,我们有
A
(
f
′
)
P
′
A
H
(
f
′
)
=
A
(
f
)
P
A
H
(
f
)
\boldsymbol A(f^{\prime}) \boldsymbol P^{\prime} \boldsymbol A^H(f^{\prime}) = \boldsymbol A( \boldsymbol f ) \boldsymbol P \boldsymbol A^H( \boldsymbol f )
A(f′)P′AH(f′)=A(f)PAH(f)
那么,存在一个酉阵
Q
′
∈
C
r
×
r
\boldsymbol Q^{\prime} \in \mathbb C^{r \times r}
Q′∈Cr×r 使得
A
(
f
′
)
P
′
1
2
=
A
(
f
)
P
1
2
Q
′
\boldsymbol A(f^{\prime}) \boldsymbol P^{\prime \frac{1}{2}}=\boldsymbol A( \boldsymbol f ) \boldsymbol P^{\frac{1}{2}} \boldsymbol Q^{\prime}
A(f′)P′21=A(f)P21Q′,因此
A
(
f
′
)
=
A
(
f
)
P
1
2
Q
′
P
′
−
1
2
\boldsymbol A(f^{\prime}) = \boldsymbol A( \boldsymbol f ) \boldsymbol P^{\frac{1}{2}} \boldsymbol Q^{\prime} \boldsymbol P^{\prime -\frac{1}{2}}
A(f′)=A(f)P21Q′P′−21
上式意味着,对于 ∀ j ∈ { 1 , 2 , ⋯ , r } \forall j \in \{1,2,\cdots, r\} ∀j∈{1,2,⋯,r}, a ( f j ′ ) ∈ span { a ( f 1 ) , ⋯ , a ( f r ) } \boldsymbol a(f^{\prime}_j) \in \text{span} \left \{ \boldsymbol a(f_1), \cdots, \boldsymbol a(f_r) \right \} a(fj′)∈span{a(f1),⋯,a(fr)}。又因为在 r ≤ N − 1 r \leq N-1 r≤N−1时,任意两个分量 a ( f i ) \boldsymbol a(f_i) a(fi)与 a ( f j ) , i ≠ j \boldsymbol a(f_j), i\neq j a(fj),i=j都是线性独立的,因此必然有, { f j ′ } j = 1 r \{f^{\prime}_j\}_{j=1}^r {fj′}j=1r与 { f j } j = 1 r \{f^{}_j\}_{j=1}^r {fj}j=1r相等。由此可以得出,当 r ≤ N − 1 r \leq N-1 r≤N−1时,分解具有唯一性。
总结:
- 当 r ≤ N − 1 r \leq N-1 r≤N−1时,半正定Toeplitz矩阵的范德蒙德分解是唯一地;
- 当 r = N r = N r=N时,半正定Toeplitz矩阵的范德蒙德分解不唯一。
推论:任意PSD Toeplitz矩阵 T ( u ) ∈ C N × N \boldsymbol T(\boldsymbol u) \in \mathbb C^{ N \times N} T(u)∈CN×N可以被唯一地分解为:
T = ∑ k = 1 r p k a ( f k ) a H ( f k ) + σ I = A ( f ) d i a g ( p ) A H ( f ) + σ I \boldsymbol T = \sum_{k=1}^r p_k \boldsymbol a(f_k) \boldsymbol a^H(f_k) + \sigma \boldsymbol I = \boldsymbol A( \boldsymbol f ) diag(\boldsymbol p) \boldsymbol A^H( \boldsymbol f ) + \sigma \boldsymbol I T=k=1∑rpka(fk)aH(fk)+σI=A(f)diag(p)AH(f)+σI
其中 σ = λ m i n ( T ) \sigma = \lambda_{min}(\boldsymbol T) σ=λmin(T), r = rank ( T − σ I ) < N r = \text{rank}(\boldsymbol T - \sigma \boldsymbol I) < N r=rank(T−σI)<N, p k > 0 p_k >0 pk>0, f k ∈ T , k = 1 , ⋯ , r f_k \in \mathbb T, k=1,\cdots,r fk∈T,k=1,⋯,r are disjoint.
Remark: Note that the uniqueness of the decomposition above is guranteed by the condition that σ = λ m i n ( T ) \sigma=\lambda_{min}(\boldsymbol T) σ=λmin(T). If the condition is violated by letting 0 ≤ σ < λ m i n ( T ) 0 \leq \sigma < \lambda_{min}(\boldsymbol T) 0≤σ<λmin(T) (in such a case T \boldsymbol T T has full rank and r ≥ N r \geq N r≥N), then the deomposition cannot be unique.
参考
[1] Yang, Z., Li, J., Stoica, P., & Xie, L. (2016). Sparse Methods for Direction-of-Arrival Estimation. ArXiv, abs/1609.09596.




![[附源码]计算机毕业设计springboot水果管理系统](https://img-blog.csdnimg.cn/957ee6822f544b5a8080e53da451e971.png)