初见安——！！这里是咕咕咕好久好久的樱狸QvQ

考完初赛了 有一点点的空闲时间 来整理一下博客【因为发现忘性很大……超过一个月没用的东西就记不住了QAQ

前置知识：KMP，tire树。

一、AC自动机

其实AC自动机就是在tire树上KMP。

举个例子：给你一个串S，一个串T，求T在S中出现的次数。显然KMP线性匹配。

那么如果给你一个串S，很多串T，问你每个串在S中的出现次数呢？复杂度就不保了。这时就要用到AC自动机。

比如给的是abc，aab，abcba，acb，S串是abccbacbabcba。

我们对给的串建tire树：【图丑求放过

然后在这颗树上跟着走串S。

比如我们给这个图的点编号后，

s串abccbacbabcba会依次走过：1，4，5，然后发现下一个没有c了跳不动。

根据KMP的思想，我们在trie树上令fail指针表示与KMP类似的含义，也就是失配指针。fail[i]表示trie树上从根到当前点形成的字符串的后缀匹配前缀的最长串的结尾位置。那么上图的树中我们就可以建立fail指针：

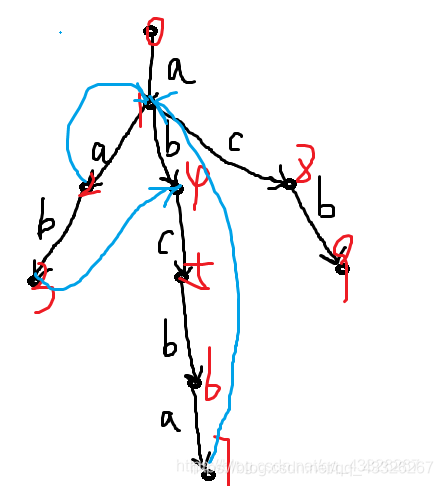
没有连边的都是指向根节点】

这样一来，当S失配后，就会沿着fail往回跳，缩小匹配的字符串。而S走的全过程中的子串都不重复，因为每走一步必然会相较于前一步多了第i个字符。所以每次形成的字符串的后缀都是答案之一。

接着上文的例子，S失配没法跳c后回到根节点0，然后继续跳b，失配；跳a，跳到1,8,9；然后回到0……

我们在trie树上记录每个点为末尾代表了哪些字符串，然后就可以统计答案了。

看一个例题吧：洛谷 【模板】AC自动机（简单版）

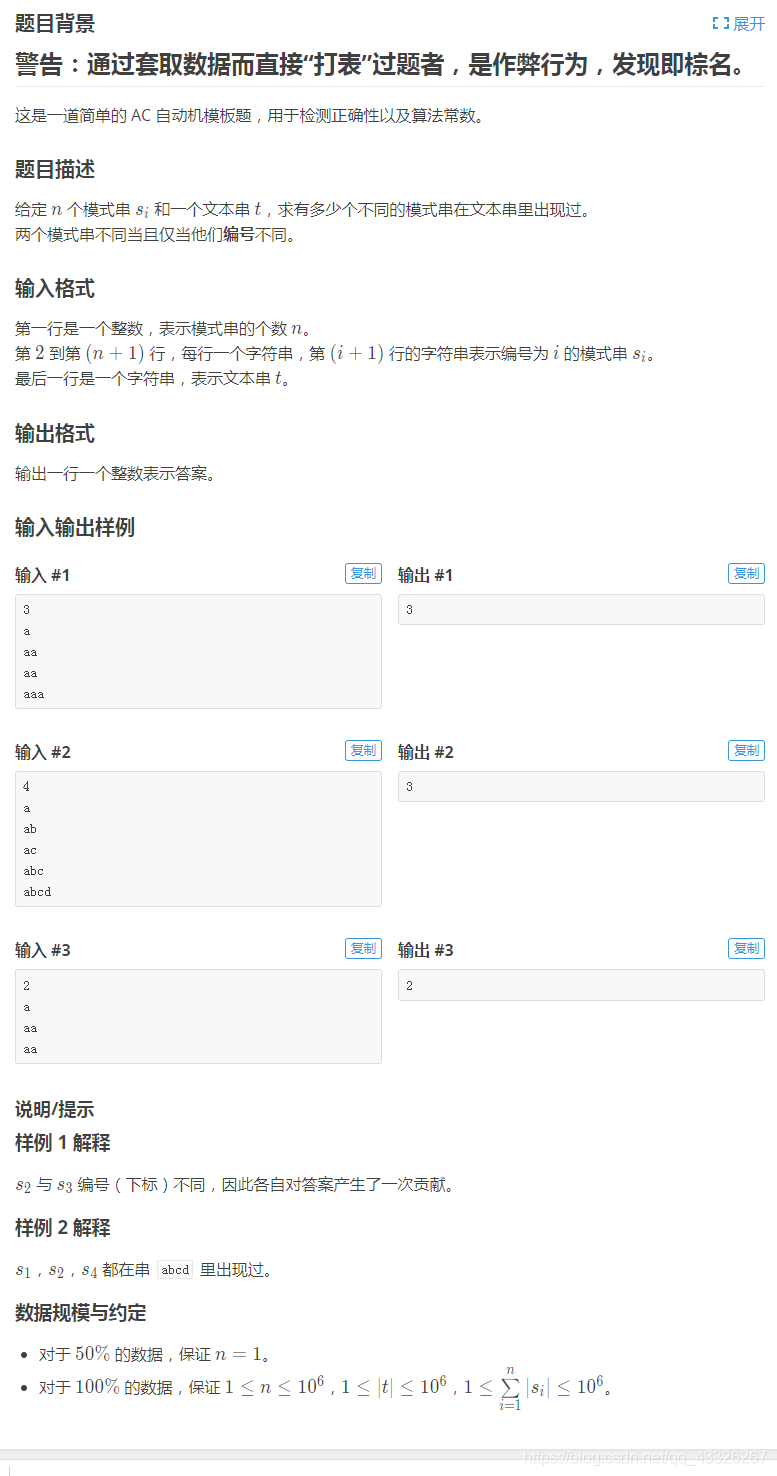
看看代码吧——

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#include<map>
#define maxn 1000006
using namespace std;
typedef long long ll;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int n, t[maxn][26], fail[maxn], num[maxn], tot = 0;
char s[maxn];
void add() {//建立trie树
	register int len = strlen(s), p = 0;
	for(int i = 0; i < len; i++) {
		int u = s[i] - 'a';
		if(!t[p][u]) t[p][u] = ++tot; p = t[p][u];
	}
	num[p]++;//表示以p结尾的字符串数
}

queue<int> q;
void build() {
	for(int i = 0; i < 26; i++) if(t[0][i]) q.push(t[0][i]);//bfs建立fail指针
	while(q.size()) {
		register int u = q.front(); q.pop();
		for(int i = 0, v; i < 26; i++) {
			v = t[u][i];
			if(v) fail[v] = t[fail[u]][i], q.push(v);//如果有儿子，就匹配过去
			else t[u][i] = t[fail[u]][i];//没有的话相当于路径压缩，直接连过去
		}
	}
}

int ans = 0;
void AC() {
	register int len = strlen(s), p = 0;
	for(int i = 0, u, v; i < len; i++) {
		u = s[i] - 'a';  p = t[p][u], v = p;
		while(v && num[v] != -1) {//暴力跳fail查询
			ans += num[v], num[v] = -1;
			v = fail[v];
		}
	}
}

signed main() {
	n = read();
	for(int i = 1; i <= n; i++) scanf("%s", s), add();
	build(); scanf("%s", s); AC();
	printf("%d\n" , ans);
	return 0;
}

（未完待续 咕太久了我也忘了后续要写啥QAQ