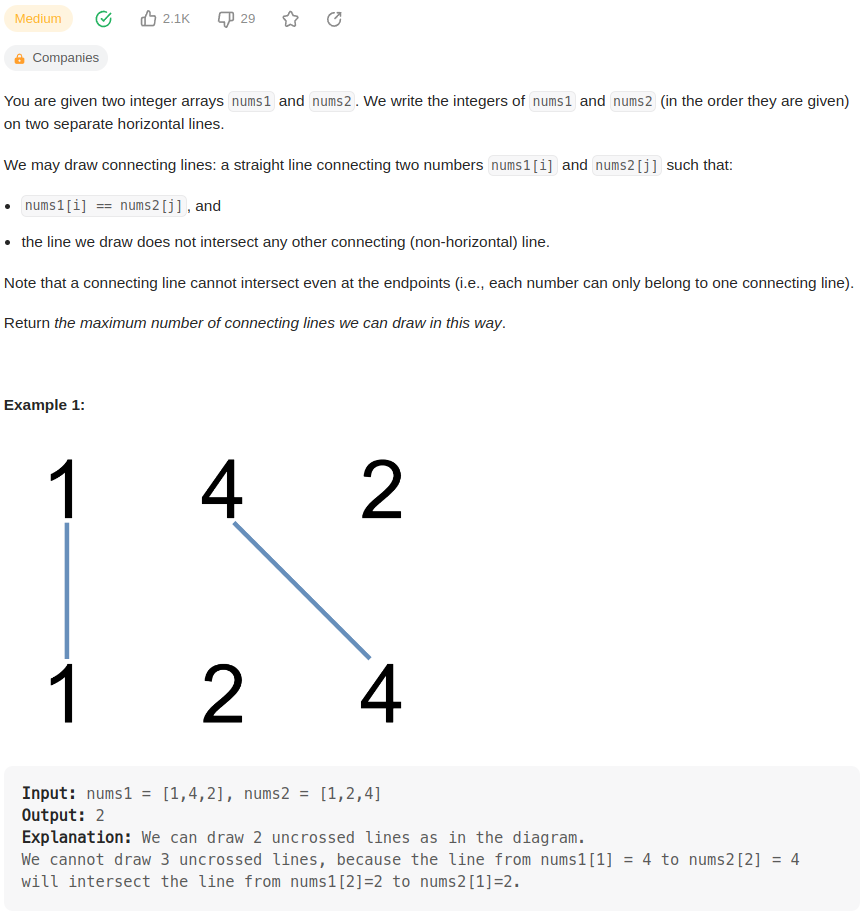
把数组nums1和nums2的元素排成2行，
从左到右把相同的元素连线，但是任意2条线不能交叉。
比如Example1中，可以连2个4，也可以连2个2，但是不能同时连，因为会交叉。
找出最多的连线数。

思路：

一开始会想从左到右遍历nums1中的数字，依次在nums2中找到对应的，
且只在nums2上一个数字的右边找下一个数字。
这么做是能找到其中一种情况的连线数，但是不一定能找到最大连线数。
比如：

1  2  3  4
2  3  4  1

第一次连1，直接连到了nums2的末尾，那下一次就无法再连线了。
而最大的连线数是3，也就是不连1，只连2，3，4.

所以需要找的是连于不连的选择间，最大的连线数。因此要用到DP，记录到每个位置 i 为止的最大连线数。
用二维DP，dp[ i ][ j ]表示nums1到i为止，nums2到 j 为止的最大连接数。
那么如果nums1[ i ] == nums2[ j ], 需要在dp[i-1][j-1]的连线数上增加一个，
即dp[ i ][ j ] = dp[i-1][j-1]+1.
如果nums1[i]和nums2[j]不相等，那么保留之前的连线数，需要取dp[i-1][j]和dp[i][j-1]较大的一个。

public int maxUncrossedLines(int[] nums1, int[] nums2) {
    int n1 = nums1.length;
    int n2 = nums2.length;
    int[][] dp = new int[n1+1][n2+1];

    for(int i = 1; i <= n1; i++) {
        for(int j = 1; j <= n2; j++) {
            if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1]+1;
            else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
        }
    }
    return dp[n1][n2];
}