一.概念
边:一棵n个结点树有n-1条边
结点深度:从根到当前结点的路径的深度。
结点高度:从当前结点到叶子结点最长路径的长度。
树的性质
- 树中的结点总数等于所有结点的度+1;
- m叉树中第i(i>=1)层上至多可以有m^(i-1)个节点;

- 高度为h(h>=1)的m叉树至多有(m^h -1)/(m-1)
- 具有n个结点的m叉树的最小高度为[logm(n(m-1)+1)]。取上限,向上取整。
![]()
二叉树
二叉树每个结点只能有两棵子树,分别被称为左子树和右子树。
满二叉树:一棵高度为h,且含有2^h-1个结点的二叉树被称之为满二叉树
对于编号为i的结点,左子节点的编号为2i,右子节点的编号为2i+1,双亲结点的编号为[i/2](向下取整)
完全二叉树:一颗高度为h,有n个结点的完全二叉树,它的每个结点都与高度相同的满二叉树中的结点编号一一对应。
二叉排序树:(二叉查找树)树上任意结点如果存在左子树和右子树,则左子树上所有结点元素的值都小于该结点,右子树上所有结点元素的值都大于该结点。
二叉树的性质:
- 一棵非空的二叉树,n表示结点总数,n0表示度为0的结点树,n1表示度为1的结点树,n2表示度为2 的节点数
n=n0+n1+n2
n=n1+2n2+1
n0=n2+1 - 一棵非空的二叉树的第k层最多只能有2^(k-1)个结点
- 高度为h的二叉树最多只能有2^h-1个结点
二.完全二叉树的存储
完全二叉树的顺序存储

普通二叉树的顺序存储,添加空结点,补全成为完全二叉树,数组中用0或者其他特殊值填充。可能造成浪费。

二叉树的遍历
层次遍历:利用队列先进先出的性质
// 二叉树层次遍历。
void LevelOrder(BiTree TT)
{
SeqQueue QQ; // 创建循环队列。
InitQueue(&QQ); // 初始化循环队列。
ElemType ee = TT; // 队列的元素是二叉树。
InQueue(&QQ, &ee); // 把根结点当成队列的元素入队。
while (IsEmpty(&QQ) != 1) // 队列不为空。
{
OutQueue(&QQ, &ee); // 队头元素出队。
visit(ee); // 访问出队元素。
if (ee->lchild != NULL) InQueue(&QQ, &ee->lchild); // 如果出队元素有左结点,左结点入队。
if (ee->rchild != NULL) InQueue(&QQ, &ee->rchild); // 如果出队元素有右结点,右结点入队。
}
}先序遍历:根左右
中序遍历:左根右
后序遍历:左右根
最深的子树开始向上遍历
二叉树的实现
递归实现
// 二叉树的先序遍历。
void PreOrder(BiTree TT)
{
if (TT == NULL) return;
visit(TT); // 访问子树TT的根结点。
PreOrder(TT->lchild); // 遍历左子树。
PreOrder(TT->rchild); // 遍历右子树。
}非递归实现:利用栈的性质
前序遍历:

由遍历序列构造二叉树
由一种遍历序列不能还原出来唯一的二叉树。

线索二叉树:
在含有n个结点的二叉链表中,有n+1个空指针,能否利用这些空指针来存放前驱和后继结点的地址?然后像遍历链表一样方便的遍历二叉树的序列?
线索二叉树可以部分解决上述问题,加快了在序列中查找前驱和后继结点的速度,但增加了在树中插入和删除结点的难度。

typedef struct TBTNode
{
char data; // 存放结点的数据元素。
struct TBTNode* lchild; // 指向左子结点地址的指针。
struct TBTNode* rchild; // 指向右子结点地址的指针。
unsigned char ltag, rtag; // 左右指针的类型,0-非线索指针,1-线索指针。
}TBTNode, * TBTTree;先序线索树求后继

后续线索树求前驱?????
二叉排序树

二叉排序树(二叉搜索树,二叉查找树BST)一棵非空的二叉排序树具有如下性质:
- 1.如果左子树不空,则左子树上所有结点的值都小于根节点的值
- 2.如果右子树不为空,右子树上所有节点的值都大于根节点的值
- 3.左右子树也分别是二叉排序树
中序排列的结果:结点时升序
创建二叉排序树
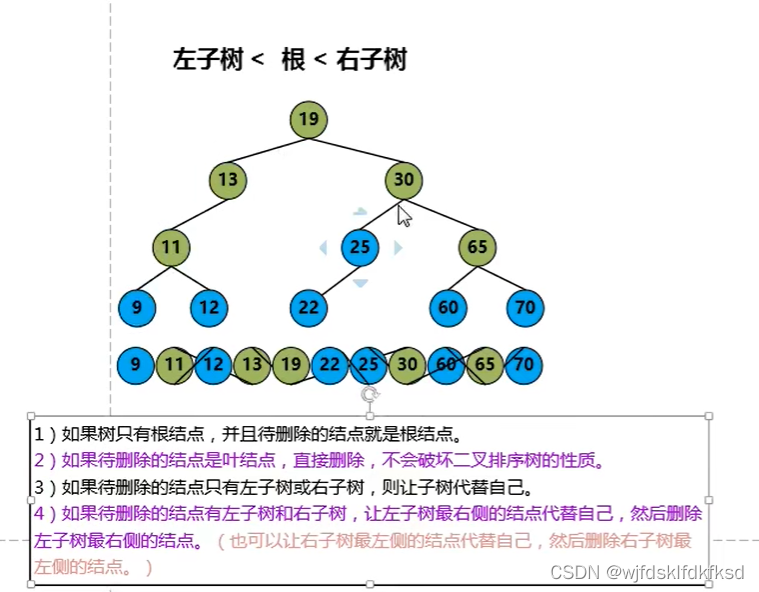
左子树<根<右子树
1.相同的序列创建的二叉排序树是唯一的
2.同一集合创建的二叉排序树是不同的
3.用二叉树的先序遍历序列创建的二叉排序树与原数相同
删除二叉树的结点
ASL (average Search Length)平均查找长度:

平衡二叉树:任意结点的左右高度不超过1.

平衡因子为左子树高减去右子树高
AVL树规定每个结点的平衡因子的绝对值不大于1
LL型状态:右旋



LR双旋:先左转B结点,再右旋A结点

节点的度:子树的个数
树的度:所有节点度中的最大值
叶子节点:度为0的节点
非叶子节点:度不为0的节点
层数:根节点在第一层
节点的深度:从根节点到当前节点的唯一路径上的节点总数
节点的高度:从当前节点到最远叶子节点的路径上的节点总数
有序树:树中任意节点的子节点之间有顺序关系
二叉树的特点:
- 每个节点的度最大为2
- 左子树和右子树是有顺序的
二叉树是有序树还是无序树?有序树
非空二叉树的性质:



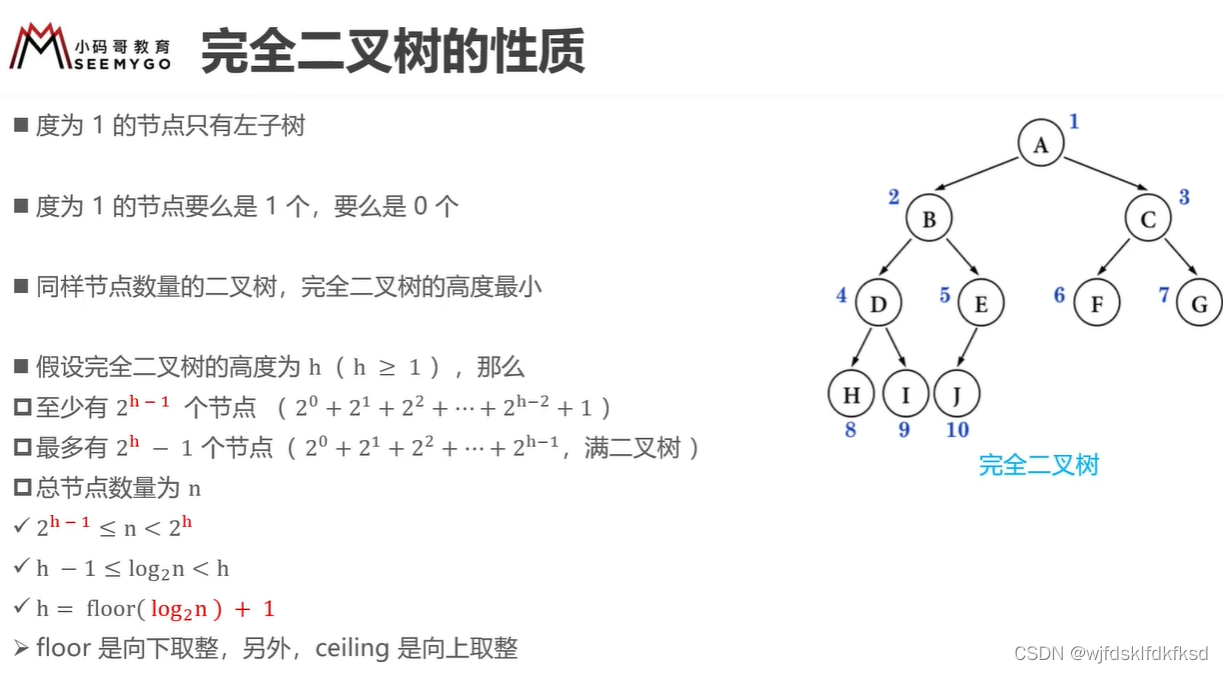

n0=floor((n+1)/2);




层序遍历:利用队列的性质
层序遍历
1.将根节点入队
2.循环执行以下操作,直到队列为空
a.将队头节点A出队,访问
b.将A的左子节点入队
c.将A的右子节点入队
求二叉树的高度:
法一:利用递归
int heightByRecursion(Node<T>* node)
{
if (node == nullptr) return 0;
return 1 + std::max(height(node->m_left), height(node->m_right));
}法二:迭代版本 每一层访问完后,下一层的长度就是队列的长度
int heightByIterator(Node<T>* node)
{
if (node == nullptr) return 0;
int iHeight = 0;
int iLaySize = 1;// 每一层的元素数量 初始化第一层的长度为1
//先将头节点入队
std::queue<T> q;
q.push(node);
//循环操作,直到队列为空
while (!q.empty()) {
Node<T>* head = q.front();
std::cout << head->element;
q.pop();
iLaySize--;
if (head->m_left != nullptr)
q.push(head->m_left);
if (head->m_right != nullptr)
q.push(head->m_right);
if (0 == iLaySize)//意味着即将要访问下一层
{
iLaySize = q.size();
iHeight++;
}
}
return iHeight;
}如何判断一棵树是否为完全二叉树

bool isCompleteBT()
{
std::queue<Node<T>*> q;
q.push(m_root);
bool bLeaf = false;
while (!q.empty()) {
Node<T>* head = q.front();
q.pop();
if (bLeaf && head->isLeaf())
{
return false;
}
/*************************/
if (head->m_left != nullptr && head->m_right != nullptr)
{
q.push(head->m_left);
q.push(head->m_right);
}
else if (head->m_left == nullptr && head->m_right != nullptr)
{
return false;
}
else if
(
(head->m_left != nullptr && head->m_right == nullptr) ||
(head->m_left == nullptr && head->m_right == nullptr)
)//后面遍历的节点必须是叶子节点
{
if(head->m_left != nullptr) q.push(head->m_left);
bLeaf = true;
}
/*************************/
}
return true;
}反转二叉树(所有左右子节点交换)
//利用前序遍历访问每一个节点 递归方式 中序方式有问题
Node<T>* inverTree(Node<T>* root)
{
if (root == nullptr) return root;
Node<T>* node = root->m_left;
root->m_left = root->m_right;
root->m_right = node;
inverTree(root->m_left);
inverTree(root->m_right);
}
//利用中序遍历访问每一个节点 递归方式
Node<T>* inverTreePreOrder(Node<T>* root)
{
if (root == nullptr) return root;
inverTree(root->m_left);
Node<T>* node = root->m_left;
root->m_left = root->m_right;
root->m_right = node;
inverTree(root->m_left);//这里仍然要传左子节点,因为左右已经交换
}
//利用迭代方式 层序遍历 反转二叉树
bool inverTreeLayOrder(Node<T>* root)
{
Node<T>* head = root;
std::queue<T> q;
q.emplace(head);
while (!q.empty())
{
head = q.front();
q.pop();
Node<T>* tempNode = head->m_left;
head->m_left = head->m_right;
head->m_right = tempNode;
if (head->m_left != nullptr)
q.emplace(head->m_left);
if (head->m_right != nullptr)
q.emplace(head->m_right);
}
}根据遍历结果复原唯一的一棵二叉树
1.前序遍历+中序遍历
2.后序遍历+中序遍历
前序遍历+后序遍历,如果它是一棵真二叉树,结果是唯一的。不然,结果不唯一。
原因:如果左右子树有一个为空,通过前序遍历和后序遍历不能确定是左子树为空还是右子树为空。如果是一棵真二叉树,则左右子树要么都存在,要么为空。
前驱节点
前驱节点指 中序遍历时的前一个结点
对于二叉排序树,前驱结点是该结点的左子树的最大结点。

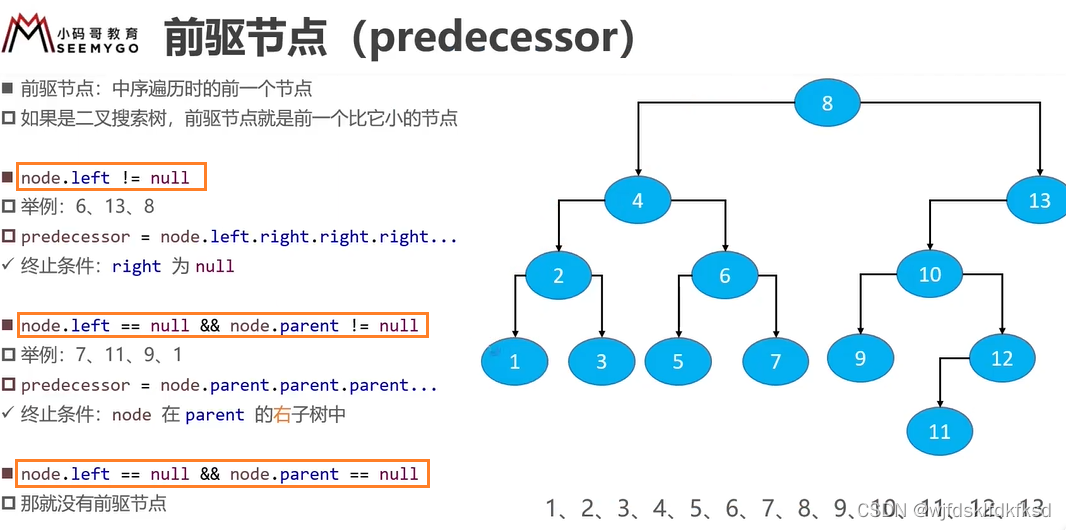
/*查找前驱结点*/
Node<T>* preDecessor(Node<T>* node)
{
if (node == nullptr) return nullptr;
Node<T>* tempNode = nullptr;
if (node->m_left != nullptr)
{
Node<T>* p = node->m_left;
while (p != nullptr)
{
p = p->m_right;
}
return p;
}
//从父节点 祖父结点中寻找前驱结点
while(node->m_parent != nullptr && node == node->m_parent->m_left)
//父节点不为空并且该节点是父节点的左子树
{
node = node->m_parent;
}
//
return node->m_parent;
}后继结点:中序遍历时的后一个结点,如果是二叉搜索树,后继结点就是后一个比它大的结点
删除结点
a.如果是叶子结点,直接删除
b.度为1的结点,用子结点替代原结点的位置。
1.如果node是左子结点
child.parent = node.parent;
node->parent->left = child;
2.如果node是右子结点
child.parent = node.parent;
node->parent->right = child;
3.如果node是root
root = child;child.parent=nullptr;
c.度为2的结点
找前驱或者后继结点覆盖该节点,删除前驱或者后继结点。
注意:如果一个结点的度为2,那么它的前驱,后继节点的度只能是1和0。