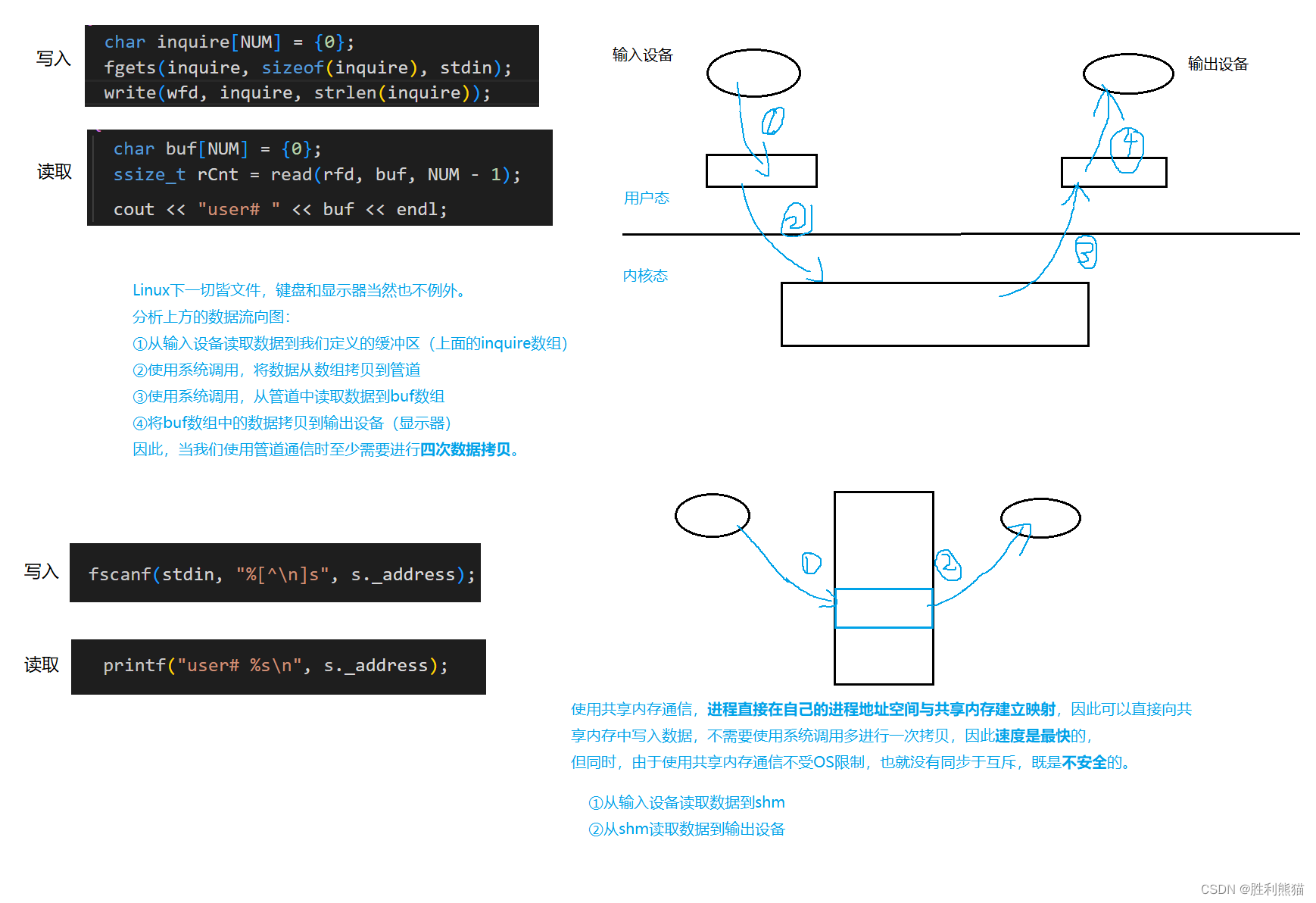
1 K-means方案

K-means 算法是一种自动将相似数据点聚集在一起的方法。

• 具体来说，你得到了一个训练集{,...,}，并且您希望将数据分组为几个有凝聚力的“集群”。

• K-means 是一个迭代过程

  • 首先猜测初始质心，
  • 然后改进这个猜测
    • 反复将样本分配到它们最近的质心，
    • 然后根据分配重新计算质心。

• 在伪代码中，K-means算法如下：

• # Initialize centroids
  # K is the number of clusters
  centroids = kMeans_init_centroids(X, K)
  
  for iter in range(iterations):
      # Cluster assignment step: 
      # Assign each data point to the closest centroid. 
      # idx[i] corresponds to the index of the centroid 
      # assigned to example i
      idx = find_closest_centroids(X, centroids)
  
      # Move centroid step: 
      # Compute means based on centroid assignments
      centroids = compute_means(X, idx, K)

• 算法的内循环重复执行两个步骤：

  • (i) 分配每个训练示例到它最近的质心，和
  • (ii) 使用分配给它的点重新计算每个质心的平均值。

• 这𝐾钾-均值算法将始终收敛到质心的一些最终均值集。

• 然而，收敛的解决方案可能并不总是理想的，并且取决于质心的初始设置。

  • 因此，在实践中，K-means 算法通常使用不同的随机初始化运行几次。
  • 在不同随机初始化的这些不同解决方案之间进行选择的一种方法是选择具有最低成本函数值（失真）的解决方案。

您将在接下来的部分中分别实现 K-means 算法的两个阶段。

• 您将从完成开始find_closest_centroid，然后继续完成compute_centroids。

1.1 寻找最近的质心

数据格式：X为矩阵

First five elements of X are:
 [[1.84207953 4.6075716 ]
 [5.65858312 4.79996405]
 [6.35257892 3.2908545 ]
 [2.90401653 4.61220411]
 [3.23197916 4.93989405]]
The shape of X is: (300, 2)

 质心列表为：

 initial_centroids = np.array([[3,3], [6,2], [8,5]])

任务是完成find_closest_centroids.

• 此函数采用数据矩阵X和内部所有质心的位置centroids
• 它应该输出一个一维数组idx（其元素数与X相同），其中包含最近质心的索引{ 1 , . . . , 𝐾}， 𝐾是每个训练样本的质心总数。
• 具体来说，对于每个例子我们设置
  
  其中，
• 是最接近的质心的索引𝑥( 𝑖 )（对应于idx[i]起始代码），
• 是的位置（值）𝑗th 质心。（存储centroids在起始代码中）

 代码：

def find_closest_centroids(X, centroids):
    """
    Computes the centroid memberships for every example
    
    Args:
        X (ndarray): (m, n) Input values      
        centroids (ndarray): k centroids
    
    Returns:
        idx (array_like): (m,) closest centroids
    
    """

    # Set K
    K = centroids.shape[0]

    # You need to return the following variables correctly
    idx = np.zeros(X.shape[0], dtype=int)

    for i in range(X.shape[0]):
        distance = [] 
        for j in range(centroids.shape[0]):
            norm_ij = np.linalg.norm(X[i] - centroids[j]) #numpy计算几何距离
            distance.append(norm_ij)
        
        idx[i] = np.argmin(distance)
    
    return idx

 1.2 计算质心均值

给定每个点到质心的分配，算法的第二阶段为每个质心重新计算分配给它的点的平均值。

完成compute_centroids以下内容以重新计算每个质心的值

• 具体来说，对于每个质心我们设置

  

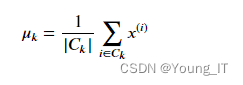
  其中，

  • 是分配给质心的示例集𝑘
  • 是集合中的示例数

   具体来说，如果两个例子说和被分配到质心𝑘=2, 那么你应该更新质心：

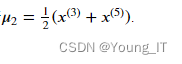
   代码：

def compute_centroids(X, idx, K):
    """
    Returns the new centroids by computing the means of the 
    data points assigned to each centroid.
    
    Args:
        X (ndarray):   (m, n) Data points
        idx (ndarray): (m,) Array containing index of closest centroid for each 
                       example in X. Concretely, idx[i] contains the index of 
                       the centroid closest to example i
        K (int):       number of centroids
    
    Returns:
        centroids (ndarray): (K, n) New centroids computed
    """
    
    # Useful variables
    m, n = X.shape
    
    # You need to return the following variables correctly
    centroids = np.zeros((K, n))
    
    for k in range(K):   
        points = X[idx == k]
        centroids[k] = np.mean(points, axis = 0)
    
    return centroids