多处最优服务次序问题——算法设计与分析（C实现）

news2024/11/28 11:34:44

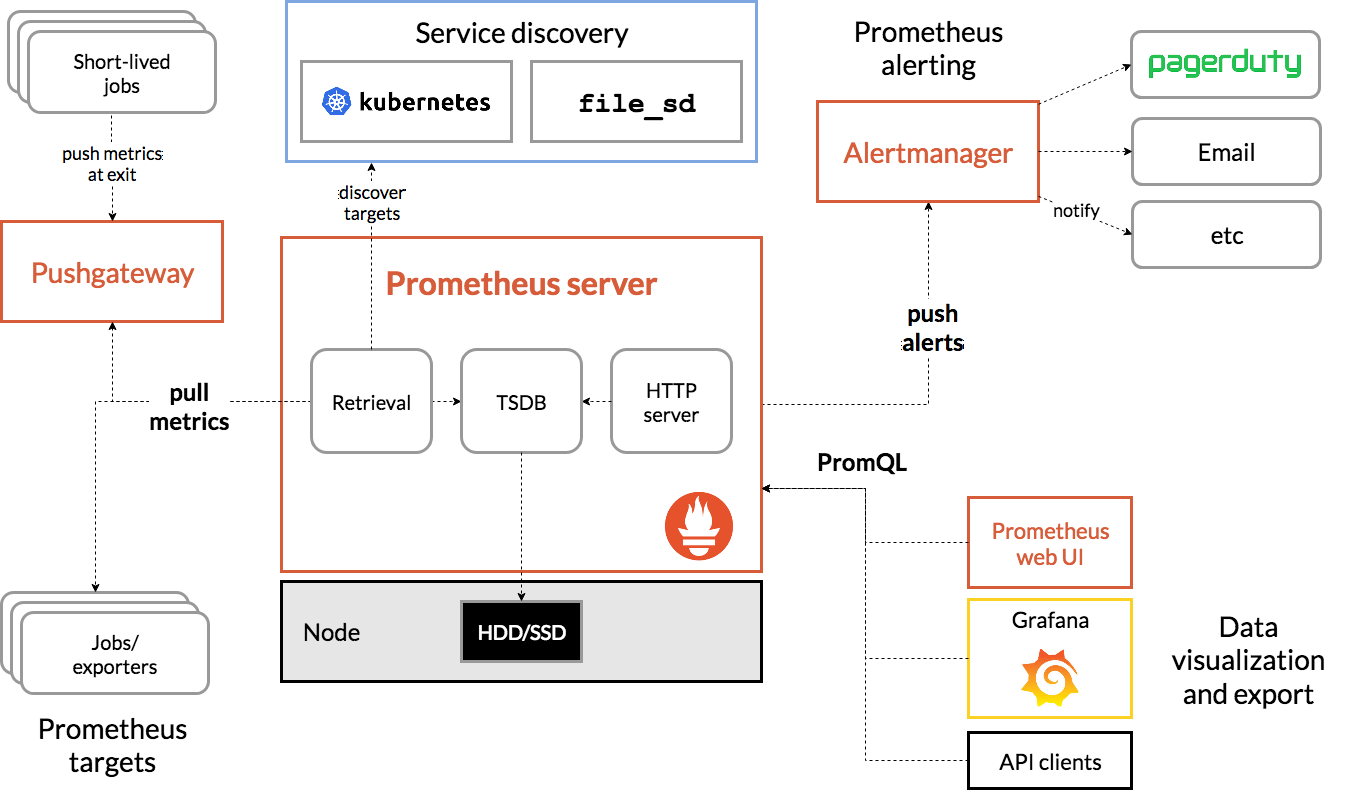
问题描述：设有n个顾客同时等待一项服务。顾客i需要的服务时间为 $t_{i}(1\leq i\leq n)$ ，共有s处可以提供此项服务。应该如何安排n个顾客的服务次序，才能使平均等待时间达到最小？平均等待时间是n个顾客的等待服务时间的总和除以n。

算法设计：对于给定的n个顾客需要的服务时间和s的值，计算最优服务次序。

数据输入：由文件input.txt给出输入数据。第1行有2个正整数n和s，表示有n个顾客且有s处可以提供服顾客需要的服务。接下来的1行中有n个正整数，表示n个顾客需要的服务时间。

结果输出：将计算的最小平均等到时间输出到文件output.txt。

基本思想：

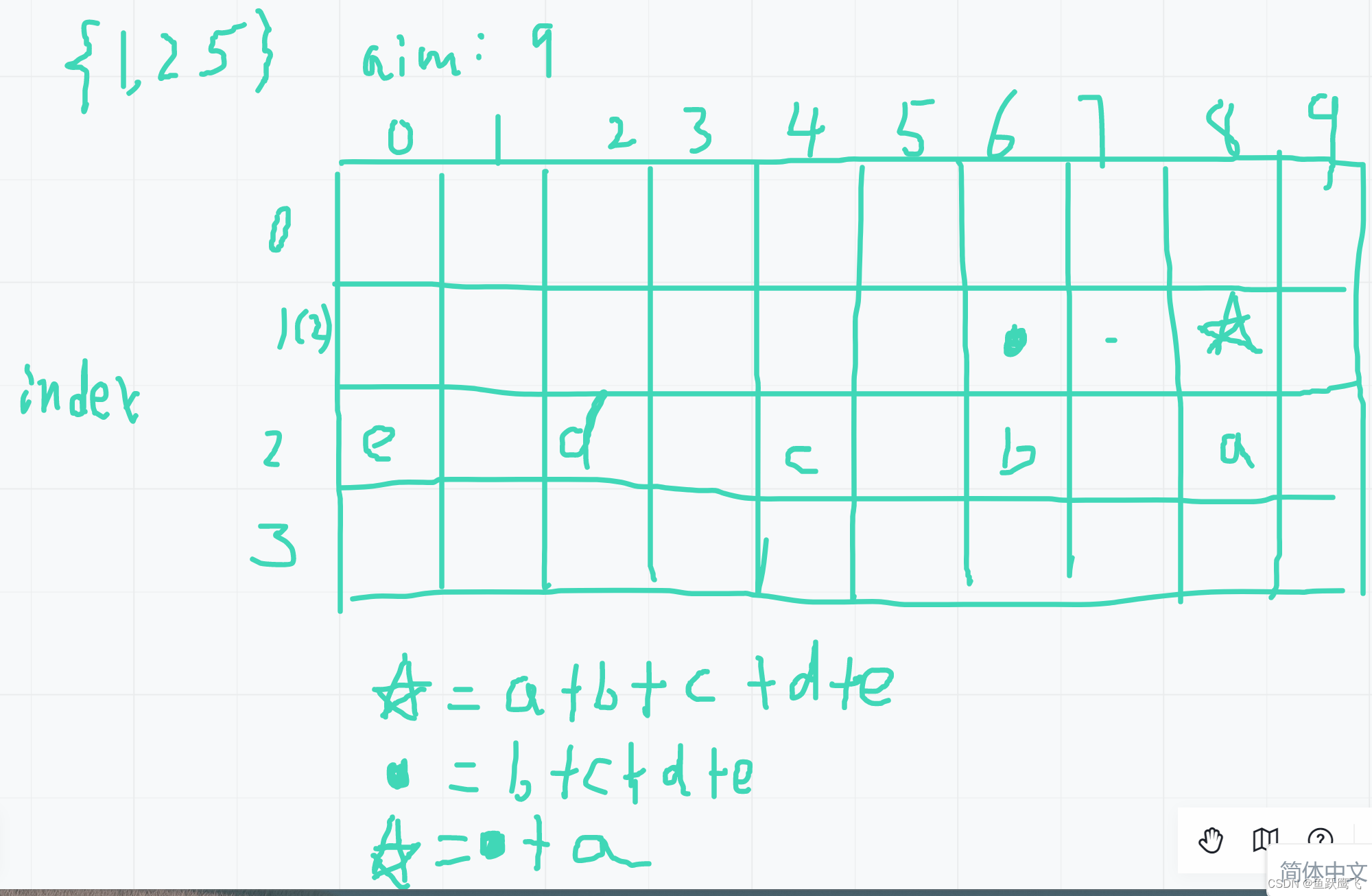
该题是贪心算法的典型，只需要将所有的任务按照截至时间递增进行排序，然后将任务逐个分配给每一个服务器。即将等待的人逐个分配到每一个服务处。
重在于统计每一个任务等待时间，然后计算平均等待时间。
需要注意的是，这里的等待时间是相对于完成任务的时间点，等待时间包括完成任务所花费的时间和等待分配到的时间，即等待时间=执行时间+执行前等待分配的时间

具体代码实现如下：

#include<stdio.h>

//选出当前等待时间最小的服务处 
int SelectMin(int* wait,int s)
{
    int min = wait[0];
    int index = 0;
    for (int i = 0; i < s; i++) 
	{
        if (min > wait[i]) 
		{
            min = wait[i];
            index = i;
        }
    }
    return index;
}

//安排顾客，计算平均等待时间 
int Greedy(int* wait, int *arr, int n,int s) 
{
    int sum = 0;
    int index;
    for (int i = 0; i < n; i++) 
	{
        index = SelectMin(wait, s);
        wait[index] += arr[i];
        sum += wait[index];
    }
    return sum / n;	
}

//对顾客的执行时间进行从小到大的排序 
void sort(int* arr,int n)
{
	int temp;
	 for(int i=0;i<n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(arr[j]>arr[j+1])
                {
                    temp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=temp;
                    }
             }
        }
}


int main()
{
    int n,s,res;
    
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    
    scanf("%d %d",&n,&s);//从文件中取出顾客人数和服务处数量 
    
    int wait[s];
    int arr[n];
    
    for(int i=0;i<n;i++)
    {
    	scanf("%d",&arr[i]);
	}
    
    sort(arr, n);		
    res= Greedy(wait, arr, n, s);

     printf("%d",res);
    return 0;
}

现在让我们来检验一下代码的正确性：

（1）首先在程序所在路径下建立两个题目所需要的文本文件：input.txt output.txt