如果在动态规划的过程中没有枚举行为,那严格位置依赖和傻缓存的方式并没有太大区别,但是当有枚举行为的时候(一个位置依赖于多个位置),那严格位置依赖是有优化空间的,枚举行为也许可以省去,题目:
| arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。 每个值都认为是一种面值,且认为张数是无限的。 返回组成aim的方法数 例如:arr = {1,2},aim = 4 方法如下:1+1+1+1、1+1+2、2+2 一共就3种方法,所以返回3 |
这个题目的动态规划普遍位置({1,8})的依赖,我们原来dp[1][8] = dp [2][8] + dp[2][6] + dp[2][4] + dp[2][2] + dp[2][0]
而dp[1][6] = dp[2][6] + dp[2][4] + dp[2][2] + dp[2][0]
我们可以看到计算dp[2][8]时候用到的 dp[2][6] + dp[2][4] + dp[2][2] + dp[2][0]之前其实是计算过的,这个值就是dp[1][6]
所以可以简化为dp[1][6] + dp[2][8]
普遍位置就是dp[index][rest] = dp[index+1][rest] + dp[index][rest-arr[index]]
dp[index][rest-arr[index]]这个要先判断存在不存在
也就是它依赖于它的下方和左边,dp数组按照从下到上,从左到右的顺序初始化即可
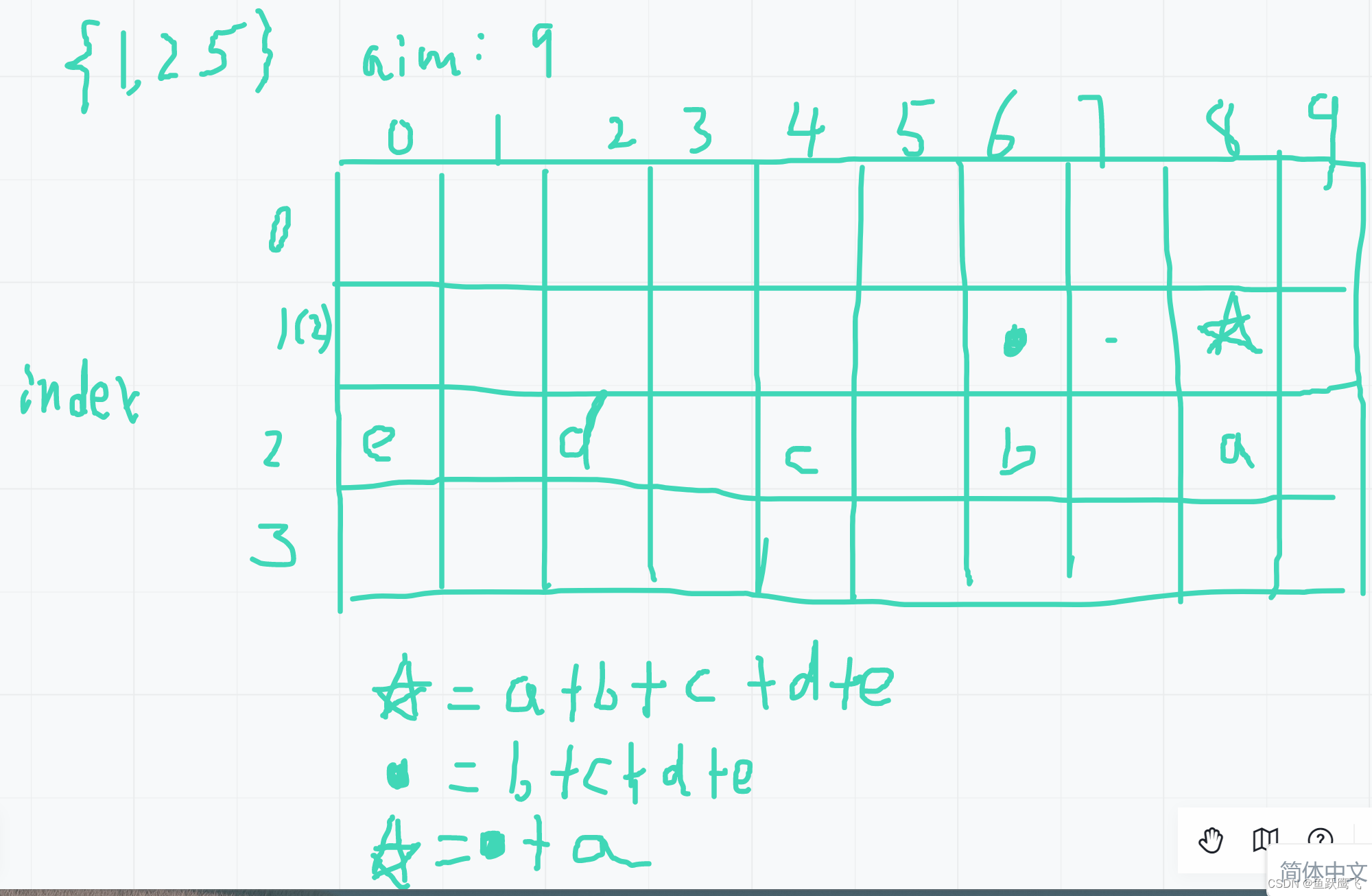
对应的代码如下:
package dataStructure.recurrence.practice;
/**
* arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。
* 每个值都认为是一种面值,且认为张数是无限的。
* 返回组成aim的方法数
* 例如:arr = {1,2},aim = 4
* 方法如下:1+1+1+1、1+1+2、2+2
* 一共就3种方法,所以返回3
*/
public class CoinsWayNoLimit {
public static int coinsWay(int[] arr, int aim) {
return process1(arr, 0, aim);
}
/**
* 动态规划的解法-原始版
* 根据递归,可变的参数是index和rest,变化范围分别是0~arr.length, 0~rest
* @param arr 原始的数组
* @param aim 要组成的目标
* @return
*/
public static int coinsWayDp(int[] arr, int aim) {
int[][] dp = new int[arr.length + 1][aim + 1];
//最后一行只有0位置是1,其他都是0(0是int默认值,不需要初始化)
dp[arr.length][0] = 1;
//根据递归,所有的(index, rest)都依赖于下一行前面的某个位置
//所以行必须从下往上,列初始化的顺序无所谓
for(int index = arr.length - 1; index >=0; index --) {
for(int rest = 0; rest <= aim; rest ++) {
int ways = 0;
for(int num = 0; num * arr[index] <= rest; num ++) {
ways += dp[index + 1][rest - (num * arr[index])];
}
dp[index][rest] = ways;
}
}
return dp[0][aim];
}
/**
* 动态规划的解法-原始版
* 根据递归,可变的参数是index和rest,变化范围分别是0~arr.length, 0~rest
* @param arr 原始的数组
* @param aim 要组成的目标
* @return
*/
public static int coinsWayDpBest(int[] arr, int aim) {
int[][] dp = new int[arr.length + 1][aim + 1];
//最后一行只有aim位置是1,其他都是0(0是int默认值,不需要初始化)
dp[arr.length][0] = 1;
//根据递归,所有的(index, rest)都依赖于下一行前面的某个位置
//所以行必须从下往上,这里我们要省掉枚举行为,一个位置依赖于他下面的位置和他前面的某个位置,所以必须从前往后
for(int index = arr.length - 1; index >=0; index --) {
for(int rest = 0; rest <= aim; rest ++) {
//这是倒数第二行,他下面肯定有位置
dp[index][rest] = dp[index + 1][rest];
//但是左边的位置rest-arr[index]不一定存在,所以要做判断
if(rest-arr[index] >= 0) {
//如果存在就加上
dp[index][rest] += dp[index][rest-arr[index]];
}
}
}
return dp[0][aim];
}
/**
* 递归黑盒方法,从index号下标开始组成left
* @param arr 原始的面值数组,每个面值都是无限的
* @param index 当前要考虑的位置下标
* @param rest 还差多少钱
* @return
*/
public static int process1(int[] arr, int index, int rest) {
if(rest < 0) return 0;
if(index == arr.length) {
return rest == 0? 1 : 0;
}
int ways = 0;
for(int num = 0; num * arr[index] <= rest; num++) {
ways += process1(arr, index + 1, rest - (num * arr[index]));
}
return ways;
}
public static void main(String[] args) {
int[] arr = {1,2};
int aim = 4;
int ways = coinsWay(arr, aim);
System.out.println(ways);
int waysDp1 = coinsWayDp(arr, aim);
System.out.println(waysDp1);
int waysDpBest = coinsWayDpBest(arr, aim);
System.out.println(waysDpBest);
}
}
省去了枚举行为,结果完全一致,原来的时间复杂度是O(N * M * K),现在的话变成了O(N * M)
其中K是rest/数组中最小的那个面值
个人的总结是:如果某个位置只依赖它的90度角范围内的枚举都是可以优化的(上、左 上、左上、左 等等)
欢迎私信讨论