简单线性回归

第一步是为Stan模型编写文件。这包含一个文件linreg.stan：

视频：线性回归中的贝叶斯推断与R语言预测工人工资数据案例

贝叶斯推断线性回归与R语言预测工人工资数据

，时长09:58

R的Stan


data {
  int N;
  vector[N] x;
  vector[N] y;
}

model {
  y ~ normal(alpha + beta * x, sigma);
}

该文件的第一部分称为数据，它声明了将作为输入传递给Stan的标量，向量和矩阵。

接下来，我们可以通过运行以下R代码来模拟数据集，并使用Stan和我们的文件linreg.stan来拟合模型：

stan(file = 'linreg. ', data = mydata, iter = 1000,   = 4)

第一次安装Stan模型时，模型编译成C ++时会有几秒钟的延迟。然而，一旦编译了模型，就可以将其应用于新的数据集而无需重复编译过程（执行模拟研究具有很大的优势）。

在上面的代码中，我们要求Stan运行4个独立的链，每个链有1000次迭代。运行后，我们可以通过以下方式汇总输出：

Inference for Stan model: linreg.
4 chains, each with iter=1000; warmup=500; thin=1; 
post-warmup draws per chain=500, total post-warmup draws=2000.

        mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
alpha  -0.10    0.00 0.10  -0.29  -0.16  -0.10  -0.04   0.09  1346    1
beta    0.95    0.00 0.11   0.75   0.88   0.95   1.02   1.17  1467    1
sigma   0.98    0.00 0.07   0.85   0.93   0.98   1.03   1.12  1265    1
lp__  -47.54    0.06 1.24 -50.77 -48.02 -47.24 -46.68 -46.17   503    1

Samples were drawn using NUTS(diag_e) at Mon Jun 08 18:35:58 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

对于回归斜率β，我们的后验均值为0.95（接近用于模拟数据的真实值1）。为了形成95％的后验置信区间，我们简单地采用取样后验的2.5％和97.5％的百分位数，这里是0.75到1.17。

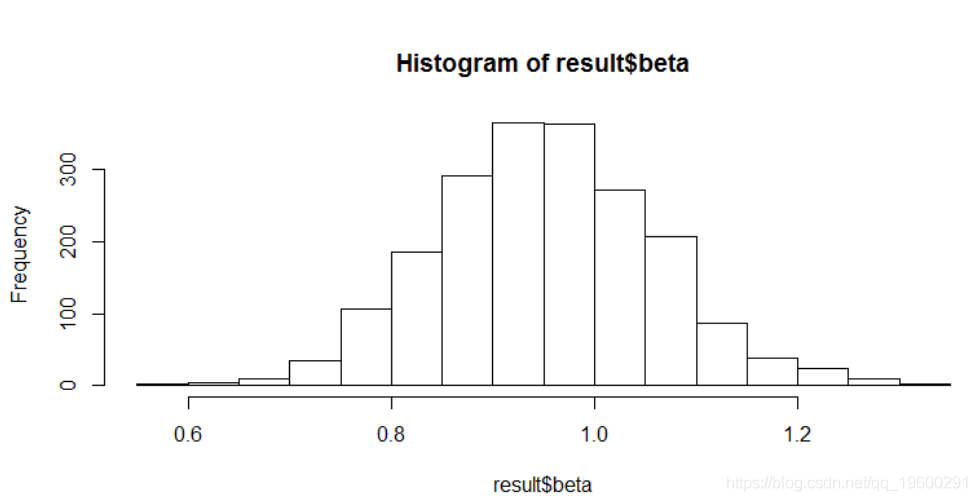
您可以从拟合的模型中获取各种其他数量。一种是绘制其中一个模型参数的后验分布。要获得回归斜率，我们可以执行以下操作：


hist(result$beta)

β后验分布直方图

现在让我们使用标准普通最小二乘拟合线性模型：

Residuals:
    Min      1Q  Median      3Q     Max 
-1.9073 -0.6835 -0.0875  0.5806  3.2904 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.10280    0.09755  -1.054    0.295    
x            0.94753    0.10688   8.865  3.5e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9707 on 98 degrees of freedom
Multiple R-squared:  0.4451,	Adjusted R-squared:  0.4394 
F-statistic:  78.6 on 1 and 98 DF,  p-value: 3.497e-14

这给出了我们对斜率0.95的估计，与Stan的后验平均值相差2位小数，标准误差为0.11，这与Stan的后验SD相同。