图的创建：

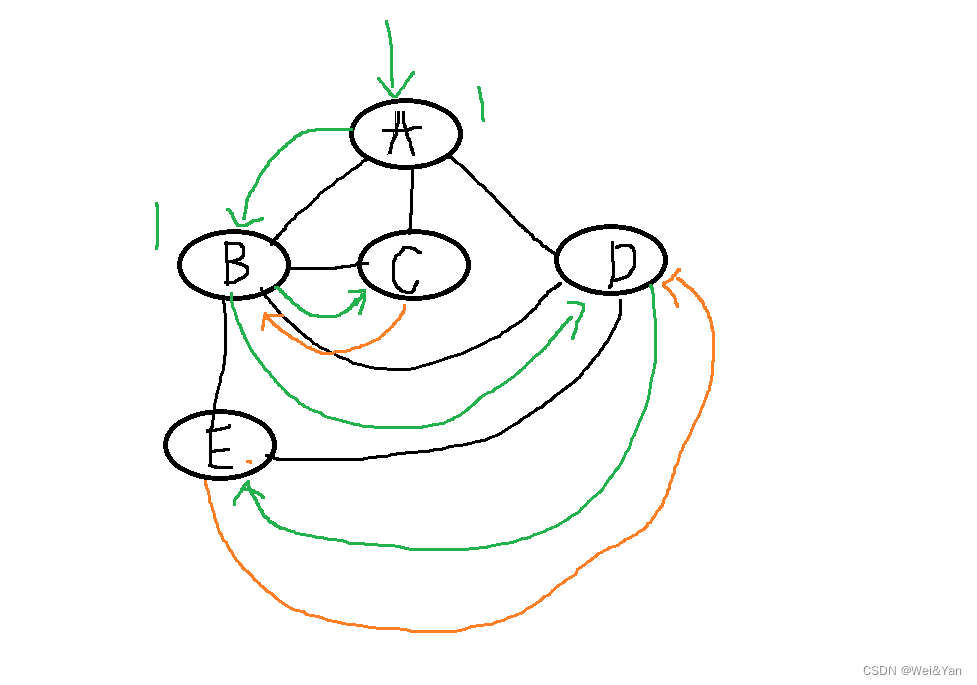
我们先构建一个无向图：如图所示

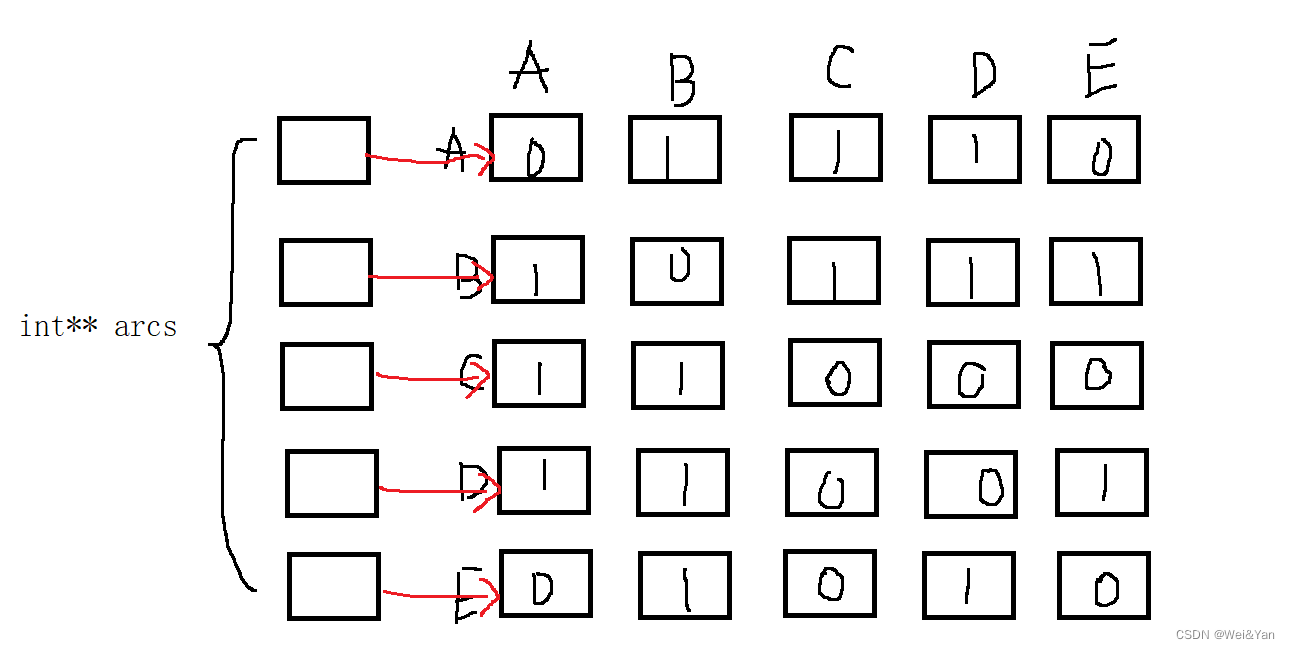
根据规定，如果两个顶点相连，则两顶点的边改为1，否则为0，我们用数组指针arcs来指向标记是否有边的数组。

1.先创建结构体，因为都为动态所以我们都先定义指针再去动态开辟。

2.初始化函数创建结构体后初始化图，将顶点个数传入，开辟空间和初始化顶点和边的信息。

3.创建图函数根据给出的已知各顶点之间边的关系（二维数组）来创建图，传入结构体指针G，顶点，二维数组arts（顶点，边关系），

代码实现：

#include <stdio.h>
#include <stdlib.h>

typedef struct Graph
{
	char* vexs;//顶点
	int** arcs;//边（用二级指针存放存放边的一级指针，一级指针存放边）
	int vexsNum;//顶点的个数
	int arcsNum;//边的个数
}Graph;
//初始化
Graph* initGraph(int vexNum)
{
	Graph* G = (Graph*)malloc(sizeof(Graph));
	G->vexs = (char*)malloc(sizeof(char)*vexNum);
	G->arcs = (int**)malloc(sizeof(int*)*vexNum);
	for (int i = 0; i < vexNum; i++)
	{
		G->arcs[i] = (int*)malloc(sizeof(int) * vexNum);//根据顶点个数开辟n个节点空间
	}
	G->vexsNum = vexNum;//将顶点个数赋值给结构体中的顶点个数
	G->arcsNum = 0;//边个数先初始化为0（初始化的时候不知道图的形状）
	return G;//返回节点
}
//创建
void crativeGraph(Graph* G, char* vexs, int* arcs)
{
	for (int i = 0; i <G->vexsNum; i++)
	{
		G->vexs[i] = vexs[i];//（Graph中的顶点数组存放顶点的“名字”）
	for (int j = 0; j < G->vexsNum; j++)
		{
			G->arcs[i][j] = *(arcs + i * G->vexsNum + j);//根据传进来的二维数组对结构体中的二维数组每个元素赋值（构建树与顶点之间的关系），二维数组加一个数表示第i+1个元素（相当于把二维数组全排成一行）                                                            
			if (G->arcs[i][j] != 0)//两顶点之间有边是则数组元素不为0
				G->arcsNum++;//统计边的个数（二维数组中有边则元素为1）                                                                   
		}
	}
	G->arcsNum /= 2;//（二维数组中对每个顶点都单独统计导致计算了两次边的次数，所以要除2）
}

int main()
{
	Graph* G = initGraph(5);//初始化图

	
	//提前根据图的数创建出符合其边的关系的二位数组
	int arcs[5][5] =
	{
		0,1,1,1,0,
		1,0,1,1,1,
		1,1,0,0,0,
		1,1,0,0,1,
		0,1,0,1,0
	};
	crativeGraph(G, "ABCDE", (int*)arcs);//根据已知二维数组创建图
	return 0;
}

图的深度优先遍历（DFS）：

口诀：一条路走到黑，

不到南墙不回头，

撞墙之后再回头，

回头之后再撞墙。

思路解析：1.找一个节点访问

2.找这个节点可以访问的节点

3.重复第一步直到访问完所有节点

图字结合解析：

根据此图我们绿色：代表访问，橙色代表：相连节点都为已经访问过的节点所以返回上一节点

1.我们构建一个数组visited，作为标记此顶点是否已经被访问（数组大小为顶点个数，初始值都为零，访问过赋值为1）

2.定义下表index：代表每个顶点数组的下表

解析路线：我们传入A，访问A后visited标注为1随机访问（后续我们会图文解释如何随机访问）与A相连的一个顶点如B，访问B后，标注再访问与B相连的顶点C再标记，与C相连的顶点都已经被访问过，于是返回B，访问其他与B相连且没有标记的顶点如访问D再标记，与D相连的E访问再标记。E相连的都被标记，返回D，返回时已经访问完所有顶点。

代码参考：

//DFS深度优先遍历的访问
void DFS(Graph* G, int* visited, int index)
{
	
		printf("%c->", G->vexs[index]);//先打印出顶点
		visited[index] = 1;//再把访问过的顶点做标记
	
	for (int i = 0; i < G->vexsNum; i++)
	{
		if (G->arcs[index][i] == 1 && !visited[i])//当有相连顶点且没有被访问时进入递归
		{
			DFS(G, visited, i);
		}
	}
}
int main()
{
	Graph* G = initGraph(5);
	//创建深度优先遍历的时候判断该顶点是否被访问的数组
	int* visited = (int*)malloc(sizeof(int) * G->vexsNum);
	for (int i = 0; i < G->vexsNum; i++)
	{
		visited[i] = 0;//先把每个元素都设为0，当被访问过的时候就改变元素的值
	}
	//提前根据图的数创建出符合其边的关系的二位数组
	int arcs[5][5] =
	{
		0,1,1,1,0,
		1,0,1,1,1,
		1,1,0,0,0,
		1,1,0,0,1,
		0,1,0,1,0
	};
	crativeGraph(G, "ABCDE", (int*)arcs);
	DFS(G, visited, 0);
	printf("\n");
	return 0;
}

随机访问规律：可以结合下面的图理解我们把index作为结构体中二维数组arcs的行，如访问A后，打印A，将要访问与A相连的顶点再对A所对应的那行一维数组挨个访问，arcs[index][i],index代表第几个顶点，i所代表顶点所对应一维数组的第几个元素，visited代表当前顶点已经被访问。

A的第一个元素为A，arcs[][]为0不符合，挨个往后访问判断第二个元素为B相连，且A已经被访问则递归访问B此时递归的元素index已经变成i，因为要访问第二个顶点B，B在顶点数组vexs中下标为1且i已经++后i=1。以此类推在对B所对应的一维数组判断…………。