CONTENTS
- 一、Python入门
- 1.1 NumPy
- 1.2 Matplotlib
- 二、感知机
- 2.1 感知机是什么
- 2.2 简单逻辑电路
- 2.3 感知机的实现
- 2.4 感知机的局限性
- 2.5 多层感知机
一、Python入门
1.1 NumPy
在深度学习的实现中,经常出现数组和矩阵的计算。NumPy的数组类(numpy.array)中提供了很多便捷的方法,在实现深度学习时,我们将使用这些方法。安装各种第三方库的方式详见:VS Code中安装Python机器学习与数据分析相关第三方模块教程。
导入NumPy:
import numpy as np
生成NumPy数组:
x = np.array([1.0, 2.0, 3.0])
print(x) # [1. 2. 3.]
NumPy数组算术运算:
x = np.array([1.0, 2.0, 3.0])
y = np.array([2.0, 4.0, 6.0])
x + y # [3. 6. 9.]
x - y # [-1. -2. -3.]
x * y # [2. 8. 18.]
x / y # [0.5 0.5 0.5]
x / 2.0 # [0.5 1. 1.5],广播功能
多维NumPy数组:
A = np.array([[1, 2], [3, 4]])
A.shape # (2, 2),查看A的形状
A.dtype # dtype('int64'),查看矩阵元素的数据类型
广播功能如下图所示:


访问矩阵元素的方式:
X = np.array([[51, 55], [14, 19], [0, 4]])
X[0] # array([51, 55]),第0行
X[0][1] # 55,(0, 1)位置的元素
X = X.flatten() # 将X转换为一维数组
print(X) # [51 55 14 19 0 4]
X[np.array([0, 2, 4])] # array([51, 14, 0]),获取索引为0、2、4的元素
从 X X X中抽取大于 15 15 15的元素:
X > 15 # array([True, True, False, True, False, False], dtype=bool)
X[X > 15] # array([51, 55, 19])
1.2 Matplotlib
在深度学习的实验中,图形的绘制和数据的可视化非常重要。Matplotlib是用于绘制图形的库,使用Matplotlib可以轻松地绘制图形和实现数据的可视化。
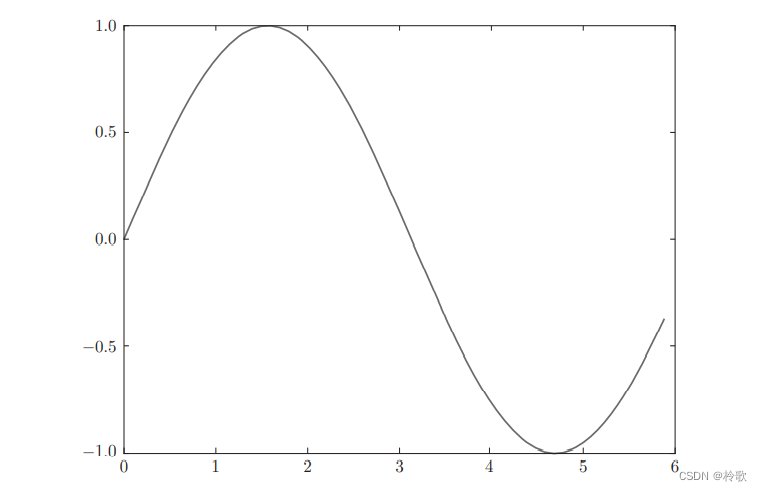
绘制 s i n sin sin函数图像:
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
x = np.arange(0, 6, 0.1) # 以0.1为步长,生成[0, 6)的数据
y = np.sin(x)
# 绘制图形
plt.plot(x, y)
plt.show()
绘制结果如下图所示:
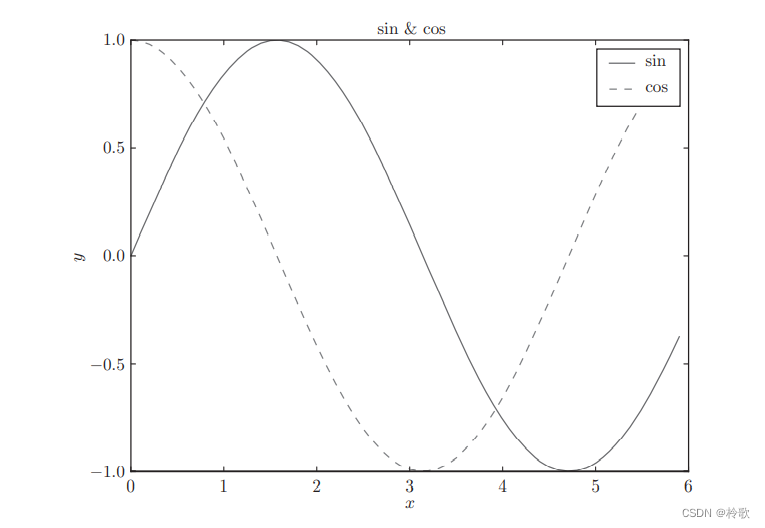
添加 c o s cos cos函数,并添加标题和 x x x轴标签名等其他功能:
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
x = np.arange(0, 6, 0.1) # 以0.1为步长,生成[0, 6)的数据
y1 = np.sin(x)
y2 = np.cos(x)
# 绘制图形
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle="--", label="cos") # 用虚线绘制
plt.xlabel("x") # x轴标签
plt.ylabel("y") # y轴标签
plt.title('sin & cos') # 标题
plt.legend()
plt.show()
绘制结果如下图所示:
pyplot中还提供了用于显示图像的方法imshow()。另外,可以使用matplotlib.image模块的imread()方法读入图像:
import matplotlib.pyplot as plt
from matplotlib.image import imread
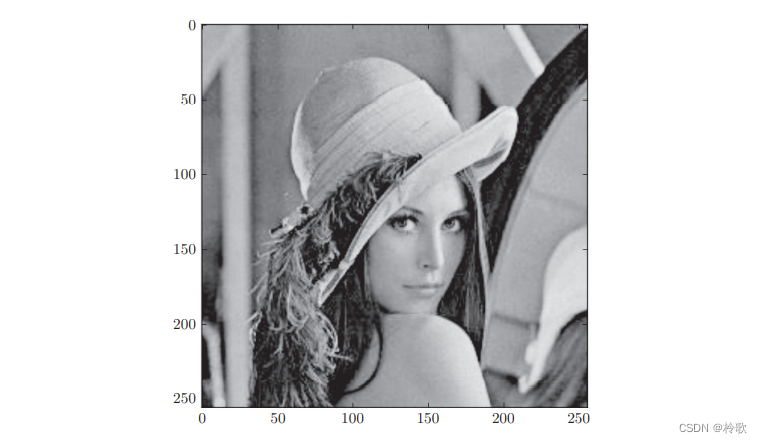
img = imread('lena.png') # 读入图像(设定合适的路径!这里假定图像lena.png在当前目录下)
plt.imshow(img)
plt.show()
运行上述代码后会显示下图所示的图像:
二、感知机
2.1 感知机是什么
感知机接收多个输入信号,输出一个信号。下图是一个接收两个输入信号的感知机的例子, x 1 , x 2 x_1,x_2 x1,x2是输入信号, y y y是输出信号, w 1 , w 2 w_1,w_2 w1,w2是权重( w w w是 w e i g h t weight weight的首字母)。图中的圆圈称为“神经元”或者“节点”。输入信号被送往神经元时,会被分别乘以固定的权重( w 1 x 1 , w 2 x 2 w_1x_1,w_2x_2 w1x1,w2x2)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出 1 1 1。这也称为“神经元被激活”。这里将这个界限值称为阈值,用符号 θ \theta θ表示。
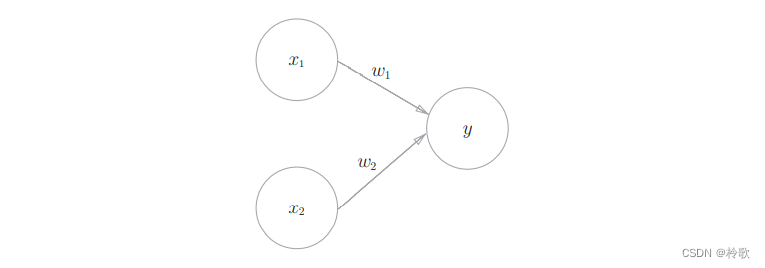
把上述内容用数学式来表示就如下式所示:
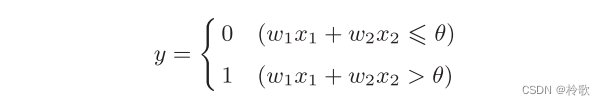
感知机的多个输入信号都有各自固有的权重,这些权重发挥着控制各个信号的重要性的作用。也就是说,权重越大,对应该权重的信号的重要性就越高。
2.2 简单逻辑电路
现在考虑使用感知机来实现 A N D g a t e AND\ gate AND gate,其真值表如下图所示:
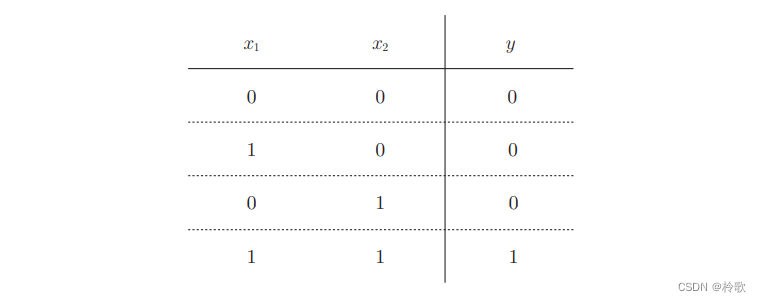
满足上图条件的参数的选择方法有无数多个。当 ( w 1 , w 2 , θ ) = ( 0.5 , 0.5 , 0.7 ) (w_1,w_2,\theta )=(0.5,0.5,0.7) (w1,w2,θ)=(0.5,0.5,0.7)时,可以满足上图条件。设定这样的参数后,仅当 x 1 x_1 x1和 x 2 x_2 x2同时为 1 1 1时,信号的加权总和才会超过给定的阈值 θ \theta θ。
2.3 感知机的实现
用Python来实现上述的逻辑电路:
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
我们将之前数学式中的 θ \theta θ换成 − b -b −b,便可用以下式子表示感知机:
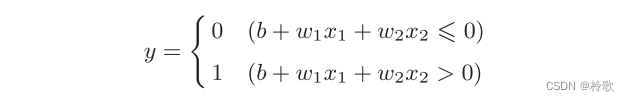
此处, b b b称为偏置, w 1 w_1 w1和 w 2 w_2 w2称为权重。感知机会计算输入信号和权重的乘积,然后加上偏置,如果这个值大于 0 0 0则输出 1 1 1,否则输出 0 0 0。
使用权重和偏置,可以像下面这样实现与门:
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
请注意,偏置和权重 w 1 , w 2 w_1,w_2 w1,w2的作用是不一样的。具体地说, w 1 w_1 w1和 w 2 w_2 w2是控制输入信号的重要性的参数,而偏置是调整神经元被激活的容易程度(输出信号为 1 1 1的程度)的参数。
2.4 感知机的局限性
X O R g a t e XOR\ gate XOR gate真值表如下图所示:
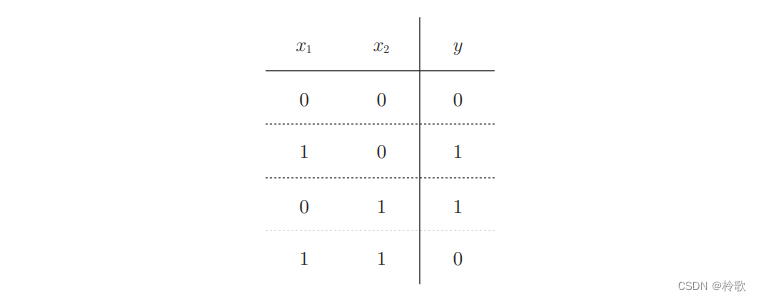
用前面介绍的感知机是无法实现这个异或门的。以或门为例,当权重参数 ( b , w 1 , w 2 ) = ( − 0.5 , 1.0 , 1.0 ) (b,w_1,w_2)=(-0.5,1.0,1.0) (b,w1,w2)=(−0.5,1.0,1.0)时,可满足其真值表条件,此时感知机可用下式表示:
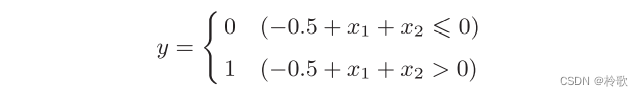
此时感知机会生成由直线 − 0.5 + x 1 + x 2 = 0 -0.5+x_1+x_2=0 −0.5+x1+x2=0分割开的两个空间。其中一个空间输出 1 1 1,另一个空间输出 0 0 0,如下图所示:
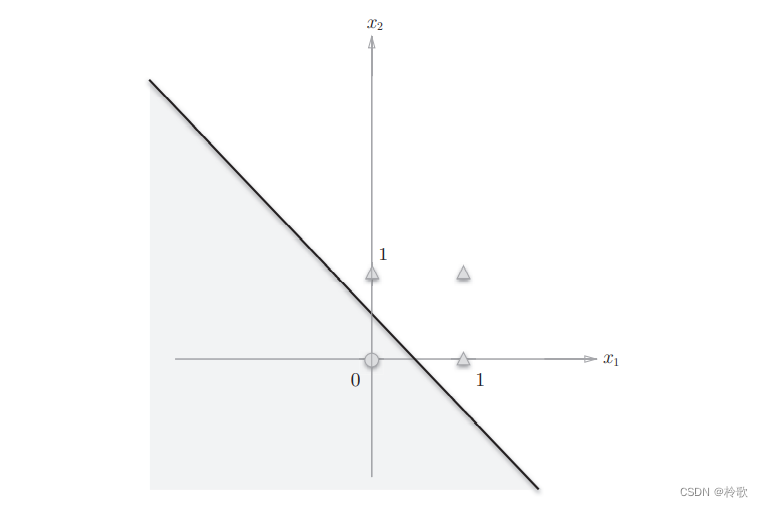
或门在 ( x 1 , x 2 ) = ( 0 , 0 ) (x_1,x_2)=(0,0) (x1,x2)=(0,0)时输出 0 0 0,在 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)为 ( 0 , 1 ) , ( 1 , 0 ) , ( 1 , 1 ) (0,1),(1,0),(1,1) (0,1),(1,0),(1,1)时输出 1 1 1。上图中,圆圈表示 0 0 0,三角形表示 1 1 1。
异或门的输出如下图所示:
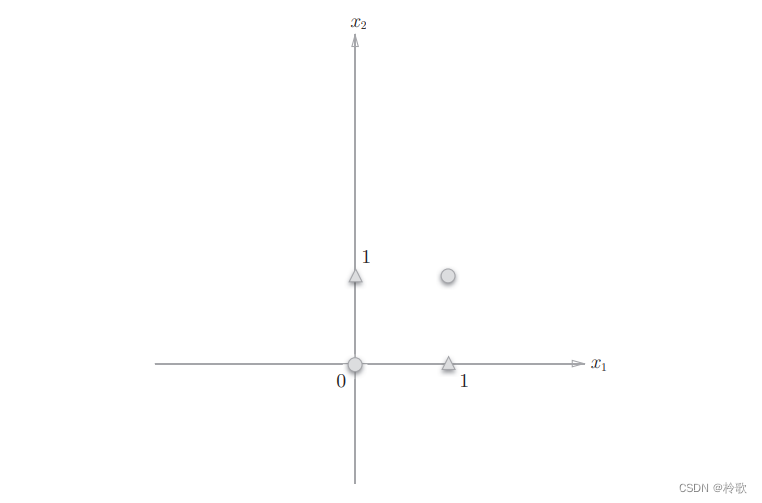
想要用一条直线将上图中的圆圈和三角形分开,无论如何都做不到。
使用曲线分割成的非线性空间即可实现以上条件:
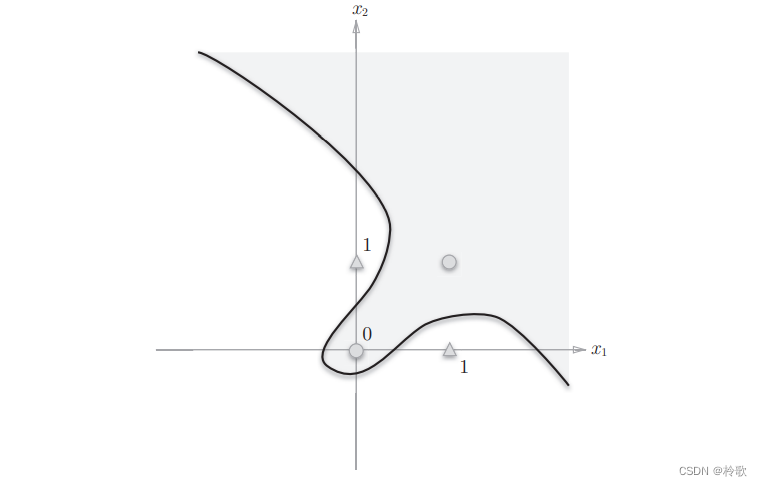
2.5 多层感知机
感知机的绝妙之处在于它可以“叠加层”。异或门可以通过与门、与非门和或门组合进行实现,如下图所示:

假设这三种门均已实现,那么用Python实现异或门的代码如下:
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
下面我们试着用感知机的表示方法(明确地显示神经元)来表示这个异或门,如下图所示,异或门是一种多层结构的神经网络。这里,将最左边的一列称为第 0 0 0层,中间的一列称为第 1 1 1层,最右边的一列称为第 2 2 2层。
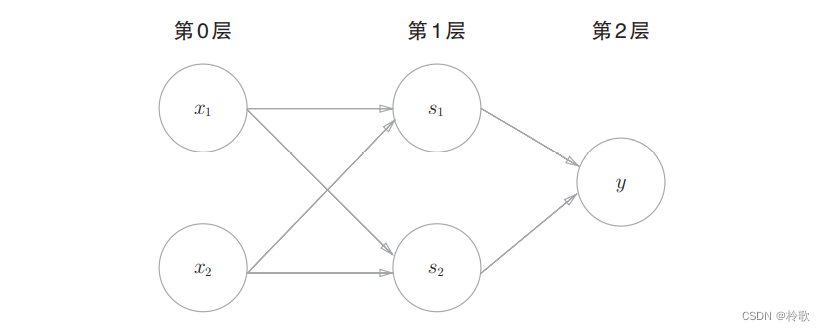
下一节:【学习笔记】深度学习入门:基于Python的理论与实现-神经网络。



![[附源码]计算机毕业设计springboot求职招聘网站](https://img-blog.csdnimg.cn/b582d5a6360a4cea8e423bbaed788690.png)


![[附源码]JAVA毕业设计个人饮食营养管理信息系统(系统+LW)](https://img-blog.csdnimg.cn/7f909163276a4fa7a22c434633888c8c.png)