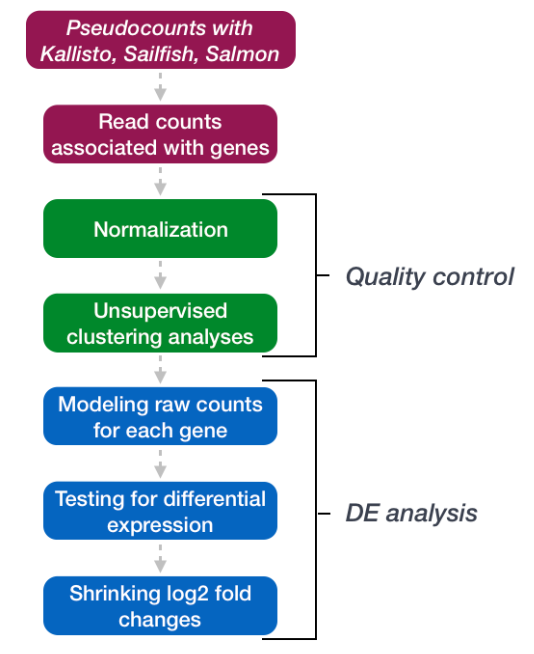
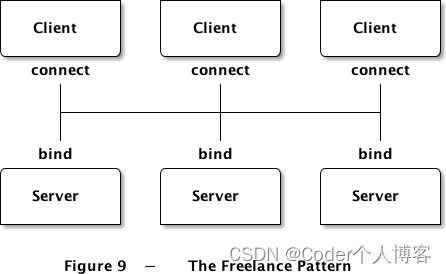
现在很多硬盘采用同密度盘片,意味着内外磁道上的扇区数量不同,扇区数量增加,容量增加,3D很难定位寻址,出现了新的寻址模式:LBA(Logical Block Addressing)。在LBA地址中,地址不再表示实际硬盘的实际物理地址(柱面、磁头和扇区)。LBA编址方式将CHS这种三维寻址方式转变为一维的线性寻址,它把硬盘所有的物理扇区的C/H/S编号通过一定的规则转变为一线性的编号,系统效率得到大大提高,避免了烦琐的磁头/柱面/扇区的寻址方式。在访问硬盘时,由硬盘控制器再将这种逻辑地址转换为实际硬盘的物理地址。
逻辑区块地址LBA是描述电脑存储设备上资料所在区块的通用机制,一般用在像硬盘这样的辅助记忆设备。LBA可以意指某个资料区块的地址或是某个地址所指向的资料区块。现今电脑上所谓一个逻辑区块通常是512或1024位组。ISO-9660格式的标准CD则以2048位组为一个逻辑区块大小。
LBA是非常单纯的一种寻址模式﹔从0开始编号来定位扇区,第一扇区LBA=0,第二扇区LBA=1,依此类推。这种寻址模式取代了原先操作系统必须面对存储设备硬件构造的方式。最具代表性的首推CHS(cylinders-heads-sectors,磁柱-磁头-扇区)寻址模式,区块必须以硬盘上某个磁柱、磁头、扇区的硬件位置所合成的地址来指定。
注意:CHS中的S表示扇区编号,指的是一个磁道中的扇区号,1-63。
LBA寻址使用的为逻辑地址(所有扇区统一编号),CHS寻址使用的物理地址(柱面、磁头和扇区)。
LBA地址和CHS地址转换公式:
LBA(逻辑扇区号)=磁头数 × 每磁道扇区数 × 当前所在柱面号 + 每磁道扇区数 × 当前所在磁头号 + 当前所在扇区号 – 1
注意:对于老式磁盘,每个磁道扇区数量相同。对于新式磁盘,每个磁道扇区数不同。上述计算公式仅适用于老式磁盘。对于新式磁盘,由于每个磁道中扇区数不等,因此需要按实际情况进行类似寻址转换。
新式磁盘采用ZBR(Zone Bit Recording, 等密度记录)的方式组织磁盘介质。
举例:CHS=0/0/1,则根据公式LBA=255 × 63 × 0 + 63 × 0 + 1 – 1= 0
也就是说物理0柱面0磁头1扇区,是逻辑0扇区。
解析:
磁头数 × 每磁道扇区数 × 当前所在柱面号:表示(0~磁头号-1)的所有柱面空间,单位是扇区。
每磁道扇区数 × 当前所在磁头号:表示磁头号所在的柱面中使用的完整的磁道空间,单位是扇区。
当前所在扇区号 – 1:表示磁头号所在磁道中使用的扇区数。由于LBA编号从0开始、磁道扇区编号从1开始,因此需要减1。
LBA编号从0开始。
磁道扇区编号从1开始。
柱面编号从0开始。
磁头编号从0开始。
LBA与C/H/S 之间的转换:
设NS为每磁道扇区数,NH为磁头数,C、H、S分别表示磁盘的柱面、磁头和扇区编号,LBA表示逻辑扇区号,div为整除计算,mod为求余计算,则:
LBA=NH×NS×C+NS×H+S-1;
C=(LBA div NS)div NH;
H=(LBA div NS)mod NH;
S=(LBA mod NS)+1。
对于一块硬盘,扇区个数 = 柱面数 x 磁头数 x 磁道扇区数,即LBA = C x H x S,因此C = LBA / S / H。
LBA div NS表示磁道的总个数,一个柱面包含NH个磁道,因此(LBA div NS)div NH表示柱面数,柱面数从0开始编号,因此无需加1。
LBA div NS表示磁道的总个数,一个柱面包含NH个磁道,因此(LBA div NS)mod NH表示最后剩余的磁头数,磁头编号从0开始,因此无需加1。
LBA就是扇区的总个数,NS表示一个磁道上的扇区数,LBA mod NS就表示剩余的扇区数,扇区从1开始编号,因此此处需要加1。
在磁盘控制器中,有个CHS与LBA的地址转换器,以提供操作系统进行LBA寻址对磁盘操作。

[root@VM_0_15_centos ~]# fdisk -l
Disk /dev/vda: 53.7 GB, 53687091200 bytes
255 heads, 63 sectors/track, 6527 cylinders
Units = cylinders of 16065 * 512 = 8225280 bytes
Sector size (logical/physical): 512 bytes / 512 bytes
I/O size (minimum/optimal): 512 bytes / 512 bytes
Disk identifier: 0x00086547
为什么磁头数为单数?
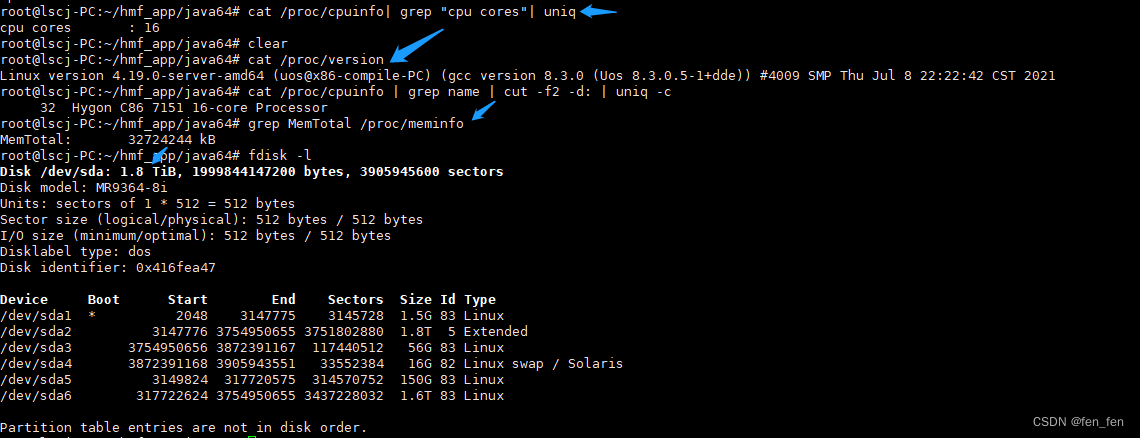
这里不是真实的磁头数,只是为了在LBA换算成CHS时均用了CHS的最大值来转换运算而已。如上面截图一块东芝3T的盘就是 8个盘面 16个磁头数。
磁道外圈与内圈周长 相差巨大,为什么扇区数一样? 且为什么是 63 ?
同理63也不是真实是这样,真实情况肯定是外圈扇区数比内圈大。
为什么我们实际计算的53686402560 bytes数 与 53687091200 bytes不相等?
这个个人是这样理解:Units = cylinders of 16065 512 = 8225280 bytes
CHS的一个最小计算单元,即一1个柱面所拥有的扇区数: 255 * 63 = 16065
那么在LBA上表示出CHS时肯定以LBA为准,CHS作为参考。为此当有零头数时,就直接去掉不在CHS上做显示处理。实际情况中LBA总扇区数几乎一定不是 16065的倍数,所以我们用CHS去计算总大小时会比LBA的值稍小一点。范围是在(1~16064) * 512

![[附源码]计算机毕业设计springboot求职招聘网站](https://img-blog.csdnimg.cn/b582d5a6360a4cea8e423bbaed788690.png)


![[附源码]JAVA毕业设计个人饮食营养管理信息系统(系统+LW)](https://img-blog.csdnimg.cn/7f909163276a4fa7a22c434633888c8c.png)