目录

 编辑距离算法：

步骤：

实例：

题：

完整代码如下：

调试：

代码解析：

具体过程参考： 

 编辑距离算法：

       是一种计算两个自符串之间差异程度的方法，它通过比较两个字符串之间的插入，删除和

替换操作的数量，来确定他们之间的距离。

步骤：

假设我们要将字符串s1转换成另一个字符串s2 。

编辑距离算法通过计算以下三种操作的数量来确定所需的最小变换步骤数：

插入（Insertion）操作：在字符串s1中插入一个字符，以使其与s2一致。

删除（Deletion）操作：从字符串s1中删除一个字符，以使其与s2一致。

替换（Substitution）操作：将字符串s1中的一个字符替换为另一个字符，以使其与s2一致。

实例：

字符串s1:  "CTGA"

字符串s2:   "ACGCTA"

字符串s1得到字符串s2 需要通过如下操作

1.  在字符串s1的C前插入A    ----------"ACTGA"

2.  在"ACTGA"字符串中，将T删除 ----------"ACGA"

3.  在"ACGA"字符G和A中插入C ----------"ACGCA"

4.  在"ACGCA"字符C和A中插入T----------"ACGCTA"

综上：字符串s1得到字符串s2至少花了4个步骤，因此字符串是s1与字符串s2之间的

编辑距离为4

题：

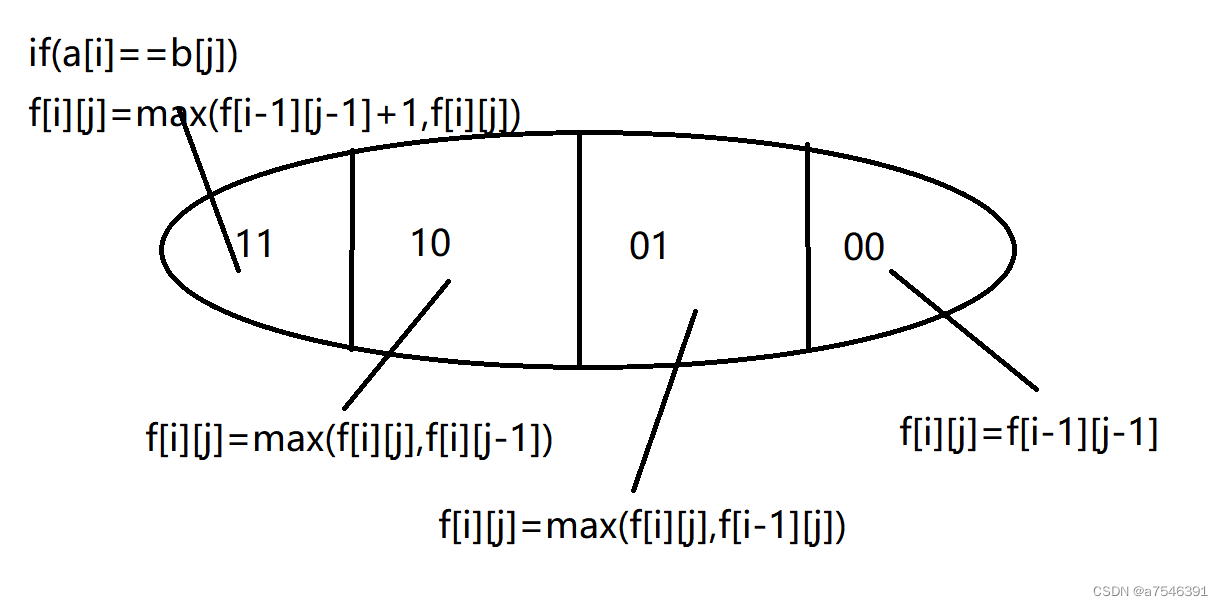
    生物学上通常采用编辑距离来定义两个物种DNA序列的相似性，从而刻画物种之间的进化关系。具体来说，编辑距离是指将一个字符串变换为另一个字符串所需要的最小操作次数。操作有三种，分别为：插入一个字符、删除一个字符以及将一个字符修改为另一个字符。用字符数组str1和str2分别表示长度分别为len1和len2的字符串，定义二维数组d记录求解编辑距离的子问题最优解，则该二维数组可以递归定义为：
 

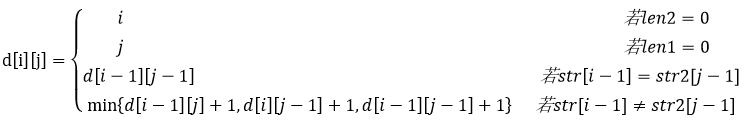
【C代码】
下面是算法的C语言实现。
（1）常量和变量说明
  A，B：两个字符数组
  d：二维数组
  i，j：循环变量
  temp：临时变量
（2）C程序

#include <stdio.h>
#define N 100
char A[N]="CTGA";
char B[N]="ACGCTA";
int d[N][N];
int min(int a, int b){
return a <b ? a: b;
}
int editdistance(char *str1, int len1, char *str2, int len2){
int i, j;
int diff;
int temp;
for(i=0; i<=len1; i++){
d[i][0]=i;
}
for(j=0; j<=len2; j++){
（1） ；
}
for(i=1;i<=len1;i++){
for(j=1; j<=len2; j++){
if( （2） ){
d[i][j]=d[i-1][j-1];
}else{
temp=min(d[i-1][j]+1, d[i][j-1]+1);
d[i][j]=min(temp, （3） );
 }
 }
 }
return （4） ;
}

【问题1】
根据说明和C代码，填充C代码中的空(1)~(4)。

完整代码如下：

#include <stdio.h>

#define N 100

char A[N] = "CTGA";
char B[N] = "ACGCTA";
int d[N][N];

int min(int a, int b){
    return a < b ? a : b;
}

int editdistance(char *str1, int len1, char *str2, int len2){
    int i, j, temp;

    for (i = 0; i <= len1; i++) {
        d[i][0] = i;
    }
    for (j = 0; j <= len2; j++) {
        d[0][j] = j;
    }
    for (i = 1; i <= len1; i++) {
        for (j = 1; j <= len2; j++) {
            if (str1[i - 1] == str2[j - 1]) {
                d[i][j] = d[i - 1][j - 1];
            } else {
                temp = min(d[i - 1][j] + 1, d[i][j - 1] + 1);
                d[i][j] = min(temp, d[i - 1][j - 1] + 1);
            }
        }
    }
    return d[len1][len2];
}

int main() {
    int len1 = 4, len2 = 6;
    printf("Edit distance between %s and %s is %d\n", A, B, editdistance(A, len1, B, len2));
	system("pause");
    return 0;
}

调试：

代码解析：

#include <stdio.h>

#define N 100

char A[N] = "CTGA";
char B[N] = "ACGCTA";

这两行代码分别定义了两个长度为N的字符数组A和B，并初始化为字符串"CTGA"和"ACGCTA
int d[N][N];

这一行代码定义了一个N*N的二维数组d，用于保存计算过程中生成的编辑距离矩阵。

int min(int a, int b){
    return a < b ? a : b;
}

这一段代码定义了一个min的函数，用于计算两个整数的最小值

int editdistance(char *str1, int len1, char *str2, int len2){

这行代码定义了一个名为editdistance的函数，

一个指向字符的指针str1,表示第一个字符串的起始位置

一个整数值len1，表示第一个字符串的长度

一个指向字符的指针str2,表示第二个字符串的起始位置

一个整数值len2，表示第二个字符串的长度

    int i, j, temp;

    for (i = 0; i <= len1; i++) {
        d[i][0] = i;
    }

初始化矩阵第一列
    for (j = 0; j <= len2; j++) {
        d[0][j] = j;
    }

初始化矩阵第一行
    for (i = 1; i <= len1; i++) {
        for (j = 1; j <= len2; j++) {
            if (str1[i - 1] == str2[j - 1]) {

判断字符串str1中的第i个字符（因为数组的指针从0开始，所以i-1表示第i个字符）与

字符串str2中的第j个字符是否相同，如果相同就执行下列语句块。

递归计算矩阵中每个格子的值
                d[i][j] = d[i - 1][j - 1];

具体过程参考：

 https://mp.csdn.net/mp_blog/creation/editor/130600188
         

  } else {
                temp = min(d[i - 1][j] + 1, d[i][j - 1] + 1);
                d[i][j] = min(temp, d[i - 1][j - 1] + 1);

当两字符不同时，取三种操作（增，删，改）的最小值作为距离
            }
        }
    }
    return d[len1][len2];
}

int main() {
    int len1 = 4, len2 = 6;
    printf("Edit distance between %s and %s is %d\n", A, B, editdistance(A, len1, B, len2));
    system("pause");
    return 0;
}

【问题2】
根据说明和C代码，算法采用了(动态规划法)设计策略，时间复杂度为(m*n)(用O符号表示，两个字符串的长度分别用m和n表示)。
【问题3】
已知两个字符串A="CTGA"和B="ACGCTA"，根据说明和C代码，可得出这两个字符串的编辑距离为(4)。