一、题目描述

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。
示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：“bb”

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

二、题目分析&解题思路&代码分析

2.1 常规暴力解法思路

首先分为 3 种情况

1.若 str size 为 1 那么这个 str 肯定是回文字符串
2.若 str size 为 2 那么只需要判断 str[0] 是否等于 str[1] 即可判断是否是回文字符串
3.size 大于等于 3 需要罗列出所有子串的排列组合，然后进行判断是否是子串

思路如下：
在这里插入图片描述
得到全排列结果后，对每个子串进行判断是否是回文串，并记录最长的，时间复杂度是 O(n^3），因为全排列的时间复杂度为 O (n^2) ，再加上判断回文也需要进行头尾挨个进行比较，因此是 O(n^3) 的时间复杂度。

代码示例：

class Solution {
public:
    bool isPalStr(string& s)//判断是否是回文字符串
    {
        if(s.size() == 1)
        {
            return true;
        }
        else if(s.size() == 2)
        {
            return s[0] == s[1];
        }
        else{
            int i = 0;
            int j = s.size()-1;
            while(i < j)//头和尾依次比较
            {
                if(s[i] != s[j])
                {
                    return false;//不相等即不是回文字符串
                }
                i++;
                j--;
            }
            return true;
        }
    }
    string longestPalindrome(string s) {
        string strResult = "";
        int maxsize = 0;
        if(s.size() <= 2)
        {
            if(isPalStr(s))
            {
                return s;
            }
            else
            {
                 strResult +=s[0];
                 return strResult;
            }
        }
        else
        {
            int j = 0;
            int i;
            string str1;
            //获取全排列组合
            while(j < s.size())
            {
                i = j+1;
                str1 = "";
                str1+= s[j];
                while(i<s.size())
                {
                    str1+=s[i];
                    if(isPalStr(str1))//判断是否是回文
                    {
                        if(str1.size() > maxsize)//记录最长的回文字符串
                        {
                            strResult = str1;
                            maxsize = str1.size();
                        }
                    }
                    i++;
                }
                j++;

            }
            if(maxsize == 0)//如果没有 那么任意返回一个字符
            {
                strResult += s[0];
            }
            return strResult;
        }
    }
};

运行结果：可以看到时间复杂度太高了
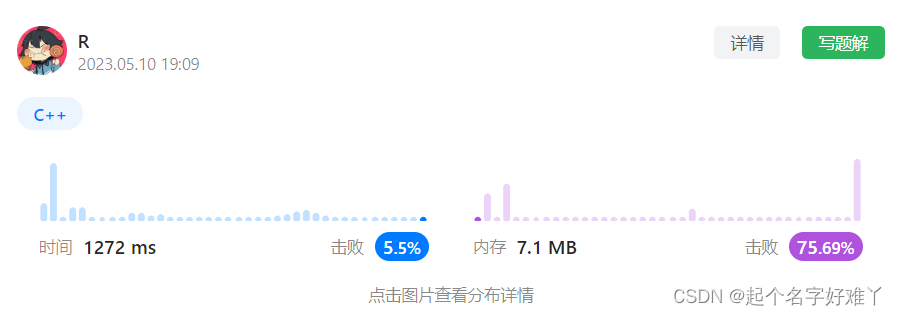
在这里插入图片描述

2.2 构造回文子串法

上述代码复杂度高是因为判断回文子串的时候多了一层循环，那么可不可以将这一层优化掉呢，答案是可以的，就是
不去判断子串是否是回文子串，改为构造出回文子串，直接记录最大长度即可
官方呢给的题解是，中心扩展法，扩展出回文子串，并记录长度。
构造如何构造，如何扩展？且往下看：
说起一个回文子串，无非以下两种情况
1.子串长度为偶数
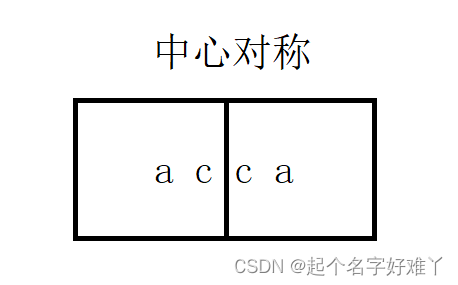
在这里插入图片描述
2.子串长度为奇数

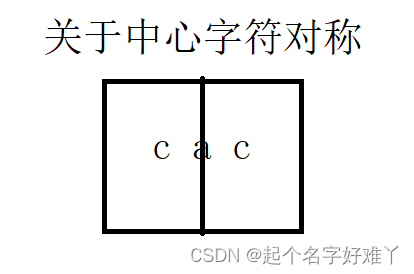
无非就是这两种情况，当然这里谈论的是字符串长度大于 2 的情况
因此我们可以开辟一种新的思路:
1.选定一个字符 x
2.按照以上两种对称方式，分别向该字符x 的左右遍历，遍历左右是否相等，若相等，说明是回文子串，并记录最大长度，最终获取最左边位置与最大长度，即可获取最长的一个回文子串

图示为：
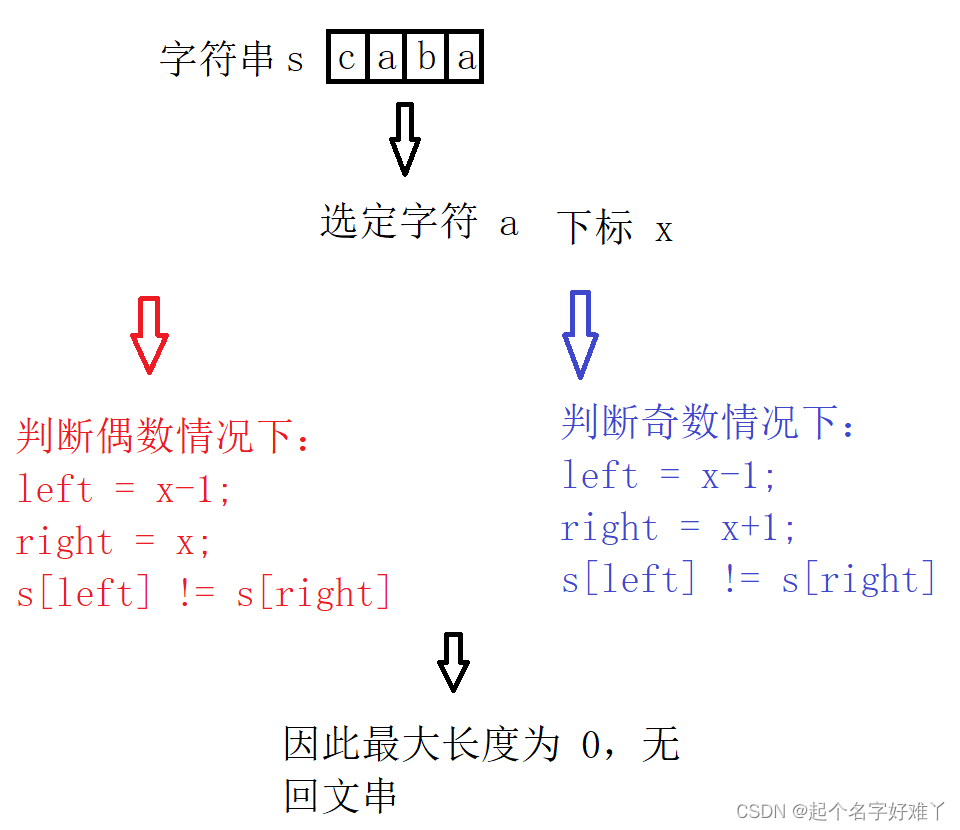
在这里插入图片描述
继续遍历下一个位置的字符

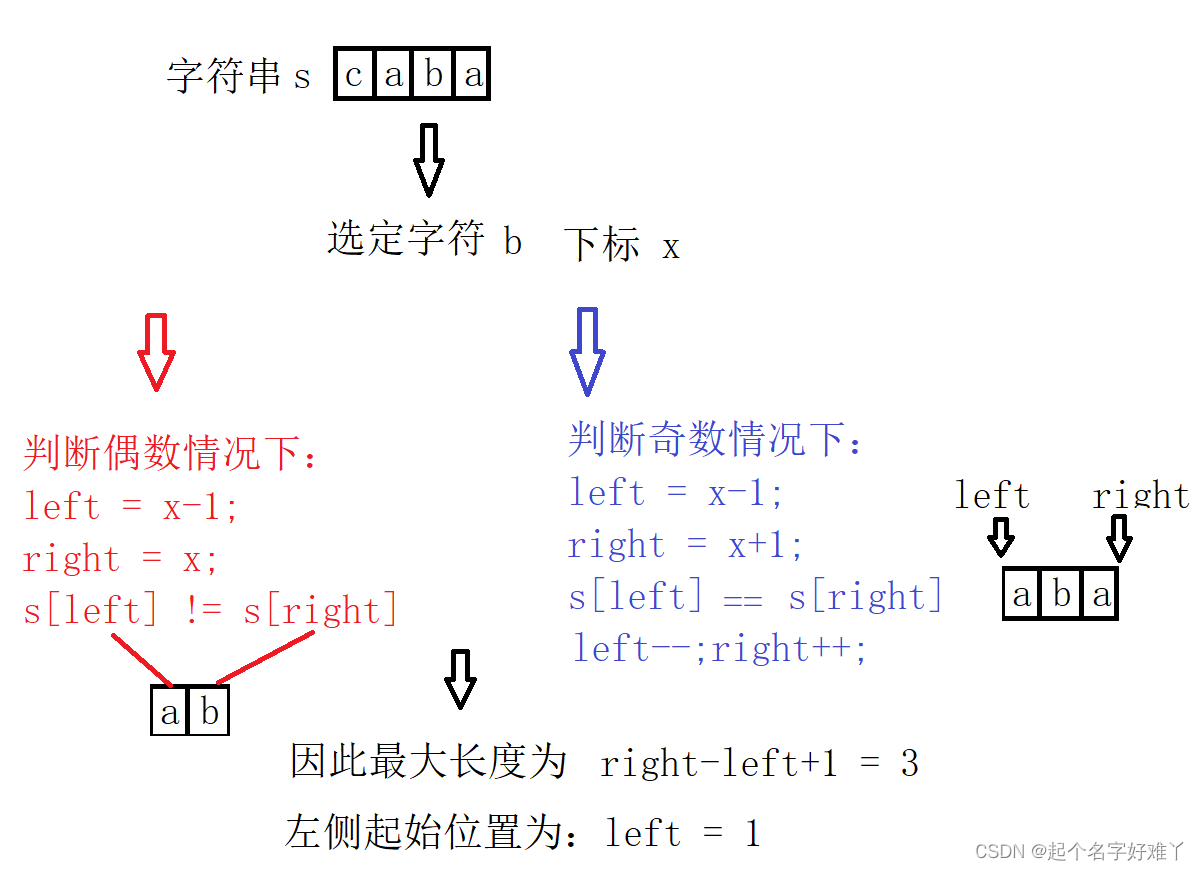
当然也有可能整个字符串没有一个重复的字符，最大长度依然为 0 那么我们只需要任意返回一个字符即可(返回第一个就行)
代码示例：

class Solution {
public:
    string longestPalindrome(string s) {
        int maxLeft = 0;//记录最长回文串的左边起始位置
        int maxSize = 0;//记录最长回文串的长度
        if(s.size() <= 1)
        {
            return s;
        }
        else
        {
            int left = 0;
            int right = 0;
            for(int i = 1; i < s.size();i++)
            {
                left = i-1;
                right = i;
                //当回文串长度为 偶数时(中心对称)
                while(left>=0 && right<s.size() && s[left] == s[right])//注意边界值
                {
                    if(maxSize < right-left+1)//记录较长的回文字符串长度以及左侧起始位置
                    {
                        maxSize = right-left+1;
                        maxLeft = left;
                    }
                    --left;
                    ++right;
                }
                //当回文串长度为奇数时(中心字符是关于s[i]对称)
                left = i-1;
                right = i+1;
                while(left>=0 && right < s.size() && s[left] == s[right])
                {
                    if(maxSize < right-left+1)
                    {
                        maxSize = right-left+1;
                        maxLeft = left;
                    }
                    --left;
                    ++right;
                }
            }
            
        }
        if(maxSize == 0)//没有重复的字符，任意返回一个
        {
            string strTemp = "";
            strTemp += s[0];
            return strTemp;
        }
        else
        {
            //从起始位置截取maxSize 即可
            return s.substr(maxLeft, maxSize);
        }
        
    }
};